 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
变分推断 (VI) 将近似贝叶斯推断视为一个优化问题,并寻求一个“替代”后验分布,该分布最小化与真实后验的 KL 散度。基于梯度的 VI 通常比 MCMC 方法更快,它与模型参数的优化自然地组合在一起,并提供模型证据的下界,该下界可以直接用于模型比较、收敛诊断和可组合推断。
TensorFlow Probability 提供了用于快速、灵活和可扩展的 VI 的工具,这些工具自然地适合 TFP 堆栈。这些工具使能够构建具有由线性变换或归一化流引起的协方差结构的替代后验。
VI 可用于估计回归模型参数的贝叶斯 可信区间,以估计各种治疗或观察到的特征对感兴趣结果的影响。可信区间根据参数的后验分布(以观察到的数据为条件,并假设参数的先验分布)以一定概率对未观察到的参数的值进行界定。
在本 Colab 中,我们演示了如何使用 VI 为贝叶斯线性回归模型的参数获得可信区间,该模型用于测量房屋中的氡含量(使用 Gelman 等人 (2007) 的氡数据集;参见 Stan 中的类似示例)。我们演示了如何将 TFP JointDistribution 与 bijectors 结合起来构建和拟合两种类型的表达性替代后验
- 由块矩阵变换的标准正态分布。该矩阵可以反映后验某些分量之间的独立性和其他分量之间的依赖性,从而放宽了对均值场或全协方差后验的假设。
- 更复杂、更高容量的 逆自回归流。
替代后验经过训练,并与均值场替代后验基线的结果以及来自哈密顿蒙特卡罗的真实样本进行比较。
贝叶斯变分推断概述
假设我们有以下生成过程,其中 \(\theta\) 表示随机参数,\(\omega\) 表示确定性参数,\(x_i\) 是特征,\(y_i\) 是 \(i=1,\ldots,n\) 个观察数据点的目标值:\begin{align} &\theta \sim r(\Theta) && \text{(先验)}\ &\text{for } i = 1 \ldots n: \nonumber \ &\quad y_i \sim p(Y_i|x_i, \theta, \omega) && \text{(似然)} \end{align}
然后 VI 的特征在于:$\newcommand{\E}{\operatorname{\mathbb{E} } } \newcommand{\K}{\operatorname{\mathbb{K} } } \newcommand{\defeq}{\overset{\tiny\text{def} }{=} } \DeclareMathOperator*{\argmin}{arg\,min}$
\begin{align} -\log p({y_i}_i^n|{x_i}_i^n, \omega) &\defeq -\log \int \textrm{d}\theta\, r(\theta) \prod_i^n p(y_i|x_i,\theta, \omega) && \text{(非常难的积分)}\ &= -\log \int \textrm{d}\theta\, q(\theta) \frac{1}{q(\theta)} r(\theta) \prod_i^n p(y_i|x_i,\theta, \omega) && \text{(乘以 1)}\ &\le - \int \textrm{d}\theta\, q(\theta) \log \frac{r(\theta) \prod_i^n p(y_i|xi,\theta, \omega)}{q(\theta)} && \text{(詹森不等式)}\ &\defeq \E{q(\Theta)}[ -\log p(y_i|x_i,\Theta, \omega) ] + \K[q(\Theta), r(\Theta)]\ &\defeq \text{预期负对数似然"} +\text{kl 正则化器"} \end{align}
(从技术上讲,我们假设 \(q\) 相对于 \(r\) 是 绝对连续 的。另请参见 詹森不等式。)
由于该界限对所有 q 都成立,因此对于
\[q^*,w^* = \argmin_{q \in \mathcal{Q},\omega\in\mathbb{R}^d} \left\{ \sum_i^n\E_{q(\Theta)}\left[ -\log p(y_i|x_i,\Theta, \omega) \right] + \K[q(\Theta), r(\Theta)] \right\}\]
关于术语,我们称
- \(q^*\) 为“替代后验”,以及
- \(\mathcal{Q}\) 为“替代族”。
\(\omega^*\) 表示 VI 损失上确定性参数的最大似然值。有关变分推断的更多信息,请参见 这篇综述。
示例:氡测量值的贝叶斯分层线性回归
氡是一种放射性气体,它通过与地面的接触点进入房屋。它是一种致癌物质,是非吸烟者肺癌的主要原因。氡含量在不同家庭之间差异很大。
美国环保署 (EPA) 对 80,000 户住宅的氡气水平进行了研究。两个重要的预测因素是
- 测量所处的楼层(地下室的氡气浓度较高)
- 县级铀含量(与氡气水平呈正相关)
预测按县分组的住宅氡气水平是贝叶斯分层建模中的一个经典问题,由 Gelman 和 Hill (2006) 提出。我们将构建一个分层线性模型来预测住宅的氡气测量值,其中层次结构是按县对住宅进行分组。我们对明尼苏达州住宅氡气水平受位置(县)影响的可信区间感兴趣。为了隔离这种影响,模型中还包括了楼层和铀含量的影响。此外,我们将纳入与按县计算的平均楼层相对应的上下文效应,以便如果测量所处楼层在各县之间存在差异,则不会将其归因于县效应。
pip3 install -q tf-nightly tfp-nightly
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow as tf
import tensorflow_datasets as tfds
import tf_keras
import tensorflow_probability as tfp
import warnings
tfd = tfp.distributions
tfb = tfp.bijectors
plt.rcParams['figure.facecolor'] = '1.'
# Load the Radon dataset from `tensorflow_datasets` and filter to data from
# Minnesota.
dataset = tfds.as_numpy(
tfds.load('radon', split='train').filter(
lambda x: x['features']['state'] == 'MN').batch(10**9))
# Dependent variable: Radon measurements by house.
dataset = next(iter(dataset))
radon_measurement = dataset['activity'].astype(np.float32)
radon_measurement[radon_measurement <= 0.] = 0.1
log_radon = np.log(radon_measurement)
# Measured uranium concentrations in surrounding soil.
uranium_measurement = dataset['features']['Uppm'].astype(np.float32)
log_uranium = np.log(uranium_measurement)
# County indicator.
county_strings = dataset['features']['county'].astype('U13')
unique_counties, county = np.unique(county_strings, return_inverse=True)
county = county.astype(np.int32)
num_counties = unique_counties.size
# Floor on which the measurement was taken.
floor_of_house = dataset['features']['floor'].astype(np.int32)
# Average floor by county (contextual effect).
county_mean_floor = []
for i in range(num_counties):
county_mean_floor.append(floor_of_house[county == i].mean())
county_mean_floor = np.array(county_mean_floor, dtype=log_radon.dtype)
floor_by_county = county_mean_floor[county]
回归模型的具体形式如下
\(\newcommand{\Normal}{\operatorname{\sf Normal} }\) \begin{align} &\text{uranium_weight} \sim \Normal(0, 1) \ &\text{county_floor_weight} \sim \Normal(0, 1) \ &\text{for } j = 1\ldots \text{num_counties}:\ &\quad \text{county_effect}_j \sim \Normal (0, \sigma_c)\ &\text{for } i = 1\ldots n:\ &\quad \mu_i = ( \ &\quad\quad \text{bias} \ &\quad\quad + \text{countyeffect}{\text{county}_i} \ &\quad\quad +\text{log_uranium}_i \times \text{uranium_weight} \ &\quad\quad +\text{floor_of_house}_i \times \text{floor_weight} \ &\quad\quad +\text{floor_bycounty}{\text{county}_i} \times \text{county_floor_weight} ) \ &\quad \text{log_radon}_i \sim \Normal(\mu_i, \sigma_y) \end{align} 其中 \(i\) 表示观测值,\(\text{county}_i\) 表示第 \(i\) 个观测值所在的县。
我们使用县级随机效应来捕捉地理差异。参数 uranium_weight 和 county_floor_weight 是概率建模的,而 floor_weight 和常数 bias 是确定性的。这些建模选择在很大程度上是任意的,是为了演示 VI 在合理复杂性的概率模型上的应用。有关在 TFP 中使用固定效应和随机效应进行多级建模的更深入讨论,以及使用氡气数据集,请参阅 多级建模入门 和 使用变分推断拟合广义线性混合效应模型。
# Create variables for fixed effects.
floor_weight = tf.Variable(0.)
bias = tf.Variable(0.)
# Variables for scale parameters.
log_radon_scale = tfp.util.TransformedVariable(1., tfb.Exp())
county_effect_scale = tfp.util.TransformedVariable(1., tfb.Exp())
# Define the probabilistic graphical model as a JointDistribution.
@tfd.JointDistributionCoroutineAutoBatched
def model():
uranium_weight = yield tfd.Normal(0., scale=1., name='uranium_weight')
county_floor_weight = yield tfd.Normal(
0., scale=1., name='county_floor_weight')
county_effect = yield tfd.Sample(
tfd.Normal(0., scale=county_effect_scale),
sample_shape=[num_counties], name='county_effect')
yield tfd.Normal(
loc=(log_uranium * uranium_weight + floor_of_house* floor_weight
+ floor_by_county * county_floor_weight
+ tf.gather(county_effect, county, axis=-1)
+ bias),
scale=log_radon_scale[..., tf.newaxis],
name='log_radon')
# Pin the observed `log_radon` values to model the un-normalized posterior.
target_model = model.experimental_pin(log_radon=log_radon)
表达能力强的代理后验
接下来,我们使用 VI 和两种不同类型的代理后验来估计随机效应的后验分布
- 受约束的多元正态分布,其协方差结构由分块矩阵变换诱导。
- 由 逆自回归流 变换的多元标准正态分布,然后将其拆分并重构以匹配后验的支持。
多元正态代理后验
为了构建这个代理后验,使用可训练的线性算子来诱导后验分量之间的相关性。
# Determine the `event_shape` of the posterior, and calculate the size of each
# `event_shape` component. These determine the sizes of the components of the
# underlying standard Normal distribution, and the dimensions of the blocks in
# the blockwise matrix transformation.
event_shape = target_model.event_shape_tensor()
flat_event_shape = tf.nest.flatten(event_shape)
flat_event_size = tf.nest.map_structure(tf.reduce_prod, flat_event_shape)
# The `event_space_bijector` maps unconstrained values (in R^n) to the support
# of the prior -- we'll need this at the end to constrain Multivariate Normal
# samples to the prior's support.
event_space_bijector = target_model.experimental_default_event_space_bijector()
构建一个 JointDistribution,其向量值标准正态分量的大小由相应的先验分量决定。这些分量应该是向量值的,以便它们可以被线性算子变换。
base_standard_dist = tfd.JointDistributionSequential(
[tfd.Sample(tfd.Normal(0., 1.), s) for s in flat_event_size])
构建一个可训练的分块下三角线性算子。我们将将其应用于标准正态分布,以实现(可训练的)分块矩阵变换并诱导后验的协方差结构。
在分块线性算子中,可训练的全矩阵块表示后验的两个分量之间的完全协方差,而零块(或 None)表示独立性。对角线上的块要么是下三角矩阵,要么是对角矩阵,因此整个块结构表示一个下三角矩阵。
将此双射器应用于基本分布会导致多元正态分布,其均值为 0,(Cholesky 分解的)协方差等于下三角分块矩阵。
operators = (
(tf.linalg.LinearOperatorDiag,), # Variance of uranium weight (scalar).
(tf.linalg.LinearOperatorFullMatrix, # Covariance between uranium and floor-by-county weights.
tf.linalg.LinearOperatorDiag), # Variance of floor-by-county weight (scalar).
(None, # Independence between uranium weight and county effects.
None, # Independence between floor-by-county and county effects.
tf.linalg.LinearOperatorDiag) # Independence among the 85 county effects.
)
block_tril_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
scale_bijector = tfb.ScaleMatvecLinearOperatorBlock(block_tril_linop)
在将线性算子应用于标准正态分布后,应用一个多部分 Shift 双射器以允许均值取非零值。
loc_bijector = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
通过使用尺度和位置双射器变换标准正态分布获得的结果多元正态分布必须重新整形和重构以匹配先验,最后将其约束到先验的支持。
# Reshape each component to match the prior, using a nested structure of
# `Reshape` bijectors wrapped in `JointMap` to form a multipart bijector.
reshape_bijector = tfb.JointMap(
tf.nest.map_structure(tfb.Reshape, flat_event_shape))
# Restructure the flat list of components to match the prior's structure
unflatten_bijector = tfb.Restructure(
tf.nest.pack_sequence_as(
event_shape, range(len(flat_event_shape))))
现在,将所有内容整合在一起——将可训练的双射器链接在一起,并将它们应用于基本标准正态分布,以构建代理后验。
surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
loc_bijector, # allow for nonzero mean
scale_bijector # apply the block matrix transformation to the standard Normal distribution
]))
训练多元正态代理后验。
optimizer = tf_keras.optimizers.Adam(learning_rate=1e-2)
mvn_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mvn_samples = surrogate_posterior.sample(1000)
mvn_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mvn_samples)
- surrogate_posterior.log_prob(mvn_samples))
print('Multivariate Normal surrogate posterior ELBO: {}'.format(mvn_final_elbo))
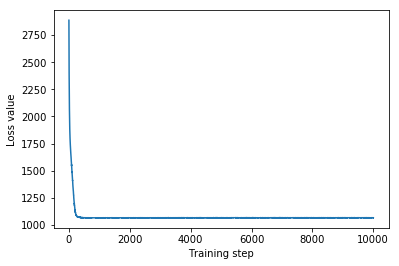
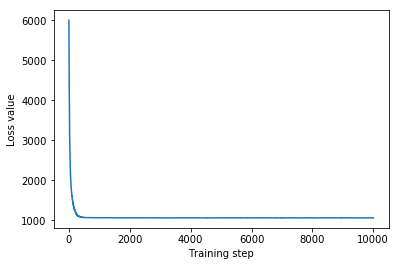
plt.plot(mvn_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Multivariate Normal surrogate posterior ELBO: -1065.705322265625
由于训练后的代理后验是一个 TFP 分布,我们可以从中抽取样本并对其进行处理,以生成参数的后验可信区间。
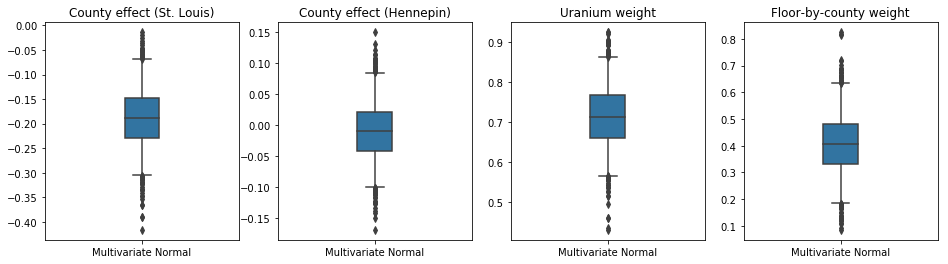
下面的箱线图显示了两个最大县的县效应和土壤铀测量值回归权重以及按县计算的平均楼层的 50% 和 95% 可信区间。县效应的后验可信区间表明,在考虑其他变量后,圣路易斯县的位置与较低的氡气水平相关,而亨内平县的位置效应接近中性。
回归权重的后验可信区间表明,较高的土壤铀含量与较高的氡气水平相关,并且测量值在较高楼层(可能是因为房屋没有地下室)进行的县往往具有较高的氡气水平,这可能与土壤特性及其对建筑类型的影响有关。
(确定性的)楼层系数为负,表明较低的楼层具有较高的氡气水平,正如预期的那样。
st_louis_co = 69 # Index of St. Louis, the county with the most observations.
hennepin_co = 25 # Index of Hennepin, with the second-most observations.
def pack_samples(samples):
return {'County effect (St. Louis)': samples.county_effect[..., st_louis_co],
'County effect (Hennepin)': samples.county_effect[..., hennepin_co],
'Uranium weight': samples.uranium_weight,
'Floor-by-county weight': samples.county_floor_weight}
def plot_boxplot(posterior_samples):
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
# Invert the results dict for easier plotting.
k = list(posterior_samples.values())[0].keys()
plot_results = {
v: {p: posterior_samples[p][v] for p in posterior_samples} for v in k}
for i, (var, var_results) in enumerate(plot_results.items()):
sns.boxplot(data=list(var_results.values()), ax=axes[i],
width=0.18*len(var_results), whis=(2.5, 97.5))
# axes[i].boxplot(list(var_results.values()), whis=(2.5, 97.5))
axes[i].title.set_text(var)
fs = 10 if len(var_results) < 4 else 8
axes[i].set_xticklabels(list(var_results.keys()), fontsize=fs)
results = {'Multivariate Normal': pack_samples(mvn_samples)}
print('Bias is: {:.2f}'.format(bias.numpy()))
print('Floor fixed effect is: {:.2f}'.format(floor_weight.numpy()))
plot_boxplot(results)
Bias is: 1.40 Floor fixed effect is: -0.72
逆自回归流代理后验
逆自回归流 (IAF) 是归一化流,它使用神经网络来捕捉分布分量之间复杂的非线性依赖关系。接下来,我们构建一个 IAF 代理后验,以查看这种容量更大、更灵活的模型是否优于受约束的多元正态。
# Build a standard Normal with a vector `event_shape`, with length equal to the
# total number of degrees of freedom in the posterior.
base_distribution = tfd.Sample(
tfd.Normal(0., 1.), sample_shape=[tf.reduce_sum(flat_event_size)])
# Apply an IAF to the base distribution.
num_iafs = 2
iaf_bijectors = [
tfb.Invert(tfb.MaskedAutoregressiveFlow(
shift_and_log_scale_fn=tfb.AutoregressiveNetwork(
params=2, hidden_units=[256, 256], activation='relu')))
for _ in range(num_iafs)
]
# Split the base distribution's `event_shape` into components that are equal
# in size to the prior's components.
split = tfb.Split(flat_event_size)
# Chain these bijectors and apply them to the standard Normal base distribution
# to build the surrogate posterior. `event_space_bijector`,
# `unflatten_bijector`, and `reshape_bijector` are the same as in the
# multivariate Normal surrogate posterior.
iaf_surrogate_posterior = tfd.TransformedDistribution(
base_distribution,
bijector=tfb.Chain([
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the prior
reshape_bijector, # reshape the vector-valued components to match the shapes of the prior components
split] + # Split the samples into components of the same size as the prior components
iaf_bijectors # Apply a flow model to the Tensor-valued standard Normal distribution
))
训练 IAF 代理后验。
optimizer=tf_keras.optimizers.Adam(learning_rate=1e-2)
iaf_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
iaf_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=4,
jit_compile=True)
iaf_samples = iaf_surrogate_posterior.sample(1000)
iaf_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*iaf_samples)
- iaf_surrogate_posterior.log_prob(iaf_samples))
print('IAF surrogate posterior ELBO: {}'.format(iaf_final_elbo))
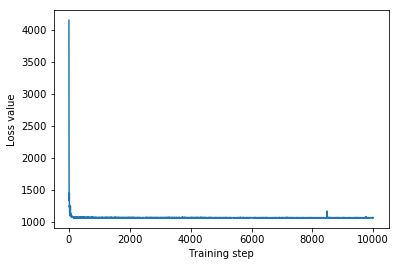
plt.plot(iaf_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
IAF surrogate posterior ELBO: -1065.3663330078125
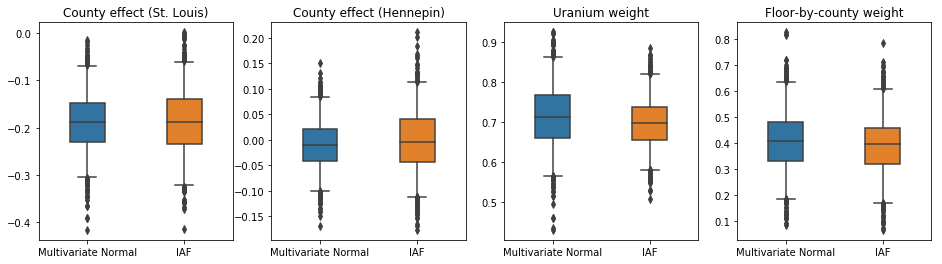
IAF 代理后验的可信区间与受约束的多元正态的可信区间相似。
results['IAF'] = pack_samples(iaf_samples)
plot_boxplot(results)
基线:均值场代理后验
VI 代理后验通常被假定为均值场(独立)正态分布,具有可训练的均值和方差,并通过双射变换约束到先验的支持。我们除了两个更具表达能力的代理后验之外,还定义了一个均值场代理后验,使用与多元正态代理后验相同的通用公式。
# A block-diagonal linear operator, in which each block is a diagonal operator,
# transforms the standard Normal base distribution to produce a mean-field
# surrogate posterior.
operators = (tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag,
tf.linalg.LinearOperatorDiag)
block_diag_linop = (
tfp.experimental.vi.util.build_trainable_linear_operator_block(
operators, flat_event_size))
mean_field_scale = tfb.ScaleMatvecLinearOperatorBlock(block_diag_linop)
mean_field_loc = tfb.JointMap(
tf.nest.map_structure(
lambda s: tfb.Shift(
tf.Variable(tf.random.uniform(
(s,), minval=-2., maxval=2., dtype=tf.float32))),
flat_event_size))
mean_field_surrogate_posterior = tfd.TransformedDistribution(
base_standard_dist,
bijector = tfb.Chain( # Note that the chained bijectors are applied in reverse order
[
event_space_bijector, # constrain the surrogate to the support of the prior
unflatten_bijector, # pack the reshaped components into the `event_shape` structure of the posterior
reshape_bijector, # reshape the vector-valued components to match the shapes of the posterior components
mean_field_loc, # allow for nonzero mean
mean_field_scale # apply the block matrix transformation to the standard Normal distribution
]))
optimizer=tf_keras.optimizers.Adam(learning_rate=1e-2)
mean_field_loss = tfp.vi.fit_surrogate_posterior(
target_model.unnormalized_log_prob,
mean_field_surrogate_posterior,
optimizer=optimizer,
num_steps=10**4,
sample_size=16,
jit_compile=True)
mean_field_samples = mean_field_surrogate_posterior.sample(1000)
mean_field_final_elbo = tf.reduce_mean(
target_model.unnormalized_log_prob(*mean_field_samples)
- mean_field_surrogate_posterior.log_prob(mean_field_samples))
print('Mean-field surrogate posterior ELBO: {}'.format(mean_field_final_elbo))
plt.plot(mean_field_loss)
plt.xlabel('Training step')
_ = plt.ylabel('Loss value')
Mean-field surrogate posterior ELBO: -1065.7652587890625
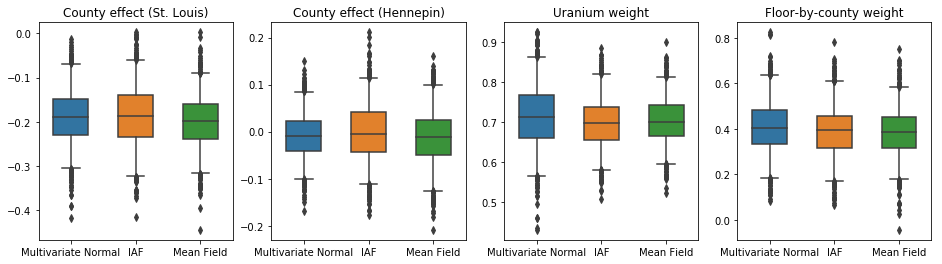
在这种情况下,均值场代理后验给出了与更具表达能力的代理后验相似的结果,表明这种更简单的模型可能足以完成推断任务。
results['Mean Field'] = pack_samples(mean_field_samples)
plot_boxplot(results)
真实值:哈密顿蒙特卡罗 (HMC)
我们使用 HMC 从真实后验中生成“真实值”样本,以与代理后验的结果进行比较。
num_chains = 8
num_leapfrog_steps = 3
step_size = 0.4
num_steps=20000
flat_event_shape = tf.nest.flatten(target_model.event_shape)
enum_components = list(range(len(flat_event_shape)))
bijector = tfb.Restructure(
enum_components,
tf.nest.pack_sequence_as(target_model.event_shape, enum_components))(
target_model.experimental_default_event_space_bijector())
current_state = bijector(
tf.nest.map_structure(
lambda e: tf.zeros([num_chains] + list(e), dtype=tf.float32),
target_model.event_shape))
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_model.unnormalized_log_prob,
num_leapfrog_steps=num_leapfrog_steps,
step_size=[tf.fill(s.shape, step_size) for s in current_state])
hmc = tfp.mcmc.TransformedTransitionKernel(
hmc, bijector)
hmc = tfp.mcmc.DualAveragingStepSizeAdaptation(
hmc,
num_adaptation_steps=int(num_steps // 2 * 0.8),
target_accept_prob=0.9)
chain, is_accepted = tf.function(
lambda current_state: tfp.mcmc.sample_chain(
current_state=current_state,
kernel=hmc,
num_results=num_steps // 2,
num_burnin_steps=num_steps // 2,
trace_fn=lambda _, pkr:
(pkr.inner_results.inner_results.is_accepted),
),
autograph=False,
jit_compile=True)(current_state)
accept_rate = tf.reduce_mean(tf.cast(is_accepted, tf.float32))
ess = tf.nest.map_structure(
lambda c: tfp.mcmc.effective_sample_size(
c,
cross_chain_dims=1,
filter_beyond_positive_pairs=True),
chain)
r_hat = tf.nest.map_structure(tfp.mcmc.potential_scale_reduction, chain)
hmc_samples = pack_samples(
tf.nest.pack_sequence_as(target_model.event_shape, chain))
print('Acceptance rate is {}'.format(accept_rate))
Acceptance rate is 0.9008625149726868
绘制样本轨迹以对 HMC 结果进行健全性检查。
def plot_traces(var_name, samples):
fig, axes = plt.subplots(1, 2, figsize=(14, 1.5), sharex='col', sharey='col')
for chain in range(num_chains):
s = samples.numpy()[:, chain]
axes[0].plot(s, alpha=0.7)
sns.kdeplot(s, ax=axes[1], shade=False)
axes[0].title.set_text("'{}' trace".format(var_name))
axes[1].title.set_text("'{}' distribution".format(var_name))
axes[0].set_xlabel('Iteration')
warnings.filterwarnings('ignore')
for var, var_samples in hmc_samples.items():
plot_traces(var, var_samples)




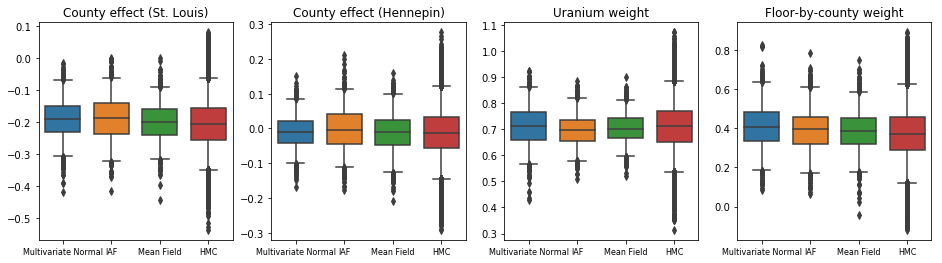
所有三个代理后验都产生了与 HMC 样本在视觉上相似的可信区间,尽管有时由于 ELBO 损失的影响而出现欠分散,这在 VI 中很常见。
results['HMC'] = hmc_samples
plot_boxplot(results)
其他结果
绘图函数
证据下界 (ELBO)
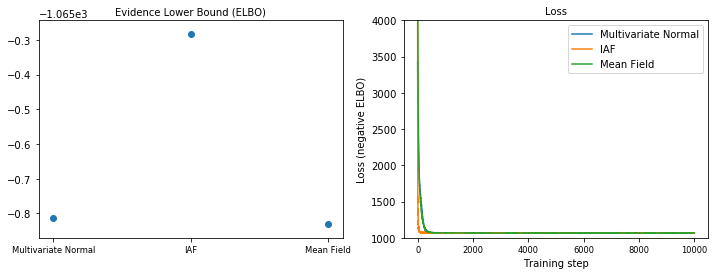
IAF 是迄今为止最大、最灵活的代理后验,它收敛到最高的证据下界 (ELBO)。
plot_loss_and_elbo()
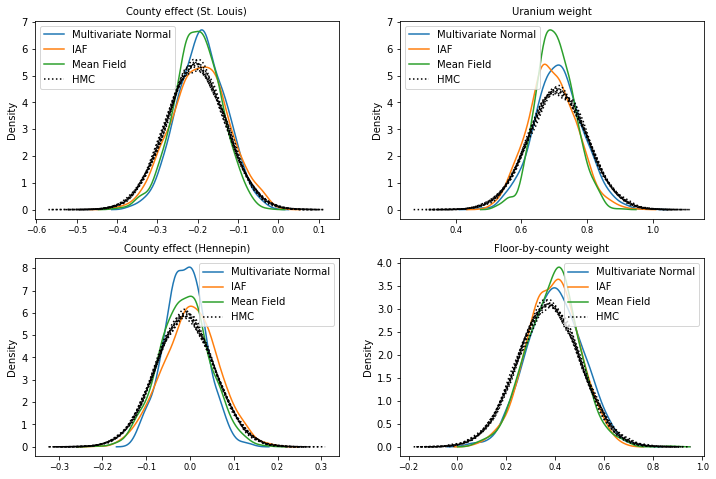
后验样本
来自每个代理后验的样本,与 HMC 真实值样本进行比较(箱线图中显示的样本的不同可视化)。
plot_kdes()
结论
在这个 Colab 中,我们使用联合分布和多部分双射器构建了 VI 代理后验,并对其进行拟合以估计氡气数据集回归模型中权重的可信区间。对于这个简单的模型,更具表达能力的代理后验的性能与均值场代理后验相似。但是,我们演示的工具可用于构建各种灵活的代理后验,适用于更复杂的模型。
