 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
我编写了这个笔记本作为案例研究来学习 TensorFlow Probability。我选择解决的问题是估计二维均值为 0 的高斯随机变量样本的协方差矩阵。这个问题有一些不错的特点
- 如果我们对协方差使用逆 Wishart 先验(一种常见方法),则该问题具有解析解,因此我们可以检查结果。
- 该问题涉及对受约束的参数进行采样,这增加了一些有趣的复杂性。
- 最直接的解决方案不是最快的解决方案,因此需要进行一些优化工作。
我决定在进行过程中记录我的经验。我花了一段时间才理解 TFP 的细微之处,因此这个笔记本从非常简单开始,然后逐渐过渡到更复杂的 TFP 功能。我在过程中遇到了很多问题,我试图捕捉到帮助我识别这些问题以及我最终找到的解决方法。我试图包含 *大量* 的细节(包括大量测试以确保各个步骤是正确的)。
为什么要学习 TensorFlow Probability?
我发现 TensorFlow Probability 对我的项目很有吸引力,原因有以下几点
- TensorFlow Probability 允许您在笔记本中交互式地原型设计和开发复杂模型。您可以将代码分解成可以交互式地和使用单元测试进行测试的小片段。
- 准备好扩展时,您可以利用我们为使 TensorFlow 在多台机器上的多个优化处理器上运行而构建的所有基础设施。
- 最后,虽然我真的很喜欢 Stan,但我发现它很难调试。您必须在独立语言中编写所有建模代码,该语言几乎没有工具可以让您查看代码、检查中间状态等等。
缺点是 TensorFlow Probability 比 Stan 和 PyMC3 新得多,因此文档仍在开发中,还有很多功能尚未构建。令人高兴的是,我发现 TFP 的基础很牢固,并且以模块化方式设计,允许人们相当直接地扩展其功能。在这个笔记本中,除了解决案例研究之外,我还将展示一些扩展 TFP 的方法。
适合人群
我假设读者在阅读这个笔记本时具备一些重要的先决条件。您应该
- 了解贝叶斯推理的基础知识。(如果您不了解,一本非常好的入门书籍是 *统计重思*)
- 熟悉 MCMC 采样库,例如 Stan / PyMC3 / BUGS
- 牢固掌握 NumPy(一本不错的入门书籍是 *Python 数据分析*)
- 至少对 TensorFlow 有基本的了解,但不一定需要精通。(*学习 TensorFlow* 很好,但 TensorFlow 的快速发展意味着大多数书籍都会过时。斯坦福大学的 CS20 课程也很好。)
第一次尝试
这是我对该问题的第一次尝试。剧透:我的解决方案不起作用,需要多次尝试才能使事情变得正确!虽然这个过程需要一段时间,但下面的每次尝试都有助于学习 TFP 的新部分。
注意:TFP 目前没有实现逆 Wishart 分布(我们将在最后看到如何创建自己的逆 Wishart),因此我将把问题改为使用 Wishart 先验估计精度矩阵。
import collections
import math
import os
import time
import numpy as np
import pandas as pd
import scipy
import scipy.stats
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
步骤 1:将观测值收集在一起
这里我的数据都是合成的,因此这看起来比现实世界的例子更整洁。但是,没有理由不能生成您自己的合成数据。
提示:确定模型形式后,可以选择一些参数值并使用所选模型生成一些合成数据。作为实现的健全性检查,您可以验证您的估计值是否包含您选择的参数的真实值。为了使您的调试/测试周期更快,您可以考虑使用模型的简化版本(例如,使用更少的维度或更少的样本)。
提示:最简单的方法是将您的观测值作为 NumPy 数组处理。需要注意的一点是,NumPy 默认使用 float64,而 TensorFlow 默认使用 float32。
通常,TensorFlow 操作希望所有参数具有相同的类型,您需要进行显式数据转换才能更改类型。如果您使用 float64 观测值,则需要添加许多转换操作。相反,NumPy 会自动处理转换。因此,将您的 Numpy 数据转换为 float32 比强制 TensorFlow 使用 float64 容易得多。
选择一些参数值
# We're assuming 2-D data with a known true mean of (0, 0)
true_mean = np.zeros([2], dtype=np.float32)
# We'll make the 2 coordinates correlated
true_cor = np.array([[1.0, 0.9], [0.9, 1.0]], dtype=np.float32)
# And we'll give the 2 coordinates different variances
true_var = np.array([4.0, 1.0], dtype=np.float32)
# Combine the variances and correlations into a covariance matrix
true_cov = np.expand_dims(np.sqrt(true_var), axis=1).dot(
np.expand_dims(np.sqrt(true_var), axis=1).T) * true_cor
# We'll be working with precision matrices, so we'll go ahead and compute the
# true precision matrix here
true_precision = np.linalg.inv(true_cov)
# Here's our resulting covariance matrix
print(true_cov)
# Verify that it's positive definite, since np.random.multivariate_normal
# complains about it not being positive definite for some reason.
# (Note that I'll be including a lot of sanity checking code in this notebook -
# it's a *huge* help for debugging)
print('eigenvalues: ', np.linalg.eigvals(true_cov))
[[4. 1.8] [1.8 1. ]] eigenvalues: [4.843075 0.15692513]
生成一些合成观测值
请注意,TensorFlow Probability 使用以下约定:数据的初始维度表示样本索引,数据的最终维度表示样本的维度。
这里我们想要 100 个样本,每个样本都是一个长度为 2 的向量。我们将生成一个形状为 (100, 2) 的数组 my_data。 my_data[i, :] 是第 \(i\) 个样本,它是一个长度为 2 的向量。
(请记住使 my_data 的类型为 float32!)
# Set the seed so the results are reproducible.
np.random.seed(123)
# Now generate some observations of our random variable.
# (Note that I'm suppressing a bunch of spurious about the covariance matrix
# not being positive semidefinite via check_valid='ignore' because it really is
# positive definite!)
my_data = np.random.multivariate_normal(
mean=true_mean, cov=true_cov, size=100,
check_valid='ignore').astype(np.float32)
my_data.shape
(100, 2)
对观测值进行健全性检查
潜在的错误来源之一是弄乱了您的合成数据!让我们进行一些简单的检查。
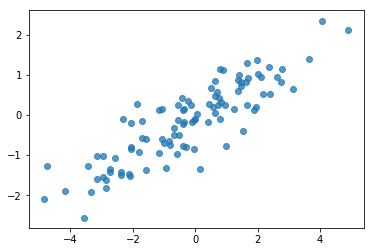
# Do a scatter plot of the observations to make sure they look like what we
# expect (higher variance on the x-axis, y values strongly correlated with x)
plt.scatter(my_data[:, 0], my_data[:, 1], alpha=0.75)
plt.show()
print('mean of observations:', np.mean(my_data, axis=0))
print('true mean:', true_mean)
mean of observations: [-0.24009615 -0.16638893] true mean: [0. 0.]
print('covariance of observations:\n', np.cov(my_data, rowvar=False))
print('true covariance:\n', true_cov)
covariance of observations: [[3.95307734 1.68718486] [1.68718486 0.94910269]] true covariance: [[4. 1.8] [1.8 1. ]]
好的,我们的样本看起来很合理。下一步。
步骤 2:在 NumPy 中实现似然函数
我们需要编写的主要内容是在 TF Probability 中执行 MCMC 采样,即对数似然函数。通常,编写 TF 比 NumPy 稍微棘手一些,因此我发现先在 NumPy 中进行初始实现很有帮助。我将似然函数分成两部分,一个数据似然函数对应于 \(P(data | parameters)\),另一个先验似然函数对应于 \(P(parameters)\)。
请注意,这些 NumPy 函数不必经过超级优化/矢量化,因为目标只是生成一些用于测试的值。正确性是关键考虑因素!
首先,我们将实现数据对数似然部分。这很简单。要记住的一点是,我们将使用精度矩阵,因此我们将相应地进行参数化。
def log_lik_data_numpy(precision, data):
# np.linalg.inv is a really inefficient way to get the covariance matrix, but
# remember we don't care about speed here
cov = np.linalg.inv(precision)
rv = scipy.stats.multivariate_normal(true_mean, cov)
return np.sum(rv.logpdf(data))
# test case: compute the log likelihood of the data given the true parameters
log_lik_data_numpy(true_precision, my_data)
-280.81822950593767
我们将对精度矩阵使用 Wishart 先验,因为后验存在解析解(参见 维基百科中关于共轭先验的便捷表格)。
Wishart 分布 有 2 个参数
- 自由度的数量(在维基百科中标记为 \(\nu\)
- 一个尺度矩阵(在维基百科中标记为 \(V\)
具有参数 \(\nu, V\) 的 Wishart 分布的均值为 \(E[W] = \nu V\),方差为 \(\text{Var}(W_{ij}) = \nu(v_{ij}^2+v_{ii}v_{jj})\)
一些有用的直觉:您可以通过从具有均值 0 和协方差 \(V\) 的多元正态随机变量生成 \(\nu\) 个独立抽取 \(x_1 \ldots x_{\nu}\),然后形成和 \(W = \sum_{i=1}^{\nu} x_i x_i^T\) 来生成 Wishart 样本。
如果您通过除以 \(\nu\) 来重新缩放 Wishart 样本,您将获得 \(x_i\) 的样本协方差矩阵。随着 \(\nu\) 的增加,此样本协方差矩阵应该趋向于 \(V\)。当 \(\nu\) 很小时,样本协方差矩阵存在很大差异,因此 \(\nu\) 的小值对应于较弱的先验,而 \(\nu\) 的大值对应于较强的先验。请注意,\(\nu\) 必须至少与您正在采样的空间的维度一样大,否则您将生成奇异矩阵。
我们将使用 \(\nu = 3\),因此我们有一个弱先验,我们将取 \(V = \frac{1}{\nu} I\),这将使我们的协方差估计值趋向于单位矩阵(回想一下,均值为 \(\nu V\)).
PRIOR_DF = 3
PRIOR_SCALE = np.eye(2, dtype=np.float32) / PRIOR_DF
def log_lik_prior_numpy(precision):
rv = scipy.stats.wishart(df=PRIOR_DF, scale=PRIOR_SCALE)
return rv.logpdf(precision)
# test case: compute the prior for the true parameters
log_lik_prior_numpy(true_precision)
-9.103606346649766
Wishart 分布是估计具有已知均值 \(\mu\) 的多元正态的精度矩阵的共轭先验。
假设先验 Wishart 参数为 \(\nu, V\),并且我们对多元正态有 \(n\) 个观测值,\(x_1, \ldots, x_n\)。后验参数为 \(n + \nu, \left(V^{-1} + \sum_{i=1}^n (x_i-\mu)(x_i-\mu)^T \right)^{-1}\)。
n = my_data.shape[0]
nu_prior = PRIOR_DF
v_prior = PRIOR_SCALE
nu_posterior = nu_prior + n
v_posterior = np.linalg.inv(np.linalg.inv(v_prior) + my_data.T.dot(my_data))
posterior_mean = nu_posterior * v_posterior
v_post_diag = np.expand_dims(np.diag(v_posterior), axis=1)
posterior_sd = np.sqrt(nu_posterior *
(v_posterior ** 2.0 + v_post_diag.dot(v_post_diag.T)))
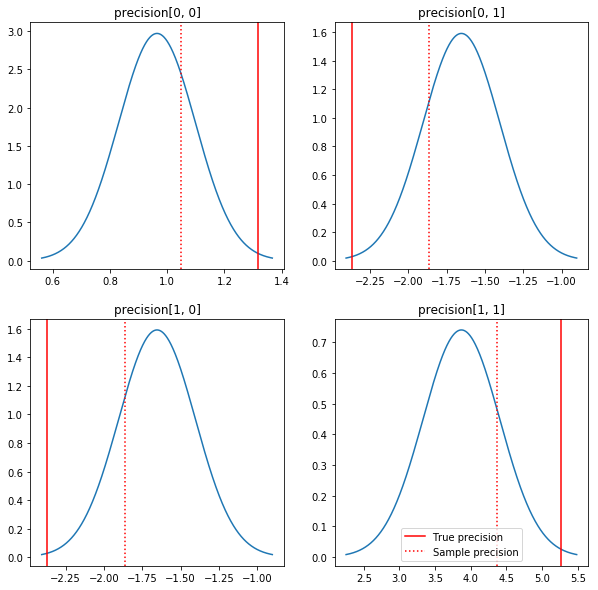
后验和真实值的快速绘制。请注意,后验接近样本后验,但略微收缩到单位矩阵。还要注意,真实值与后验的模式相距甚远 - 推测这是因为先验与我们的数据不太匹配。在实际问题中,我们可能会使用像缩放的逆 Wishart 先验来更好地估计协方差(例如,参见 Andrew Gelman 关于该主题的 评论),但随后我们将没有一个很好的解析后验。
sample_precision = np.linalg.inv(np.cov(my_data, rowvar=False, bias=False))
fig, axes = plt.subplots(2, 2)
fig.set_size_inches(10, 10)
for i in range(2):
for j in range(2):
ax = axes[i, j]
loc = posterior_mean[i, j]
scale = posterior_sd[i, j]
xmin = loc - 3.0 * scale
xmax = loc + 3.0 * scale
x = np.linspace(xmin, xmax, 1000)
y = scipy.stats.norm.pdf(x, loc=loc, scale=scale)
ax.plot(x, y)
ax.axvline(true_precision[i, j], color='red', label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':', label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.legend()
plt.show()
步骤 3:在 TensorFlow 中实现似然函数
剧透:我们的第一次尝试不会成功;我们将在下面讨论原因。
提示:在开发似然函数时使用 TensorFlow 渴望模式。渴望模式使 TF 的行为更像 NumPy - 一切立即执行,因此您可以交互式地进行调试,而无需使用 Session.run()。请参阅 此处 的说明。
初步:分布类
TFP 有一组分布类,我们将使用这些类来生成我们的对数概率。需要注意的一点是,这些类使用样本张量而不是单个样本 - 这允许矢量化和相关的加速。
分布可以通过两种不同的方式使用样本张量。用一个包含单个标量参数的分布的具体示例来说明这两种方式最简单。我将使用 泊松 分布,它具有 rate 参数。
- 如果我们使用
rate参数的单个值创建一个泊松,则调用其sample()方法将返回一个值。此值称为事件,在本例中,所有事件都是标量。 - 如果我们使用
rate参数的张量值创建一个泊松,则调用其sample()方法现在将返回多个值,每个rate张量中的值一个。该对象充当独立泊松的集合,每个泊松都有自己的速率,并且sample()调用返回的每个值都对应于这些泊松之一。此独立的但不是同分布的事件集合称为批次。 sample()方法接受一个sample_shape参数,该参数默认为空元组。传递sample_shape的非空值会导致样本返回多个批次。此批次集合称为样本。
分布的 log_prob() 方法以与 sample() 生成方式类似的方式使用数据。 log_prob() 返回样本的概率,即多个独立批次的事件的概率。
- 如果我们有一个使用标量
rate创建的泊松对象,则每个批次都是一个标量,如果我们传入一个样本张量,我们将得到一个相同大小的对数概率张量。 - 如果我们有一个使用形状为
T的rate值张量创建的泊松对象,则每个批次都是一个形状为T的张量。如果我们传入一个形状为 D, T 的样本张量,我们将得到一个形状为 D, T 的对数概率张量。
下面是一些说明这些情况的示例。有关事件、批次和形状的更详细教程,请参阅 此笔记本。
# case 1: get log probabilities for a vector of iid draws from a single
# normal distribution
norm1 = tfd.Normal(loc=0., scale=1.)
probs1 = norm1.log_prob(tf.constant([1., 0.5, 0.]))
# case 2: get log probabilities for a vector of independent draws from
# multiple normal distributions with different parameters. Note the vector
# values for loc and scale in the Normal constructor.
norm2 = tfd.Normal(loc=[0., 2., 4.], scale=[1., 1., 1.])
probs2 = norm2.log_prob(tf.constant([1., 0.5, 0.]))
print('iid draws from a single normal:', probs1.numpy())
print('draws from a batch of normals:', probs2.numpy())
iid draws from a single normal: [-1.4189385 -1.0439385 -0.9189385] draws from a batch of normals: [-1.4189385 -2.0439386 -8.918939 ]
数据对数似然
首先,我们将实现数据对数似然函数。
VALIDATE_ARGS = True
ALLOW_NAN_STATS = False
与 NumPy 案例的一个关键区别在于,我们的 TensorFlow 似然函数需要处理精度矩阵向量,而不仅仅是单个矩阵。当我们从多个链中采样时,将使用参数向量。
我们将创建一个与精度矩阵批次(即每个链一个矩阵)一起使用的分布对象。
在计算数据的对数概率时,我们需要以与参数相同的方式复制数据,以便每个批次变量都有一个副本。我们复制数据的形状需要如下所示
[样本形状,批次形状,事件形状]
在我们的例子中,事件形状为 2(因为我们使用的是二维高斯)。样本形状为 100,因为我们有 100 个样本。批次形状将只是我们正在使用的精度矩阵的数量。每次调用似然函数时复制数据效率低下,因此我们将提前复制数据并传入复制的版本。
请注意,这是一个低效的实现:MultivariateNormalFullCovariance 相对于我们将在优化部分最后讨论的一些替代方案来说成本很高。
def log_lik_data(precisions, replicated_data):
n = tf.shape(precisions)[0] # number of precision matrices
# We're estimating a precision matrix; we have to invert to get log
# probabilities. Cholesky inversion should be relatively efficient,
# but as we'll see later, it's even better if we can avoid doing the Cholesky
# decomposition altogether.
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# For our test, we'll use a tensor of 2 precision matrices.
# We'll need to replicate our data for the likelihood function.
# Remember, TFP wants the data to be structured so that the sample dimensions
# are first (100 here), then the batch dimensions (2 here because we have 2
# precision matrices), then the event dimensions (2 because we have 2-D
# Gaussian data). We'll need to add a middle dimension for the batch using
# expand_dims, and then we'll need to create 2 replicates in this new dimension
# using tile.
n = 2
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
print(replicated_data.shape)
(100, 2, 2)
提示:我发现非常有帮助的一件事是编写 TensorFlow 函数的小型健全性检查。在 TF 中弄乱矢量化非常容易,因此使用更简单的 NumPy 函数是一个很好的方法来验证 TF 输出。将这些视为小型单元测试。
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_data(precisions, replicated_data=replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
先验对数似然
先验更容易,因为我们不必担心数据复制。
@tf.function(autograph=False)
def log_lik_prior(precisions):
rv_precision = tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions)
# check against the numpy implementation
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
n = precisions.shape[0]
lik_tf = log_lik_prior(precisions).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]))
print('tensorflow:', lik_tf[i])
0 numpy: -2.2351873809649625 tensorflow: -2.2351875 1 numpy: -9.103606346649766 tensorflow: -9.103608
构建联合对数似然函数
上面的数据对数似然函数依赖于我们的观测值,但采样器不会拥有这些观测值。我们可以通过使用 [闭包](https://en.wikipedia.org/wiki/Closure_(computer_programming) 来消除对全局变量的依赖。闭包涉及一个外部函数,该函数构建一个包含内部函数所需变量的环境。
def get_log_lik(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik(precision):
return log_lik_data(precision, replicated_data) + log_lik_prior(precision)
return _log_lik
步骤 4:采样
好的,是时候采样了!为了简单起见,我们将只使用 1 条链,并将使用单位矩阵作为起点。我们将在稍后更仔细地进行操作。
同样,这不会成功 - 我们将得到一个异常。
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.expand_dims(tf.eye(2), axis=0)
# Use expand_dims because we want to pass in a tensor of starting values
log_lik_fn = get_log_lik(my_data, n_chains=1)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
return states
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
Cholesky decomposition was not successful. The input might not be valid.
[[{ {node mcmc_sample_chain/trace_scan/while/body/_79/smart_for_loop/while/body/_371/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_537/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/StatefulPartitionedCall/Cholesky} }]] [Op:__inference_sample_2849]
Function call stack:
sample
...
Function call stack:
sample
识别问题
InvalidArgumentError (see above for traceback): Cholesky decomposition was not successful. The input might not be valid. 这不是很有帮助。让我们看看是否可以找到更多有关发生情况的信息。
- 我们将打印出每个步骤的参数,以便我们可以看到导致失败的值。
- 我们将添加一些断言来防止特定问题。
断言很棘手,因为它们是 TensorFlow 操作,我们必须注意它们被执行并且不会被从图中优化掉。如果你不熟悉 TF 断言,值得阅读 这个概述。你可以使用 tf.control_dependencies(参见下面代码中的注释)显式强制断言执行。
TensorFlow 的原生 Print 函数与断言具有相同的行为 - 它是一个操作,你需要注意确保它执行。 Print 在我们使用笔记本时会导致额外的麻烦:它的输出被发送到 stderr,而 stderr 不会在单元格中显示。我们将在这里使用一个技巧:而不是使用 tf.Print,我们将通过 tf.pyfunc 创建我们自己的 TensorFlow 打印操作。与断言一样,我们必须确保我们的方法执行。
def get_log_lik_verbose(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
def _log_lik(precisions):
# An internal method we'll make into a TensorFlow operation via tf.py_func
def _print_precisions(precisions):
print('precisions:\n', precisions)
return False # operations must return something!
# Turn our method into a TensorFlow operation
print_op = tf.compat.v1.py_func(_print_precisions, [precisions], tf.bool)
# Assertions are also operations, and some care needs to be taken to ensure
# that they're executed
assert_op = tf.assert_equal(
precisions, tf.linalg.matrix_transpose(precisions),
message='not symmetrical', summarize=4, name='symmetry_check')
# The control_dependencies statement forces its arguments to be executed
# before subsequent operations
with tf.control_dependencies([print_op, assert_op]):
return (log_lik_data(precisions, replicated_data) +
log_lik_prior(precisions))
return _log_lik
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
init_precision = tf.eye(2)[tf.newaxis, ...]
log_lik_fn = get_log_lik_verbose(my_data)
# we'll just do a few steps here
num_results = 10
num_burnin_steps = 10
states = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
init_precision,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=None,
seed=123)
try:
states = sample()
except Exception as e:
# shorten the giant stack trace
lines = str(e).split('\n')
print('\n'.join(lines[:5]+['...']+lines[-3:]))
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[1. 0.]
[0. 1.]]]
precisions:
[[[ 0.24315196 -0.2761638 ]
[-0.33882257 0.8622 ]]]
assertion failed: [not symmetrical] [Condition x == y did not hold element-wise:] [x (leapfrog_integrate_one_step/add:0) = ] [[[0.243151963 -0.276163787][-0.338822573 0.8622]]] [y (leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/matrix_transpose/transpose:0) = ] [[[0.243151963 -0.338822573][-0.276163787 0.8622]]]
[[{ {node mcmc_sample_chain/trace_scan/while/body/_96/smart_for_loop/while/body/_381/mh_one_step/hmc_kernel_one_step/leapfrog_integrate/while/body/_503/leapfrog_integrate_one_step/maybe_call_fn_and_grads/value_and_gradients/symmetry_check_1/Assert/AssertGuard/else/_577/Assert} }]] [Op:__inference_sample_4837]
Function call stack:
sample
...
Function call stack:
sample
为什么这会失败
采样器尝试的第一个新参数值是一个非对称矩阵。这会导致 Cholesky 分解失败,因为它只针对对称(和正定)矩阵定义。
这里的问题是,我们感兴趣的参数是一个精度矩阵,精度矩阵必须是实数、对称且正定。采样器对这个约束一无所知(除了可能通过梯度),因此采样器完全有可能提出一个无效的值,从而导致异常,特别是如果步长很大。
使用哈密顿蒙特卡罗采样器,我们可能能够通过使用非常小的步长来解决这个问题,因为梯度应该将参数保持在无效区域之外,但小的步长意味着收敛速度慢。使用不知道任何梯度信息的 Metropolis-Hastings 采样器,我们注定要失败。
版本 2:重新参数化为无约束参数
上面问题有一个简单的解决方案:我们可以重新参数化我们的模型,使得新参数不再具有这些约束。TFP 提供了一套有用的工具 - 双射器 - 用于执行此操作。
使用双射器重新参数化
我们的精度矩阵必须是实数且对称;我们想要一个没有这些约束的替代参数化。一个起点是精度矩阵的 Cholesky 分解。Cholesky 因子仍然受到约束 - 它们是下三角的,并且它们的对角元素必须为正。但是,如果我们取 Cholesky 因子的对角线的对数,对数不再受限于为正,然后如果我们将下三角部分展平为一维向量,我们就不再有下三角约束。在我们这个案例中,结果将是一个长度为 3 的向量,没有任何约束。
(Stan 手册 有一章关于使用变换来消除参数上的各种约束。)
这种重新参数化对我们的数据对数似然函数影响很小 - 我们只需要反转我们的变换以获得精度矩阵 - 但对先验的影响更复杂。我们已经指定了给定精度矩阵的概率由 Wishart 分布给出;我们变换后的矩阵的概率是多少?
回想一下,如果我们将单调函数 \(g\) 应用于一维随机变量 \(X\),\(Y = g(X)\),则 \(Y\) 的密度由下式给出
\[ f_Y(y) = | \frac{d}{dy}(g^{-1}(y)) | f_X(g^{-1}(y)) \]
\(g^{-1}\) 项的导数解释了 \(g\) 如何改变局部体积。对于更高维度的随机变量,校正因子是 \(g^{-1}\) 的雅可比行列式的绝对值(参见 这里)。
我们必须将逆变换的雅可比行列式添加到我们的对数先验似然函数中。幸运的是,TFP 的 Bijector 类可以为我们处理这个问题。
Bijector 类用于表示可逆的、平滑的函数,用于在概率密度函数中改变变量。所有双射器都有一个 forward() 方法执行变换,一个 inverse() 方法反转它,以及 forward_log_det_jacobian() 和 inverse_log_det_jacobian() 方法,这些方法提供了我们在重新参数化 pdf 时需要的雅可比校正。
TFP 提供了一组有用的双射器,我们可以通过 Chain 运算符的组合来组合它们,以形成相当复杂的变换。在我们的案例中,我们将组合以下 3 个双射器(链中的操作是从右到左执行的)
- 我们变换的第一步是对精度矩阵执行 Cholesky 分解。没有一个 Bijector 类可以做到这一点;但是,
CholeskyOuterProduct双射器取 2 个 Cholesky 因子的乘积。我们可以使用Invert运算符的反向操作。 - 下一步是取 Cholesky 因子的对角元素的对数。我们通过
TransformDiagonal双射器和Exp双射器的逆来实现这一点。 - 最后,我们使用
FillTriangular双射器的逆将矩阵的下三角部分展平为向量。
# Our transform has 3 stages that we chain together via composition:
precision_to_unconstrained = tfb.Chain([
# step 3: flatten the lower triangular portion of the matrix
tfb.Invert(tfb.FillTriangular(validate_args=VALIDATE_ARGS)),
# step 2: take the log of the diagonals
tfb.TransformDiagonal(tfb.Invert(tfb.Exp(validate_args=VALIDATE_ARGS))),
# step 1: decompose the precision matrix into its Cholesky factors
tfb.Invert(tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS)),
])
# sanity checks
m = tf.constant([[1., 2.], [2., 8.]])
m_fwd = precision_to_unconstrained.forward(m)
m_inv = precision_to_unconstrained.inverse(m_fwd)
# bijectors handle tensors of values, too!
m2 = tf.stack([m, tf.eye(2)])
m2_fwd = precision_to_unconstrained.forward(m2)
m2_inv = precision_to_unconstrained.inverse(m2_fwd)
print('single input:')
print('m:\n', m.numpy())
print('precision_to_unconstrained(m):\n', m_fwd.numpy())
print('inverse(precision_to_unconstrained(m)):\n', m_inv.numpy())
print()
print('tensor of inputs:')
print('m2:\n', m2.numpy())
print('precision_to_unconstrained(m2):\n', m2_fwd.numpy())
print('inverse(precision_to_unconstrained(m2)):\n', m2_inv.numpy())
single input: m: [[1. 2.] [2. 8.]] precision_to_unconstrained(m): [0.6931472 2. 0. ] inverse(precision_to_unconstrained(m)): [[1. 2.] [2. 8.]] tensor of inputs: m2: [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]] precision_to_unconstrained(m2): [[0.6931472 2. 0. ] [0. 0. 0. ]] inverse(precision_to_unconstrained(m2)): [[[1. 2.] [2. 8.]] [[1. 0.] [0. 1.]]]
TransformedDistribution 类自动执行将双射器应用于分布并对 log_prob() 进行必要的雅可比校正的过程。我们的新先验变为
def log_lik_prior_transformed(transformed_precisions):
rv_precision = tfd.TransformedDistribution(
tfd.WishartTriL(
df=PRIOR_DF,
scale_tril=tf.linalg.cholesky(PRIOR_SCALE),
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS),
bijector=precision_to_unconstrained,
validate_args=VALIDATE_ARGS)
return rv_precision.log_prob(transformed_precisions)
# Check against the numpy implementation. Note that when comparing, we need
# to add in the Jacobian correction.
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_prior_transformed(transformed_precisions).numpy()
corrections = precision_to_unconstrained.inverse_log_det_jacobian(
transformed_precisions, event_ndims=1).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow: -0.84889317 1 numpy: -7.305657151741624 tensorflow: -7.305659
我们只需要反转变换以获得我们的数据对数似然
precision = precision_to_unconstrained.inverse(transformed_precision)
由于我们实际上想要精度矩阵的 Cholesky 分解,因此在这里进行部分逆运算会更有效。但是,我们将优化留到以后,并将部分逆运算留给读者作为练习。
def log_lik_data_transformed(transformed_precisions, replicated_data):
# We recover the precision matrix by inverting our bijector. This is
# inefficient since we really want the Cholesky decomposition of the
# precision matrix, and the bijector has that in hand during the inversion,
# but we'll worry about efficiency later.
n = tf.shape(transformed_precisions)[0]
precisions = precision_to_unconstrained.inverse(transformed_precisions)
precisions_cholesky = tf.linalg.cholesky(precisions)
covariances = tf.linalg.cholesky_solve(
precisions_cholesky, tf.linalg.eye(2, batch_shape=[n]))
rv_data = tfd.MultivariateNormalFullCovariance(
loc=tf.zeros([n, 2]),
covariance_matrix=covariances,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# sanity check
precisions = np.stack([np.eye(2, dtype=np.float32), true_precision])
transformed_precisions = precision_to_unconstrained.forward(precisions)
lik_tf = log_lik_data_transformed(
transformed_precisions, replicated_data).numpy()
for i in range(precisions.shape[0]):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.8182
我们再次将我们的新函数包装在一个闭包中。
def get_log_lik_transformed(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_transformed(transformed_precisions):
return (log_lik_data_transformed(transformed_precisions, replicated_data) +
log_lik_prior_transformed(transformed_precisions))
return _log_lik_transformed
# make sure everything runs
log_lik_fn = get_log_lik_transformed(my_data)
m = tf.eye(2)[tf.newaxis, ...]
lik = log_lik_fn(precision_to_unconstrained.forward(m)).numpy()
print(lik)
[-431.5611]
采样
现在我们不必担心我们的采样器由于无效的参数值而爆炸,让我们生成一些真实的样本。
采样器使用我们参数的无约束版本,因此我们需要将我们的初始值转换为其无约束版本。我们生成的样本也将全部以其无约束形式存在,因此我们需要将它们转换回来。双射器是向量化的,因此这样做很容易。
# We'll choose a proper random initial value this time
np.random.seed(123)
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_value = initial_value_cholesky.dot(
initial_value_cholesky.T)[np.newaxis, ...]
# The sampler works with unconstrained values, so we'll transform our initial
# value
initial_value_transformed = precision_to_unconstrained.forward(
initial_value).numpy()
# Sample!
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data, n_chains=1)
num_results = 1000
num_burnin_steps = 1000
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
initial_value_transformed,
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.1,
num_leapfrog_steps=3),
trace_fn=lambda _, pkr: pkr.is_accepted,
seed=123)
# transform samples back to their constrained form
precision_samples = [precision_to_unconstrained.inverse(s) for s in states]
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
让我们将采样器输出的平均值与解析后验平均值进行比较!
print('True posterior mean:\n', posterior_mean)
print('Sample mean:\n', np.mean(np.reshape(precision_samples, [-1, 2, 2]), axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Sample mean: [[ 1.4315274 -0.25587553] [-0.25587553 0.5740424 ]]
我们错了!让我们找出原因。首先让我们看看我们的样本。
np.reshape(precision_samples, [-1, 2, 2])
array([[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
...,
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]],
[[ 1.4315385, -0.2558777],
[-0.2558777, 0.5740494]]], dtype=float32)
糟糕 - 它们似乎都具有相同的值。让我们找出原因。
kernel_results_ 变量是一个命名元组,它提供了每个状态下采样器的信息。 is_accepted 字段是这里的关键。
# Look at the acceptance for the last 100 samples
print(np.squeeze(is_accepted)[-100:])
print('Fraction of samples accepted:', np.mean(np.squeeze(is_accepted)))
[False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False False] Fraction of samples accepted: 0.0
我们所有的样本都被拒绝了!可能我们的步长太大。我纯粹是随意选择 stepsize=0.1。
版本 3:使用自适应步长进行采样
由于使用我随意选择的步长进行采样失败了,我们有一些议程项目
- 实现自适应步长,以及
- 执行一些收敛检查。
在 tensorflow_probability/python/mcmc/hmc.py 中有一些很好的示例代码用于实现自适应步长。我在下面对其进行了改编。
请注意,每个步骤都有一个单独的 sess.run() 语句。这对于调试非常有用,因为它允许我们在需要时轻松添加一些每步诊断。例如,我们可以显示增量进度,计时每个步骤等。
提示:一种明显常见的搞砸采样的方法是让你的图在循环中增长。(在运行会话之前完成图的原因是为了防止出现此类问题。)如果你没有使用 finalize(),那么如果你的代码速度变慢,一个有用的调试检查是通过 len(mygraph.get_operations()) 打印出每个步骤的图大小 - 如果长度增加,你可能在做一些不好的事情。
我们将在这里运行 3 个独立的链。在链之间进行一些比较将有助于我们检查收敛。
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values = []
for i in range(N_CHAINS):
initial_value_cholesky = np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32)
initial_values.append(initial_value_cholesky.dot(initial_value_cholesky.T))
initial_values = np.stack(initial_values)
initial_values_transformed = precision_to_unconstrained.forward(
initial_values).numpy()
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_transformed(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=hmc,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states, is_accepted = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values_transformed,
kernel=adapted_kernel,
trace_fn=lambda _, pkr: pkr.inner_results.is_accepted,
parallel_iterations=1)
# transform samples back to their constrained form
precision_samples = precision_to_unconstrained.inverse(states)
return states, precision_samples, is_accepted
states, precision_samples, is_accepted = sample()
快速检查:我们采样过程中的接受率接近我们目标的 0.651。
print(np.mean(is_accepted))
0.6190666666666667
更棒的是,我们的样本均值和标准差接近我们从解析解中得到的预期值。
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96426415 -1.6519215 ] [-1.6519215 3.8614824 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13622096 0.25235635] [0.25235635 0.5394968 ]]
检查收敛
通常我们没有解析解来进行检查,因此我们需要确保采样器已收敛。一个标准检查是 Gelman-Rubin \(\hat{R}\) 统计量,它需要多个采样链。 \(\hat{R}\) 测量链之间方差(均值的方差)超过如果链具有相同分布所期望的程度。 \(\hat{R}\) 的值接近 1 用于指示近似收敛。有关详细信息,请参见 源代码。
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0038308 1.0005717] [1.0005717 1.0006068]]
模型批判
如果我们没有解析解,那么现在就是进行一些真正的模型批判的时候了。
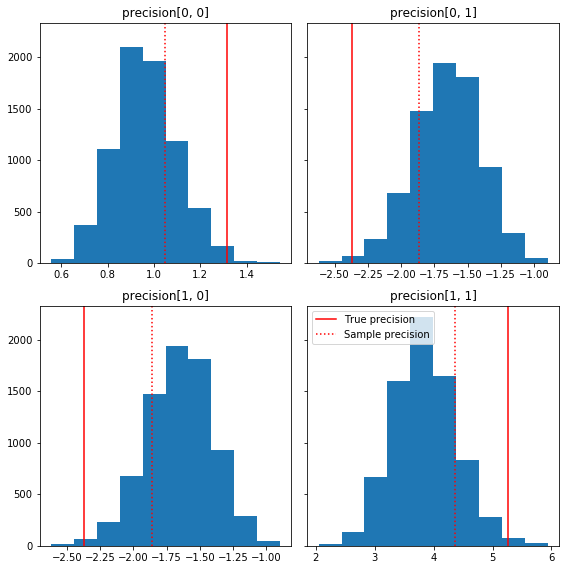
以下是一些关于样本分量相对于我们的真实值(红色)的快速直方图。请注意,样本已从样本精度矩阵值缩小到身份矩阵先验。
fig, axes = plt.subplots(2, 2, sharey=True)
fig.set_size_inches(8, 8)
for i in range(2):
for j in range(2):
ax = axes[i, j]
ax.hist(precision_samples_reshaped[:, i, j])
ax.axvline(true_precision[i, j], color='red',
label='True precision')
ax.axvline(sample_precision[i, j], color='red', linestyle=':',
label='Sample precision')
ax.set_title('precision[%d, %d]' % (i, j))
plt.tight_layout()
plt.legend()
plt.show()
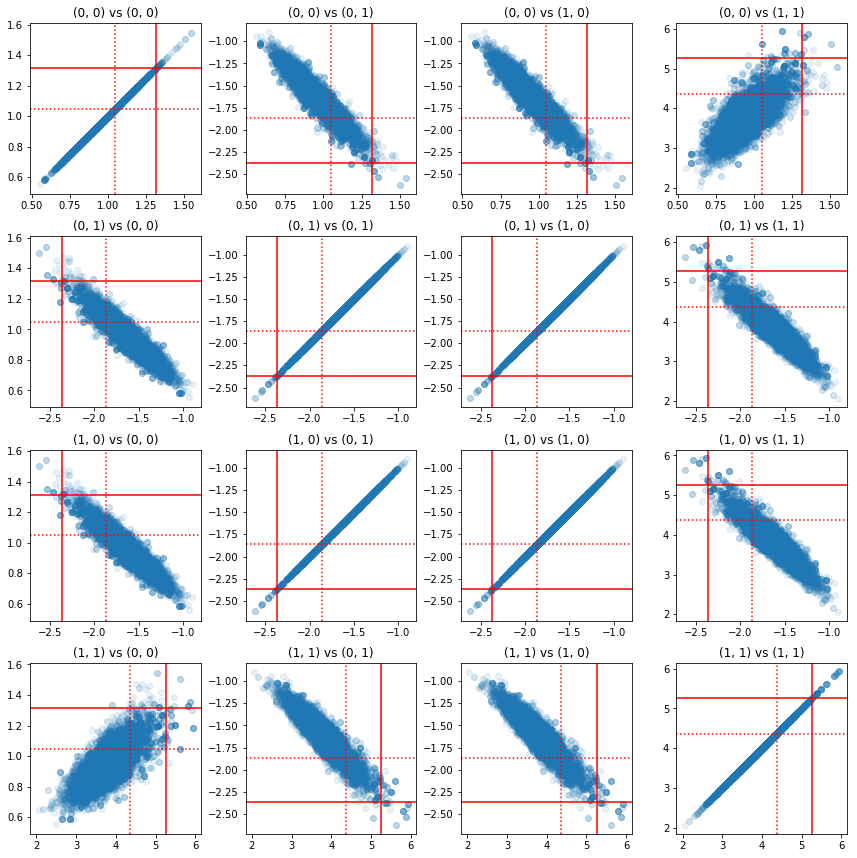
一些精度分量对的散点图表明,由于后验的相关结构,真实后验值不像上面从边缘分布中看到的那样不可能。
fig, axes = plt.subplots(4, 4)
fig.set_size_inches(12, 12)
for i1 in range(2):
for j1 in range(2):
index1 = 2 * i1 + j1
for i2 in range(2):
for j2 in range(2):
index2 = 2 * i2 + j2
ax = axes[index1, index2]
ax.scatter(precision_samples_reshaped[:, i1, j1],
precision_samples_reshaped[:, i2, j2], alpha=0.1)
ax.axvline(true_precision[i1, j1], color='red')
ax.axhline(true_precision[i2, j2], color='red')
ax.axvline(sample_precision[i1, j1], color='red', linestyle=':')
ax.axhline(sample_precision[i2, j2], color='red', linestyle=':')
ax.set_title('(%d, %d) vs (%d, %d)' % (i1, j1, i2, j2))
plt.tight_layout()
plt.show()
版本 4:对约束参数进行更简单的采样
双射器使对精度矩阵进行采样变得简单,但需要大量手动转换到无约束表示和从无约束表示转换回来。有一个更简单的方法!
TransformedTransitionKernel
TransformedTransitionKernel 简化了这个过程。它包装你的采样器并处理所有转换。它接受一个双射器列表作为参数,这些双射器将无约束参数值映射到约束参数值。因此,这里我们需要上面使用的 precision_to_unconstrained 双射器的逆。我们可以直接使用 tfb.Invert(precision_to_unconstrained),但这将涉及对逆运算进行逆运算(TensorFlow 不够聪明,无法将 tf.Invert(tf.Invert()) 简化为 tf.Identity()),因此我们将编写一个新的双射器。
约束双射器
# The bijector we need for the TransformedTransitionKernel is the inverse of
# the one we used above
unconstrained_to_precision = tfb.Chain([
# step 3: take the product of Cholesky factors
tfb.CholeskyOuterProduct(validate_args=VALIDATE_ARGS),
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: map a vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# quick sanity check
m = [[1., 2.], [2., 8.]]
m_inv = unconstrained_to_precision.inverse(m).numpy()
m_fwd = unconstrained_to_precision.forward(m_inv).numpy()
print('m:\n', m)
print('unconstrained_to_precision.inverse(m):\n', m_inv)
print('forward(unconstrained_to_precision.inverse(m)):\n', m_fwd)
m: [[1.0, 2.0], [2.0, 8.0]] unconstrained_to_precision.inverse(m): [0.6931472 2. 0. ] forward(unconstrained_to_precision.inverse(m)): [[1. 2.] [2. 8.]]
使用 TransformedTransitionKernel 进行采样
使用 TransformedTransitionKernel,我们不再需要手动转换我们的参数。我们的初始值和我们的样本都是精度矩阵;我们只需要将我们的无约束双射器传递给内核,它会处理所有转换。
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
return states
precision_samples = sample()
检查收敛
\(\hat{R}\) 收敛检查看起来不错!
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013582 1.0019467] [1.0019467 1.0011805]]
与解析后验进行比较
让我们再次与解析后验进行比较。
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, [-1, 2, 2])
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.96687526 -1.6552585 ] [-1.6552585 3.867676 ]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329624 0.24913791] [0.24913791 0.53983927]]
优化
现在我们已经让所有东西都能正常运行了,让我们来做一个更优化的版本。速度对于这个例子来说并不重要,但是一旦矩阵变得更大,一些优化就会产生很大的影响。
我们可以做出的一个重大速度改进是根据 Cholesky 分解进行重新参数化。原因是我们的数据似然函数需要协方差矩阵和精度矩阵。矩阵求逆很昂贵(对于 \(n \times n\) 矩阵,\(O(n^3)\)),如果我们根据协方差矩阵或精度矩阵进行参数化,我们需要进行求逆才能得到另一个矩阵。
提醒一下,一个实数、正定、对称矩阵 \(M\) 可以分解成 \(M = L L^T\) 形式的乘积,其中矩阵 \(L\) 是下三角矩阵,并且具有正的对角线。给定 \(M\) 的 Cholesky 分解,我们可以更有效地获得 \(M\)(下三角矩阵和上三角矩阵的乘积)和 \(M^{-1}\)(通过回代)。Cholesky 分解本身计算起来并不便宜,但是如果我们根据 Cholesky 因子进行参数化,我们只需要计算初始参数值的 Cholesky 分解。
使用协方差矩阵的 Cholesky 分解
TFP 有一个多元正态分布版本,MultivariateNormalTriL,它根据协方差矩阵的 Cholesky 因子进行参数化。因此,如果我们根据协方差矩阵的 Cholesky 因子进行参数化,我们可以有效地计算数据对数似然。挑战在于以类似的效率计算先验对数似然。
如果我们有一个适用于样本的 Cholesky 因子的逆 Wishart 分布版本,我们就可以搞定了。可惜,我们没有。(不过,团队欢迎代码提交!)作为替代方案,我们可以使用一个适用于样本的 Cholesky 因子的 Wishart 分布版本,以及一系列双射函数。
目前,我们缺少一些常用的双射函数来真正提高效率,但我希望将这个过程作为一个练习,并说明 TFP 双射函数的强大功能。
一个在 Cholesky 因子上操作的 Wishart 分布
该 Wishart 分布有一个有用的标志,input_output_cholesky,它指定输入和输出矩阵应该是 Cholesky 因子。使用 Cholesky 因子比使用完整矩阵更有效,在数值上也更有优势,这就是为什么这是可取的。关于该标志语义的一个重要点:它只表示输入和输出到分布的表示应该改变 - 它并不表示分布的完全重新参数化,这将涉及对 log_prob() 函数的雅可比修正。我们实际上想要进行这种完全重新参数化,因此我们将构建我们自己的分布。
# An optimized Wishart distribution that has been transformed to operate on
# Cholesky factors instead of full matrices. Note that we gain a modest
# additional speedup by specifying the Cholesky factor of the scale matrix
# (i.e. by passing in the scale_tril parameter instead of scale).
class CholeskyWishart(tfd.TransformedDistribution):
"""Wishart distribution reparameterized to use Cholesky factors."""
def __init__(self,
df,
scale_tril,
validate_args=False,
allow_nan_stats=True,
name='CholeskyWishart'):
# Wishart has a bunch of methods that we want to support but not
# implement. We'll subclass TransformedDistribution here to take care of
# those. We'll override the few for which speed is critical and implement
# them with a separate Wishart for which input_output_cholesky=True
super(CholeskyWishart, self).__init__(
distribution=tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=False,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()),
validate_args=validate_args,
name=name
)
# Here's the Cholesky distribution we'll use for log_prob() and sample()
self.cholesky = tfd.WishartTriL(
df=df,
scale_tril=scale_tril,
input_output_cholesky=True,
validate_args=validate_args,
allow_nan_stats=allow_nan_stats)
def _log_prob(self, x):
return (self.cholesky.log_prob(x) +
self.bijector.inverse_log_det_jacobian(x, event_ndims=2))
def _sample_n(self, n, seed=None):
return self.cholesky._sample_n(n, seed)
# some checks
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
@tf.function(autograph=False)
def compute_log_prob(m):
w_transformed = tfd.TransformedDistribution(
tfd.WishartTriL(df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY),
bijector=tfb.Invert(tfb.CholeskyOuterProduct()))
w_optimized = CholeskyWishart(
df=PRIOR_DF, scale_tril=PRIOR_SCALE_CHOLESKY)
log_prob_transformed = w_transformed.log_prob(m)
log_prob_optimized = w_optimized.log_prob(m)
return log_prob_transformed, log_prob_optimized
for matrix in [np.eye(2, dtype=np.float32),
np.array([[1., 0.], [2., 8.]], dtype=np.float32)]:
log_prob_transformed, log_prob_optimized = [
t.numpy() for t in compute_log_prob(matrix)]
print('Transformed Wishart:', log_prob_transformed)
print('Optimized Wishart', log_prob_optimized)
Transformed Wishart: -0.84889317 Optimized Wishart -0.84889317 Transformed Wishart: -99.269455 Optimized Wishart -99.269455
构建一个逆 Wishart 分布
我们有协方差矩阵 \(C\) 分解成 \(C = L L^T\),其中 \(L\) 是下三角矩阵,并且具有正的对角线。我们想知道 \(L\) 的概率,前提是 \(C \sim W^{-1}(\nu, V)\),其中 \(W^{-1}\) 是逆 Wishart 分布。
逆 Wishart 分布具有以下性质:如果 \(C \sim W^{-1}(\nu, V)\),则精度矩阵 \(C^{-1} \sim W(\nu, V^{-1})\)。因此,我们可以通过一个 TransformedDistribution 来获得 \(L\) 的概率,该分布将 Wishart 分布和一个双射函数作为参数,该双射函数将精度矩阵的 Cholesky 因子映射到其逆的 Cholesky 因子。
从 \(C^{-1}\) 的 Cholesky 因子到 \(L\) 的一个简单(但效率不高)的方法是通过回代求解来求逆 Cholesky 因子,然后根据这些求逆的因子形成协方差矩阵,然后进行 Cholesky 分解。
令 \(C^{-1} = M M^T\) 的 Cholesky 分解。\(M\) 是下三角矩阵,因此我们可以使用 MatrixInverseTriL 双射函数对其进行求逆。
从 \(M^{-1}\) 形成 \(C\) 有点棘手:\(C = (M M^T)^{-1} = M^{-T}M^{-1} = M^{-T} (M^{-T})^T\)。\(M\) 是下三角矩阵,因此 \(M^{-1}\) 也是下三角矩阵,而 \(M^{-T}\) 是上三角矩阵。该 CholeskyOuterProduct() 双射函数仅适用于下三角矩阵,因此我们无法使用它从 \(M^{-T}\) 形成 \(C\)。我们的解决方法是使用一系列双射函数来置换矩阵的行和列。
幸运的是,这种逻辑封装在 CholeskyToInvCholesky 双射函数中!
组合所有部分
# verify that the bijector works
m = np.array([[1., 0.], [2., 8.]], dtype=np.float32)
c_inv = m.dot(m.T)
c = np.linalg.inv(c_inv)
c_chol = np.linalg.cholesky(c)
wishart_cholesky_to_iw_cholesky = tfb.CholeskyToInvCholesky()
w_fwd = wishart_cholesky_to_iw_cholesky.forward(m).numpy()
print('numpy =\n', c_chol)
print('bijector =\n', w_fwd)
numpy = [[ 1.0307764 0. ] [-0.03031695 0.12126781]] bijector = [[ 1.0307764 0. ] [-0.03031695 0.12126781]]
我们的最终分布
我们操作 Cholesky 因子的逆 Wishart 如下所示
inverse_wishart_cholesky = tfd.TransformedDistribution(
distribution=CholeskyWishart(
df=PRIOR_DF,
scale_tril=np.linalg.cholesky(np.linalg.inv(PRIOR_SCALE))),
bijector=tfb.CholeskyToInvCholesky())
我们已经得到了我们的逆 Wishart,但它有点慢,因为我们必须在双射函数中进行 Cholesky 分解。让我们回到精度矩阵参数化,看看我们可以在那里做些什么来进行优化。
最终(!)版本:使用精度矩阵的 Cholesky 分解
另一种方法是使用精度矩阵的 Cholesky 因子。在这里,先验似然函数很容易计算,但数据对数似然函数需要更多工作,因为 TFP 没有一个根据精度进行参数化的多元正态分布版本。
优化的先验对数似然
我们使用上面构建的 CholeskyWishart 分布来构建先验。
# Our new prior.
PRIOR_SCALE_CHOLESKY = np.linalg.cholesky(PRIOR_SCALE)
def log_lik_prior_cholesky(precisions_cholesky):
rv_precision = CholeskyWishart(
df=PRIOR_DF,
scale_tril=PRIOR_SCALE_CHOLESKY,
validate_args=VALIDATE_ARGS,
allow_nan_stats=ALLOW_NAN_STATS)
return rv_precision.log_prob(precisions_cholesky)
# Check against the slower TF implementation and the NumPy implementation.
# Note that when comparing to NumPy, we need to add in the Jacobian correction.
precisions = [np.eye(2, dtype=np.float32),
true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
lik_tf = log_lik_prior_cholesky(precisions_cholesky).numpy()
lik_tf_slow = tfd.TransformedDistribution(
distribution=tfd.WishartTriL(
df=PRIOR_DF, scale_tril=tf.linalg.cholesky(PRIOR_SCALE)),
bijector=tfb.Invert(tfb.CholeskyOuterProduct())).log_prob(
precisions_cholesky).numpy()
corrections = tfb.Invert(tfb.CholeskyOuterProduct()).inverse_log_det_jacobian(
precisions_cholesky, event_ndims=2).numpy()
n = precisions.shape[0]
for i in range(n):
print(i)
print('numpy:', log_lik_prior_numpy(precisions[i]) + corrections[i])
print('tensorflow slow:', lik_tf_slow[i])
print('tensorflow fast:', lik_tf[i])
0 numpy: -0.8488930160357633 tensorflow slow: -0.84889317 tensorflow fast: -0.84889317 1 numpy: -7.442875031036973 tensorflow slow: -7.442877 tensorflow fast: -7.442876
优化的数据对数似然
我们可以使用 TFP 的双射函数来构建我们自己的多元正态分布版本。以下是关键思想
假设我有一个列向量 \(X\),其元素是 \(N(0, 1)\) 的独立同分布样本。我们有 \(\text{mean}(X) = 0\) 和 \(\text{cov}(X) = I\)
现在令 \(Y = A X + b\)。我们有 \(\text{mean}(Y) = b\) 和 \(\text{cov}(Y) = A A^T\)
因此,我们可以使用仿射变换 \(Ax+b\) 对独立同分布标准正态样本向量进行变换,从而得到均值为 \(b\) 且协方差为 \(C\) 的向量,前提是 \(A A^T = C\)。\(C\) 的 Cholesky 分解具有所需的属性。但是,还有其他解决方案。
令 \(P = C^{-1}\),并令 \(P\) 的 Cholesky 分解为 \(B\),即 \(B B^T = P\)。现在
\(P^{-1} = (B B^T)^{-1} = B^{-T} B^{-1} = B^{-T} (B^{-T})^T\)
因此,另一种获得我们所需均值和协方差的方法是使用仿射变换 \(Y=B^{-T}X + b\)。
我们的方法(由 此笔记本 提供)
- 使用
tfd.Independent()将一批一维Normal随机变量组合成一个单一的多维随机变量。该reinterpreted_batch_ndims参数用于Independent()指定应重新解释为事件维度的批次维度的数量。在我们的例子中,我们创建了一个长度为 2 的一维批次,将其转换为长度为 2 的一维事件,因此reinterpreted_batch_ndims=1。 - 应用一个双射函数来添加所需的协方差:
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky, adjoint=True))。请注意,在上面,我们将我们的独立同分布正态随机变量乘以精度矩阵的 Cholesky 因子的逆的转置 \((B^{-T}X)\)。该tfb.Invert负责对 \(B\) 进行求逆,而adjoint=True标志执行转置。 - 应用一个双射函数来添加所需的偏移量:
tfb.Shift(shift=shift)请注意,我们必须将偏移量作为与初始求逆仿射变换不同的步骤进行,否则求逆的比例将应用于偏移量(因为 \(y=Ax+b\) 的逆是 \(x=A^{-1}y - A^{-1}b\)).
class MVNPrecisionCholesky(tfd.TransformedDistribution):
"""Multivariate normal parameterized by loc and Cholesky precision matrix."""
def __init__(self, loc, precision_cholesky, name=None):
super(MVNPrecisionCholesky, self).__init__(
distribution=tfd.Independent(
tfd.Normal(loc=tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=precision_cholesky,
adjoint=True)),
]),
name=name)
@tf.function(autograph=False)
def log_lik_data_cholesky(precisions_cholesky, replicated_data):
n = tf.shape(precisions_cholesky)[0] # number of precision matrices
rv_data = MVNPrecisionCholesky(
loc=tf.zeros([n, 2]),
precision_cholesky=precisions_cholesky)
return tf.reduce_sum(rv_data.log_prob(replicated_data), axis=0)
# check against the numpy implementation
true_precision_cholesky = np.linalg.cholesky(true_precision)
precisions = [np.eye(2, dtype=np.float32), true_precision]
precisions_cholesky = np.stack([np.linalg.cholesky(m) for m in precisions])
precisions = np.stack(precisions)
n = precisions_cholesky.shape[0]
replicated_data = np.tile(np.expand_dims(my_data, axis=1), reps=[1, 2, 1])
lik_tf = log_lik_data_cholesky(precisions_cholesky, replicated_data).numpy()
for i in range(n):
print(i)
print('numpy:', log_lik_data_numpy(precisions[i], my_data))
print('tensorflow:', lik_tf[i])
0 numpy: -430.71218815801365 tensorflow: -430.71207 1 numpy: -280.81822950593767 tensorflow: -280.81824
组合的对数似然函数
现在,我们在闭包中组合我们的先验和数据对数似然函数。
def get_log_lik_cholesky(data, n_chains=1):
# The data argument that is passed in will be available to the inner function
# below so it doesn't have to be passed in as a parameter.
replicated_data = np.tile(np.expand_dims(data, axis=1), reps=[1, n_chains, 1])
@tf.function(autograph=False)
def _log_lik_cholesky(precisions_cholesky):
return (log_lik_data_cholesky(precisions_cholesky, replicated_data) +
log_lik_prior_cholesky(precisions_cholesky))
return _log_lik_cholesky
约束双射器
我们的样本被限制为有效的 Cholesky 因子,这意味着它们必须是具有正对角线的下三角矩阵。该 TransformedTransitionKernel 需要一个双射函数,该函数将无约束张量映射到具有我们所需约束的张量。我们已经从双射函数的逆中删除了 Cholesky 分解,这加快了速度。
unconstrained_to_precision_cholesky = tfb.Chain([
# step 2: exponentiate the diagonals
tfb.TransformDiagonal(tfb.Exp(validate_args=VALIDATE_ARGS)),
# step 1: expand the vector to a lower triangular matrix
tfb.FillTriangular(validate_args=VALIDATE_ARGS),
])
# some checks
inv = unconstrained_to_precision_cholesky.inverse(precisions_cholesky).numpy()
fwd = unconstrained_to_precision_cholesky.forward(inv).numpy()
print('precisions_cholesky:\n', precisions_cholesky)
print('\ninv:\n', inv)
print('\nfwd(inv):\n', fwd)
precisions_cholesky: [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]] inv: [[ 0.0000000e+00 0.0000000e+00 0.0000000e+00] [ 3.5762781e-07 -2.0647411e+00 1.3721828e-01]] fwd(inv): [[[ 1. 0. ] [ 0. 1. ]] [[ 1.1470785 0. ] [-2.0647411 1.0000004]]]
初始值
我们生成一个初始值的张量。我们正在使用 Cholesky 因子,因此我们生成一些 Cholesky 因子初始值。
# The number of chains is determined by the shape of the initial values.
# Here we'll generate 3 chains, so we'll need a tensor of 3 initial values.
N_CHAINS = 3
np.random.seed(123)
initial_values_cholesky = []
for i in range(N_CHAINS):
initial_values_cholesky.append(np.array(
[[0.5 + np.random.uniform(), 0.0],
[-0.5 + np.random.uniform(), 0.5 + np.random.uniform()]],
dtype=np.float32))
initial_values_cholesky = np.stack(initial_values_cholesky)
采样
我们使用 TransformedTransitionKernel 对 N_CHAINS 个链进行采样。
@tf.function(autograph=False)
def sample():
tf.random.set_seed(123)
log_lik_fn = get_log_lik_cholesky(my_data)
# Tuning acceptance rates:
dtype = np.float32
num_burnin_iter = 3000
num_warmup_iter = int(0.8 * num_burnin_iter)
num_chain_iter = 2500
# Set the target average acceptance ratio for the HMC as suggested by
# Beskos et al. (2013):
# https://projecteuclid.org/download/pdfview_1/euclid.bj/1383661192
target_accept_rate = 0.651
# Initialize the HMC sampler.
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=log_lik_fn,
step_size=0.01,
num_leapfrog_steps=3)
ttk = tfp.mcmc.TransformedTransitionKernel(
inner_kernel=hmc, bijector=unconstrained_to_precision_cholesky)
# Adapt the step size using standard adaptive MCMC procedure. See Section 4.2
# of Andrieu and Thoms (2008):
# http://www4.ncsu.edu/~rsmith/MA797V_S12/Andrieu08_AdaptiveMCMC_Tutorial.pdf
adapted_kernel = tfp.mcmc.SimpleStepSizeAdaptation(
inner_kernel=ttk,
num_adaptation_steps=num_warmup_iter,
target_accept_prob=target_accept_rate)
states = tfp.mcmc.sample_chain(
num_results=num_chain_iter,
num_burnin_steps=num_burnin_iter,
current_state=initial_values,
kernel=adapted_kernel,
trace_fn=None,
parallel_iterations=1)
# transform samples back to their constrained form
samples = tf.linalg.matmul(states, states, transpose_b=True)
return samples
precision_samples = sample()
收敛性检查
快速收敛性检查看起来不错
r_hat = tfp.mcmc.potential_scale_reduction(precision_samples).numpy()
print(r_hat)
[[1.0013583 1.0019467] [1.0019467 1.0011804]]
将结果与解析后验进行比较
# The output samples have shape [n_steps, n_chains, 2, 2]
# Flatten them to [n_steps * n_chains, 2, 2] via reshape:
precision_samples_reshaped = np.reshape(precision_samples, newshape=[-1, 2, 2])
同样,样本均值和标准差与解析后验的均值和标准差相匹配。
print('True posterior mean:\n', posterior_mean)
print('Mean of samples:\n', np.mean(precision_samples_reshaped, axis=0))
True posterior mean: [[ 0.9641779 -1.6534661] [-1.6534661 3.8683164]] Mean of samples: [[ 0.9668749 -1.6552604] [-1.6552604 3.8676758]]
print('True posterior standard deviation:\n', posterior_sd)
print('Standard deviation of samples:\n', np.std(precision_samples_reshaped, axis=0))
True posterior standard deviation: [[0.13435492 0.25050813] [0.25050813 0.53903675]] Standard deviation of samples: [[0.13329637 0.24913797] [0.24913797 0.53983945]]
好了,都完成了!我们已经让我们的优化采样器正常工作了。
