 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
在本笔记本中,我们将探索 TensorFlow 分布(简称 TFD)。本笔记本的目标是帮助您逐步了解学习曲线,包括了解 TFD 对张量形状的处理方式。本笔记本尝试在抽象概念之前展示示例。我们将首先介绍规范的简单方法,并将最通用的抽象视图留到最后。如果您喜欢更抽象和参考风格的教程,请查看 了解 TensorFlow 分布形状。如果您对这里的内容有任何疑问,请随时联系(或加入)TensorFlow Probability 邮件列表。我们很乐意提供帮助。
在开始之前,我们需要导入相应的库。我们的整体库是 tensorflow_probability。按照惯例,我们通常将分布库称为 tfd。
Tensorflow Eager 是 TensorFlow 的一个命令式执行环境。在 TensorFlow Eager 中,每个 TF 操作都会立即评估并产生结果。这与 TensorFlow 的标准“图”模式形成对比,在标准“图”模式中,TF 操作会将节点添加到稍后执行的图中。整个笔记本都是使用 TF Eager 编写的,尽管这里介绍的概念都不依赖于此,并且 TFP 可以在图模式下使用。
import collections
import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions
try:
tf.compat.v1.enable_eager_execution()
except ValueError:
pass
import matplotlib.pyplot as plt
基本单变量分布
让我们直接开始创建一个正态分布
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
我们可以从中抽取一个样本
n.sample()
<tf.Tensor: shape=(), dtype=float32, numpy=0.25322816>
我们可以抽取多个样本
n.sample(3)
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.4658079, -0.5653636, 0.9314412], dtype=float32)>
我们可以评估对数概率
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
我们可以评估多个对数概率
n.log_prob([0., 2., 4.])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.9189385, -2.9189386, -8.918939 ], dtype=float32)>
我们有各种各样的分布。让我们尝试一个伯努利分布
b = tfd.Bernoulli(probs=0.7)
b
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[] event_shape=[] dtype=int32>
b.sample()
<tf.Tensor: shape=(), dtype=int32, numpy=1>
b.sample(8)
<tf.Tensor: shape=(8,), dtype=int32, numpy=array([1, 0, 0, 0, 1, 0, 1, 0], dtype=int32)>
b.log_prob(1)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.35667497>
b.log_prob([1, 0, 1, 0])
<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.35667497, -1.2039728 , -0.35667497, -1.2039728 ], dtype=float32)>
多变量分布
我们将创建一个具有对角协方差的多元正态分布
nd = tfd.MultivariateNormalDiag(loc=[0., 10.], scale_diag=[1., 4.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
与我们之前创建的单变量正态分布相比,有什么不同?
tfd.Normal(loc=0., scale=1.)
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
我们看到单变量正态分布的 event_shape 为 (),表示它是一个标量分布。多元正态分布的 event_shape 为 2,表示该分布的基本 事件空间 是二维的。
采样与之前一样
nd.sample()
<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.2489667, 15.025171 ], dtype=float32)>
nd.sample(5)
<tf.Tensor: shape=(5, 2), dtype=float32, numpy=
array([[-1.5439653 , 8.9968405 ],
[-0.38730723, 12.448896 ],
[-0.8697963 , 9.330035 ],
[-1.2541095 , 10.268944 ],
[ 2.3475595 , 13.184147 ]], dtype=float32)>
nd.log_prob([0., 10])
<tf.Tensor: shape=(), dtype=float32, numpy=-3.2241714>
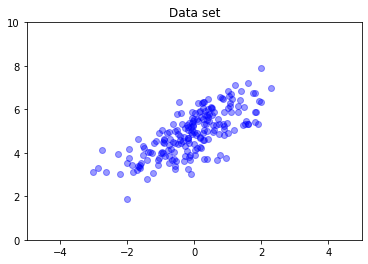
多元正态分布通常不具有对角协方差。TFD 提供了多种创建多元正态分布的方法,包括完全协方差规范(由协方差矩阵的 Cholesky 因子参数化),我们在这里使用它。
covariance_matrix = [[1., .7], [.7, 1.]]
nd = tfd.MultivariateNormalTriL(
loc = [0., 5], scale_tril = tf.linalg.cholesky(covariance_matrix))
data = nd.sample(200)
plt.scatter(data[:, 0], data[:, 1], color='blue', alpha=0.4)
plt.axis([-5, 5, 0, 10])
plt.title("Data set")
plt.show()
多个分布
我们的第一个伯努利分布表示翻转一枚公平的硬币。我们还可以创建一个独立伯努利分布的批次,每个分布都有自己的参数,在一个单独的 Distribution 对象中
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
重要的是要清楚这到底意味着什么。上面的调用定义了三个独立的伯努利分布,它们恰好包含在同一个 Python Distribution 对象中。这三个分布不能单独操作。请注意 batch_shape 是 (3,),表示三个分布的批次,而 event_shape 是 (),表示各个分布具有单变量事件空间。
如果我们调用 sample,我们将从所有三个分布中获取一个样本
b3.sample()
<tf.Tensor: shape=(3,), dtype=int32, numpy=array([0, 1, 1], dtype=int32)>
b3.sample(6)
<tf.Tensor: shape=(6, 3), dtype=int32, numpy=
array([[1, 0, 1],
[0, 1, 1],
[0, 0, 1],
[0, 0, 1],
[0, 0, 1],
[0, 1, 0]], dtype=int32)>
如果我们调用 prob(这与 log_prob 具有相同的形状语义;为了清晰起见,我们在这些小的伯努利示例中使用 prob,尽管在应用程序中通常更喜欢 log_prob),我们可以将一个向量传递给它,并评估每个硬币产生该值的概率
b3.prob([1, 1, 0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.29999998], dtype=float32)>
为什么 API 包含批次形状?从语义上讲,可以通过创建一个分布列表并使用 for 循环对其进行迭代来执行相同的计算(至少在 Eager 模式下,在 TF 图模式下,您需要使用 tf.while 循环)。但是,拥有一个(可能很大)的具有相同参数的分布集非常常见,并且尽可能使用向量化计算是能够使用硬件加速器执行快速计算的关键因素。
使用 Independent 将批次聚合到事件中
在上一节中,我们创建了 b3,一个表示三个硬币抛掷的单个 Distribution 对象。如果我们在向量 \(v\) 上调用 b3.prob,则第 \(i\) 个条目是第 \(i\) 个硬币取值为 \(v[i]\) 的概率。
假设我们想指定一个来自同一底层族的独立随机变量的“联合”分布。从数学上讲,这是一个不同的对象,因为对于这个新的分布,prob 在向量 \(v\) 上将返回一个单一的值,表示所有硬币都与向量 \(v\) 匹配的概率。
我们如何实现这一点?我们使用一个称为 Independent 的“高阶”分布,它接受一个分布并产生一个新的分布,将批次形状移动到事件形状。
b3_joint = tfd.Independent(b3, reinterpreted_batch_ndims=1)
b3_joint
<tfp.distributions.Independent 'IndependentBernoulli' batch_shape=[] event_shape=[3] dtype=int32>
将形状与原始 b3 的形状进行比较。
b3
<tfp.distributions.Bernoulli 'Bernoulli' batch_shape=[3] event_shape=[] dtype=int32>
正如承诺的那样,我们看到 Independent 已将批次形状移动到事件形状:b3_joint 是一个单一分布 (batch_shape = ()),它位于三维事件空间 (event_shape = (3,)) 上。
让我们检查语义。
b3_joint.prob([1, 1, 0])
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999998>
获得相同结果的另一种方法是使用 b3 计算概率,并通过乘法(或者,在更常见的情况下,使用对数概率,则通过求和)手动进行归约。
tf.reduce_prod(b3.prob([1, 1, 0]))
<tf.Tensor: shape=(), dtype=float32, numpy=0.044999994>
Indpendent 允许用户更明确地表示所需的概念。我们认为这非常有用,尽管它并非严格必要。
有趣的事实
b3.sample和b3_joint.sample具有不同的概念实现,但输出不可区分:独立分布的批次与使用Independent从批次创建的单个分布之间的差异在计算概率时出现,而不是在采样时出现。MultivariateNormalDiag可以使用标量Normal和Independent分布进行微不足道的实现(它实际上并非以这种方式实现,但可以实现)。
多元分布的批次
让我们创建一个包含三个全协方差二维多元正态分布的批次。
covariance_matrix = [[[1., .1], [.1, 1.]],
[[1., .3], [.3, 1.]],
[[1., .5], [.5, 1.]]]
nd_batch = tfd.MultivariateNormalTriL(
loc = [[0., 0.], [1., 1.], [2., 2.]],
scale_tril = tf.linalg.cholesky(covariance_matrix))
nd_batch
<tfp.distributions.MultivariateNormalTriL 'MultivariateNormalTriL' batch_shape=[3] event_shape=[2] dtype=float32>
我们看到 batch_shape = (3,),因此有三个独立的多元正态分布,并且 event_shape = (2,),因此每个多元正态分布都是二维的。在这个例子中,各个分布的元素并不独立。
采样有效
nd_batch.sample(4)
<tf.Tensor: shape=(4, 3, 2), dtype=float32, numpy=
array([[[ 0.7367498 , 2.730996 ],
[-0.74080074, -0.36466932],
[ 0.6516018 , 0.9391426 ]],
[[ 1.038303 , 0.12231752],
[-0.94788766, -1.204232 ],
[ 4.059758 , 3.035752 ]],
[[ 0.56903946, -0.06875849],
[-0.35127294, 0.5311631 ],
[ 3.4635801 , 4.565582 ]],
[[-0.15989424, -0.25715637],
[ 0.87479895, 0.97391707],
[ 0.5211419 , 2.32108 ]]], dtype=float32)>
由于 batch_shape = (3,) 且 event_shape = (2,),因此我们将形状为 (3, 2) 的张量传递给 log_prob。
nd_batch.log_prob([[0., 0.], [1., 1.], [2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-1.8328519, -1.7907217, -1.694036 ], dtype=float32)>
广播,又名为什么这如此令人困惑?
抽象出我们到目前为止所做的事情,每个分布都有一个批次形状 B 和一个事件形状 E。令 BE 为事件形状的串联。
- 对于单变量标量分布
n和b,BE = ().。 - 对于二维多元正态分布
nd。BE = (2). - 对于
b3和b3_joint,BE = (3). - 对于多元正态分布的批次
ndb,BE = (3, 2).
我们到目前为止一直在使用的“评估规则”是
- 没有参数的样本返回形状为
BE的张量;使用标量 n 采样返回一个“n 乘BE”的张量。 prob和log_prob接受形状为BE的张量,并返回形状为B的结果。
prob 和 log_prob 的实际“评估规则”更复杂,它提供潜在的强大功能和速度,但也带来复杂性和挑战。实际规则(本质上)是,log_prob 的参数必须与 可广播 的 BE 相对;任何“额外”维度都将保留在输出中。
让我们探索一下含义。对于单变量正态分布 n,BE = (),因此 log_prob 期望一个标量。如果我们将形状不为空的张量传递给 log_prob,则这些形状将作为输出中的批次维度出现。
n = tfd.Normal(loc=0., scale=1.)
n
<tfp.distributions.Normal 'Normal' batch_shape=[] event_shape=[] dtype=float32>
n.log_prob(0.)
<tf.Tensor: shape=(), dtype=float32, numpy=-0.9189385>
n.log_prob([0.])
<tf.Tensor: shape=(1,), dtype=float32, numpy=array([-0.9189385], dtype=float32)>
n.log_prob([[0., 1.], [-1., 2.]])
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[-0.9189385, -1.4189385],
[-1.4189385, -2.9189386]], dtype=float32)>
让我们转向二维多元正态分布 nd(参数已更改以说明目的)。
nd = tfd.MultivariateNormalDiag(loc=[0., 1.], scale_diag=[1., 1.])
nd
<tfp.distributions.MultivariateNormalDiag 'MultivariateNormalDiag' batch_shape=[] event_shape=[2] dtype=float32>
log_prob “期望”一个形状为 (2,) 的参数,但它将接受任何与该形状可广播的参数。
nd.log_prob([0., 0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
但我们可以传入“更多”示例,并一次性评估所有示例的 log_prob。
nd.log_prob([[0., 0.],
[1., 1.],
[2., 2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
也许不太吸引人,我们可以对事件维度进行广播。
nd.log_prob([0.])
<tf.Tensor: shape=(), dtype=float32, numpy=-2.337877>
nd.log_prob([[0.], [1.], [2.]])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-2.337877 , -2.337877 , -4.3378773], dtype=float32)>
以这种方式广播是我们“尽可能启用广播”设计的产物;这种用法有点争议,可能会在 TFP 的未来版本中删除。
现在让我们再次看看三个硬币的例子。
b3 = tfd.Bernoulli(probs=[.3, .5, .7])
在这里,使用广播来表示每个硬币出现正面的概率非常直观。
b3.prob([1])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.29999998, 0.5 , 0.7 ], dtype=float32)>
(将此与 b3.prob([1., 1., 1.]) 进行比较,我们将在介绍 b3 时使用该方法。)
现在假设我们想知道,对于每个硬币,硬币出现正面的概率以及出现反面的概率。我们可以想象尝试
b3.log_prob([0, 1])
不幸的是,这会产生一个错误,并带有很长且不可读的堆栈跟踪。 b3 具有 BE = (3),因此我们必须将 b3.prob 传递给与 (3,) 可广播的内容。 [0, 1] 的形状为 (2),因此它无法广播并产生错误。相反,我们必须说
b3.prob([[0], [1]])
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[0.7, 0.5, 0.3],
[0.3, 0.5, 0.7]], dtype=float32)>
为什么? [[0], [1]] 的形状为 (2, 1),因此它与形状 (3) 可广播,形成 (2, 3) 的广播形状。
广播非常强大:在某些情况下,它可以将使用的内存量减少一个数量级,并且它通常可以使用户代码更短。但是,用它编程可能很困难。如果您调用 log_prob 并收到错误,则几乎总是广播失败导致的问题。
更进一步
在本教程中,我们(希望)提供了一个简单的介绍。以下是一些更进一步的提示。
event_shape、batch_shape和sample_shape可以是任意秩(在本教程中,它们始终是标量或秩 1)。这增加了功能,但同样会导致编程挑战,尤其是在涉及广播时。有关形状操作的更多深入了解,请参阅 理解 TensorFlow 分布形状。- TFP 包含一个强大的抽象,称为
Bijectors,它与TransformedDistribution结合使用,提供了一种灵活的组合方式,可以轻松创建新的分布,这些分布是现有分布的可逆变换。我们很快就会尝试编写有关此方面的教程,但在此期间,请查看 文档
