 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
安装
安装
摘要
在本 colab 中,我们将演示如何在 TensorFlow Probability 中使用变分推理拟合广义线性混合效应模型。
模型族
广义线性混合效应模型 (GLMM) 与广义线性模型 (GLM) 类似,但它们将特定于样本的噪声纳入了预测的线性响应中。这在一定程度上很有用,因为它允许罕见特征与更常见的特征共享信息。
作为生成过程,广义线性混合效应模型 (GLMM) 的特征是
\[ \begin{align} \text{对于 } & r = 1\ldots R: \hspace{2.45cm}\text{#对于每个随机效应组}\\ &\begin{aligned} \text{对于 } &c = 1\ldots |C_r|: \hspace{1.3cm}\text{#对于组 $r$ 的每个类别(“级别”)}\\ &\begin{aligned} \beta_{rc} &\sim \text{多元正态分布}(\text{位置}=0_{D_r}, \text{尺度}=\Sigma_r^{1/2}) \end{aligned} \end{aligned}\\\\ \text{对于 } & i = 1 \ldots N: \hspace{2.45cm}\text{#对于每个样本}\\ &\begin{aligned} &\eta_i = \underbrace{\vphantom{\sum_{r=1}^R}x_i^\top\omega}_\text{固定效应} + \underbrace{\sum_{r=1}^R z_{r,i}^\top \beta_{r,C_r(i) } }_\text{随机效应} \\ &Y_i|x_i,\omega,\{z_{r,i} , \beta_r\}_{r=1}^R \sim \text{分布}(\text{均值}= g^{-1}(\eta_i)) \end{aligned} \end{align} \]
其中
\[ \begin{align} R &= \text{随机效应组的数量}\\ |C_r| &= \text{组 $r$ 的类别数量}\\ N &= \text{训练样本的数量}\\ x_i,\omega &\in \mathbb{R}^{D_0}\\ D_0 &= \text{固定效应的数量}\\ C_r(i) &= \text{第 $i$ 个样本的类别(在组 $r$ 下)}\\ z_{r,i} &\in \mathbb{R}^{D_r}\\ D_r &= \text{与组 $r$ 关联的随机效应的数量}\\ \Sigma_{r} &\in \{S\in\mathbb{R}^{D_r \times D_r} : S \succ 0 \}\\ \eta_i\mapsto g^{-1}(\eta_i) &= \mu_i, \text{逆链接函数}\\ \text{分布} &=\text{仅可由其均值参数化的某种分布} \end{align} \]
换句话说,这意味着每个组的每个类别都与一个样本 \(\beta_{rc}\) 相关,该样本来自多元正态分布。虽然 \(\beta_{rc}\) 抽取始终是独立的,但它们仅对于组 \(r\) 是相同分布的:请注意,对于每个 \(r\in\{1,\ldots,R\}\) 只有一个 \(\Sigma_r\)。
当与样本组的特征 (\(z_{r,i}\)) 进行仿射组合时,结果是第 \(i\) 个预测线性响应(否则为 \(x_i^\top\omega\))上的特定于样本的噪声。
当我们估计 \(\{\Sigma_r:r\in\{1,\ldots,R\}\}\) 时,我们本质上是在估计随机效应组携带的噪声量,否则这些噪声量会淹没 \(x_i^\top\omega\) 中存在的信号。
对于 \(\text{Distribution}\) 和逆链接函数 \(g^{-1}\) 有多种选择。常见选择包括
- \(Y_i\sim\text{Normal}(\text{mean}=\eta_i, \text{scale}=\sigma)\),
- \(Y_i\sim\text{Binomial}(\text{mean}=n_i \cdot \text{sigmoid}(\eta_i), \text{total_count}=n_i)\), 以及,
- \(Y_i\sim\text{Poisson}(\text{mean}=\exp(\eta_i))\).
有关更多可能性,请参阅 tfp.glm 模块。
变分推理
不幸的是,找到参数 \(\beta,\{\Sigma_r\}_r^R\) 的最大似然估计需要一个非解析积分。为了解决这个问题,我们取而代之
- 定义一个参数化分布族(“替代密度”),在附录中表示为 \(q_{\lambda}\)。
- 找到参数 \(\lambda\) 使得 \(q_{\lambda}\) 接近我们的真实目标密度。
分布族将是适当维度的独立高斯分布,而“接近我们的目标密度”的意思是“最小化Kullback-Leibler 散度”。例如,请参阅 “变分推理:统计学家的评论”的第 2.2 节,以获取写得很好的推导和动机。特别是,它表明最小化 K-L 散度等效于最小化负证据下界 (ELBO)。
玩具问题
Gelman 等人 (2007) 的“氡数据集” 是有时用于演示回归方法的数据集。(例如,这篇紧密相关的 PyMC3 博客文章。)氡数据集包含了在整个美国进行的室内氡测量。 氡 是一种天然存在的放射性气体,高浓度时具有毒性。
对于我们的演示,让我们假设我们有兴趣验证这样的假设:含有地下室的家庭中氡含量较高。我们还怀疑氡浓度与土壤类型有关,即地理位置很重要。
为了将此问题构建为机器学习问题,我们将尝试根据读数所在的楼层预测对数氡水平。我们还将使用县作为随机效应,并在此过程中考虑由于地理位置造成的差异。换句话说,我们将使用广义线性混合效应模型。
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import os
from six.moves import urllib
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import pandas as pd
import seaborn as sns; sns.set_context('notebook')
import tensorflow_datasets as tfds
import tensorflow as tf
import tf_keras
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
我们还将快速检查是否有 GPU 可用
if tf.test.gpu_device_name() != '/device:GPU:0':
print("We'll just use the CPU for this run.")
else:
print('Huzzah! Found GPU: {}'.format(tf.test.gpu_device_name()))
We'll just use the CPU for this run.
获取数据集
我们从 TensorFlow 数据集中加载数据集并进行一些简单的预处理。
def load_and_preprocess_radon_dataset(state='MN'):
"""Load the Radon dataset from TensorFlow Datasets and preprocess it.
Following the examples in "Bayesian Data Analysis" (Gelman, 2007), we filter
to Minnesota data and preprocess to obtain the following features:
- `county`: Name of county in which the measurement was taken.
- `floor`: Floor of house (0 for basement, 1 for first floor) on which the
measurement was taken.
The target variable is `log_radon`, the log of the Radon measurement in the
house.
"""
ds = tfds.load('radon', split='train')
radon_data = tfds.as_dataframe(ds)
radon_data.rename(lambda s: s[9:] if s.startswith('feat') else s, axis=1, inplace=True)
df = radon_data[radon_data.state==state.encode()].copy()
df['radon'] = df.activity.apply(lambda x: x if x > 0. else 0.1)
# Make county names look nice.
df['county'] = df.county.apply(lambda s: s.decode()).str.strip().str.title()
# Remap categories to start from 0 and end at max(category).
df['county'] = df.county.astype(pd.api.types.CategoricalDtype())
df['county_code'] = df.county.cat.codes
# Radon levels are all positive, but log levels are unconstrained
df['log_radon'] = df['radon'].apply(np.log)
# Drop columns we won't use and tidy the index
columns_to_keep = ['log_radon', 'floor', 'county', 'county_code']
df = df[columns_to_keep].reset_index(drop=True)
return df
df = load_and_preprocess_radon_dataset()
df.head()
专门化 GLMM 族
在本节中,我们将 GLMM 族专门用于预测氡水平的任务。为此,我们首先考虑 GLMM 的固定效应特殊情况
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j \]
此模型假设观测值 \(j\) 中的对数氡(期望值)由 \(j\) 次读数所在的楼层加上某个常数截距决定。在伪代码中,我们可以写
def estimate_log_radon(floor):
return intercept + floor_effect[floor]
每个楼层都有一个学习到的权重和一个通用的 intercept 项。观察来自 0 层和 1 层的氡测量值,这似乎是一个好的开始
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
df.groupby('floor')['log_radon'].plot(kind='density', ax=ax1);
ax1.set_xlabel('Measured log(radon)')
ax1.legend(title='Floor')
df['floor'].value_counts().plot(kind='bar', ax=ax2)
ax2.set_xlabel('Floor where radon was measured')
ax2.set_ylabel('Count')
fig.suptitle("Distribution of log radon and floors in the dataset");
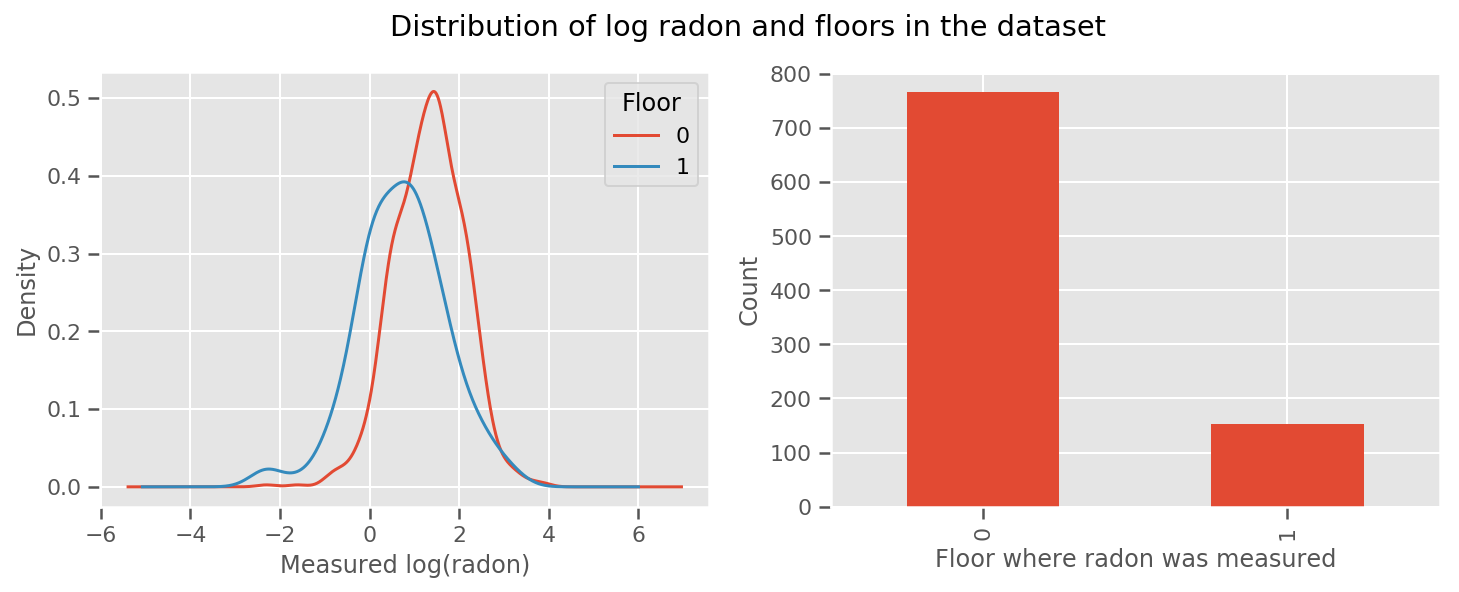
为了使模型更复杂一些,最好包含一些有关地理位置的信息:氡是铀衰变链的一部分,可能存在于地表中,因此地理位置似乎是需要考虑的关键因素。
\[ \mathbb{E}[\log(\text{radon}_j)] = c + \text{floor_effect}_j + \text{county_effect}_j \]
同样,在伪代码中,我们有
def estimate_log_radon(floor, county):
return intercept + floor_effect[floor] + county_effect[county]
与之前相同,只是有一个特定于县的权重。
给定一个足够大的训练集,这是一个合理的模型。但是,根据我们从明尼苏达州获得的数据,我们发现有很多县的测量值很少。例如,85 个县中有 39 个县的观测值少于 5 个。
这促使我们以一种方式在所有观测值之间共享统计强度,随着每个县的观测值数量增加,这种方式会收敛到上述模型。
fig, ax = plt.subplots(figsize=(22, 5));
county_freq = df['county'].value_counts()
county_freq.plot(kind='bar', ax=ax)
ax.set_xlabel('County')
ax.set_ylabel('Number of readings');
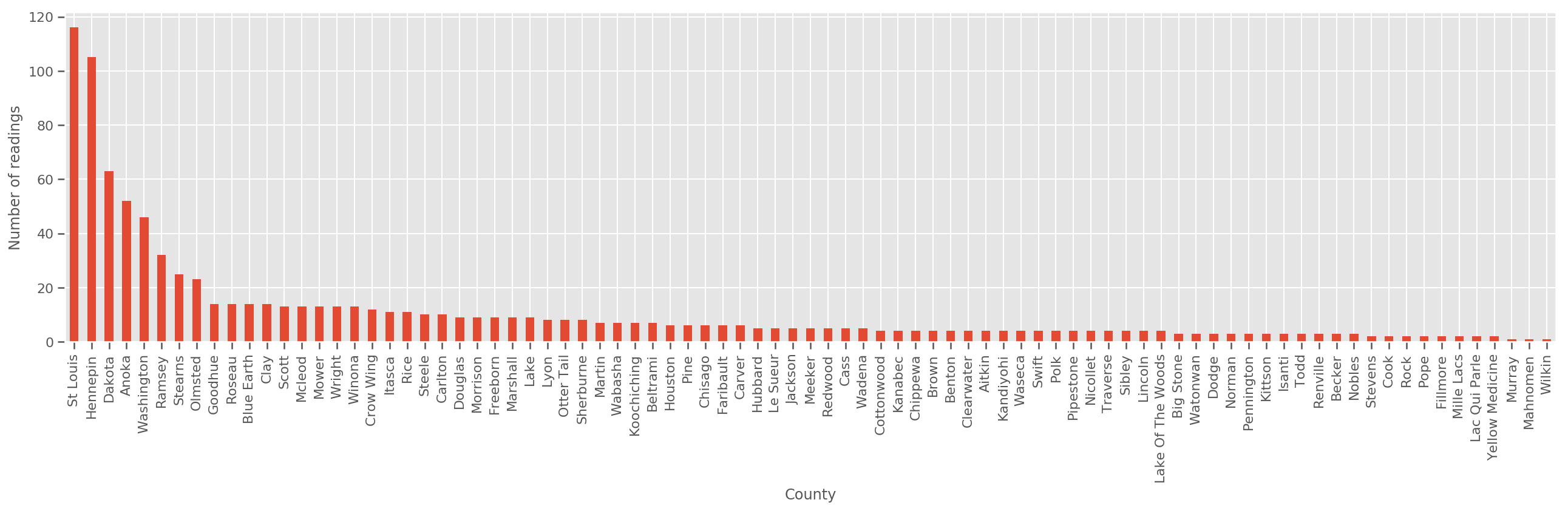
如果我们拟合此模型,county_effect 向量最终可能会记住只有少量训练样本的县的结果,这可能会过度拟合并导致泛化能力差。
GLMM 为上述两个 GLM 提供了一个折中的方案。我们可以考虑拟合
\[ \log(\text{radon}_j) \sim c + \text{floor_effect}_j + \mathcal{N}(\text{county_effect}_j, \text{county_scale}) \]
此模型与第一个模型相同,但我们已将似然度固定为正态分布,并将通过(单个)变量 county_scale 在所有县之间共享方差。在伪代码中,
def estimate_log_radon(floor, county):
county_mean = county_effect[county]
random_effect = np.random.normal() * county_scale + county_mean
return intercept + floor_effect[floor] + random_effect
我们将使用观测数据推断出 county_scale、county_mean 和 random_effect 的联合分布。全局 county_scale 允许我们在各县之间共享统计强度:观测值较多的县为观测值较少的县的方差提供了一个命中。此外,随着我们收集更多数据,此模型将收敛到没有合并比例变量的模型 - 即使使用此数据集,我们也会对使用任一模型观测最多的县得出类似的结论。
实验
我们现在将尝试使用 TensorFlow 中的变分推理拟合上述 GLMM。首先,我们将数据拆分为特征和标签。
features = df[['county_code', 'floor']].astype(int)
labels = df[['log_radon']].astype(np.float32).values.flatten()
指定模型
def make_joint_distribution_coroutine(floor, county, n_counties, n_floors):
def model():
county_scale = yield tfd.HalfNormal(scale=1., name='scale_prior')
intercept = yield tfd.Normal(loc=0., scale=1., name='intercept')
floor_weight = yield tfd.Normal(loc=0., scale=1., name='floor_weight')
county_prior = yield tfd.Normal(loc=tf.zeros(n_counties),
scale=county_scale,
name='county_prior')
random_effect = tf.gather(county_prior, county, axis=-1)
fixed_effect = intercept + floor_weight * floor
linear_response = fixed_effect + random_effect
yield tfd.Normal(loc=linear_response, scale=1., name='likelihood')
return tfd.JointDistributionCoroutineAutoBatched(model)
joint = make_joint_distribution_coroutine(
features.floor.values, features.county_code.values, df.county.nunique(),
df.floor.nunique())
# Define a closure over the joint distribution
# to condition on the observed labels.
def target_log_prob_fn(*args):
return joint.log_prob(*args, likelihood=labels)
指定代理后验
我们现在将代理族 \(q_{\lambda}\) 放在一起,其中参数 \(\lambda\) 是可训练的。在这种情况下,我们的族是独立的多元正态分布,每个参数一个,并且 \(\lambda = \{(\mu_j, \sigma_j)\}\),其中 \(j\) 索引四个参数。
我们用于拟合代理族的算法使用 tf.Variables。我们还使用 tfp.util.TransformedVariable 以及 Softplus 来约束(可训练的)比例参数为正。此外,我们对整个 scale_prior 应用 Softplus,这是一个正参数。
我们使用一些抖动初始化这些可训练变量以帮助优化。
# Initialize locations and scales randomly with `tf.Variable`s and
# `tfp.util.TransformedVariable`s.
_init_loc = lambda shape=(): tf.Variable(
tf.random.uniform(shape, minval=-2., maxval=2.))
_init_scale = lambda shape=(): tfp.util.TransformedVariable(
initial_value=tf.random.uniform(shape, minval=0.01, maxval=1.),
bijector=tfb.Softplus())
n_counties = df.county.nunique()
surrogate_posterior = tfd.JointDistributionSequentialAutoBatched([
tfb.Softplus()(tfd.Normal(_init_loc(), _init_scale())), # scale_prior
tfd.Normal(_init_loc(), _init_scale()), # intercept
tfd.Normal(_init_loc(), _init_scale()), # floor_weight
tfd.Normal(_init_loc([n_counties]), _init_scale([n_counties]))]) # county_prior
请注意,此单元格可以用 tfp.experimental.vi.build_factored_surrogate_posterior 替换,如下所示
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=joint.event_shape_tensor()[:-1],
constraining_bijectors=[tfb.Softplus(), None, None, None])
结果
请记住,我们的目标是定义一个易于处理的参数化分布族,然后选择参数,以便我们有一个接近目标分布的易于处理的分布。
我们在上面构建了代理分布,并且可以使用 tfp.vi.fit_surrogate_posterior,它接受一个优化器和给定的步数来找到代理模型的参数,从而最大程度地减少负 ELBO(对应于最小化代理分布和目标分布之间的 Kullback-Liebler 散度)。
返回值是每个步骤的负 ELBO,并且 surrogate_posterior 中的分布将使用优化器找到的参数进行更新。
optimizer = tf_keras.optimizers.Adam(learning_rate=1e-2)
losses = tfp.vi.fit_surrogate_posterior(
target_log_prob_fn,
surrogate_posterior,
optimizer=optimizer,
num_steps=3000,
seed=42,
sample_size=2)
(scale_prior_,
intercept_,
floor_weight_,
county_weights_), _ = surrogate_posterior.sample_distributions()
print(' intercept (mean): ', intercept_.mean())
print(' floor_weight (mean): ', floor_weight_.mean())
print(' scale_prior (approx. mean): ', tf.reduce_mean(scale_prior_.sample(10000)))
intercept (mean): tf.Tensor(1.4352839, shape=(), dtype=float32)
floor_weight (mean): tf.Tensor(-0.6701997, shape=(), dtype=float32)
scale_prior (approx. mean): tf.Tensor(0.28682157, shape=(), dtype=float32)
fig, ax = plt.subplots(figsize=(10, 3))
ax.plot(losses, 'k-')
ax.set(xlabel="Iteration",
ylabel="Loss (ELBO)",
title="Loss during training",
ylim=0);
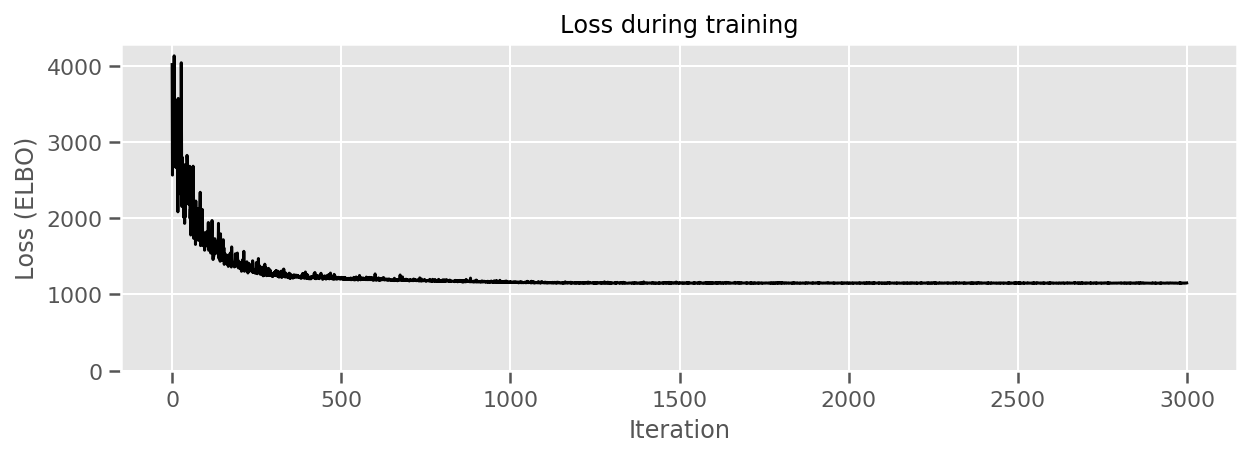
我们可以绘制估计的县级平均值效果,以及该平均值的不确定性。我们按观察次数对其进行排序,其中观察次数最多的在左侧。请注意,对于观察次数多的县,不确定性很小,但对于仅有一两次观察的县,不确定性更大。
county_counts = (df.groupby(by=['county', 'county_code'], observed=True)
.agg('size')
.sort_values(ascending=False)
.reset_index(name='count'))
means = county_weights_.mean()
stds = county_weights_.stddev()
fig, ax = plt.subplots(figsize=(20, 5))
for idx, row in county_counts.iterrows():
mid = means[row.county_code]
std = stds[row.county_code]
ax.vlines(idx, mid - std, mid + std, linewidth=3)
ax.plot(idx, means[row.county_code], 'ko', mfc='w', mew=2, ms=7)
ax.set(
xticks=np.arange(len(county_counts)),
xlim=(-1, len(county_counts)),
ylabel="County effect",
title=r"Estimates of county effects on log radon levels. (mean $\pm$ 1 std. dev.)",
)
ax.set_xticklabels(county_counts.county, rotation=90);
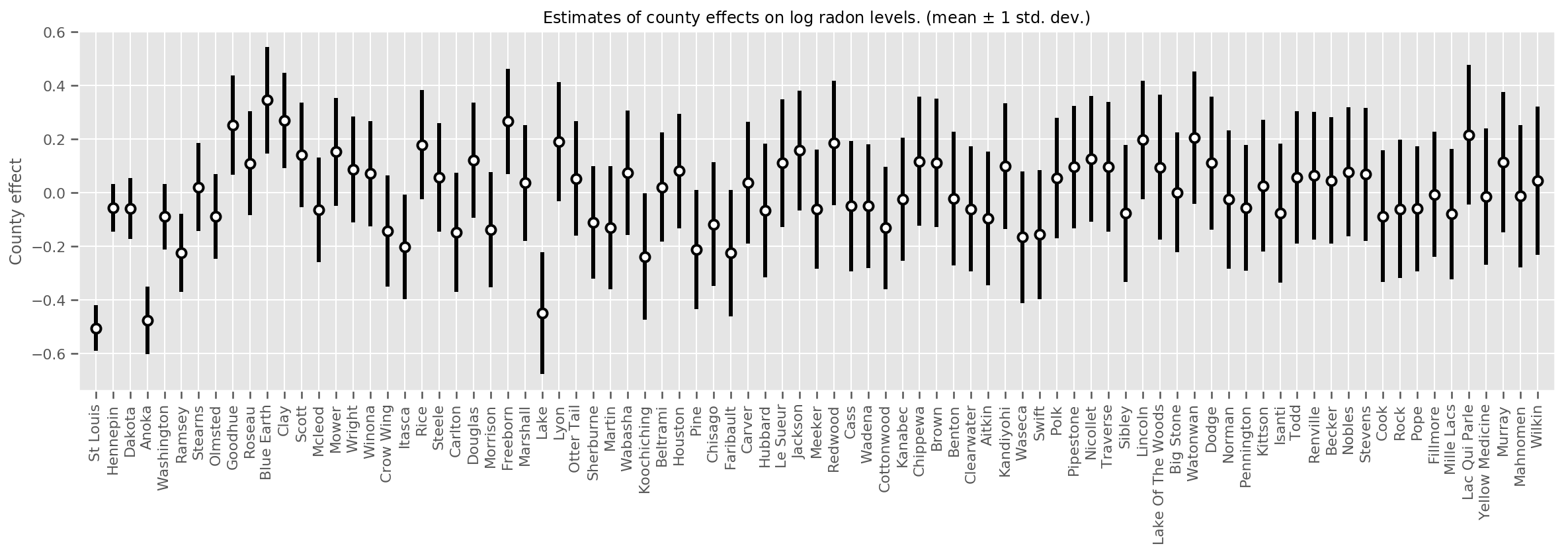
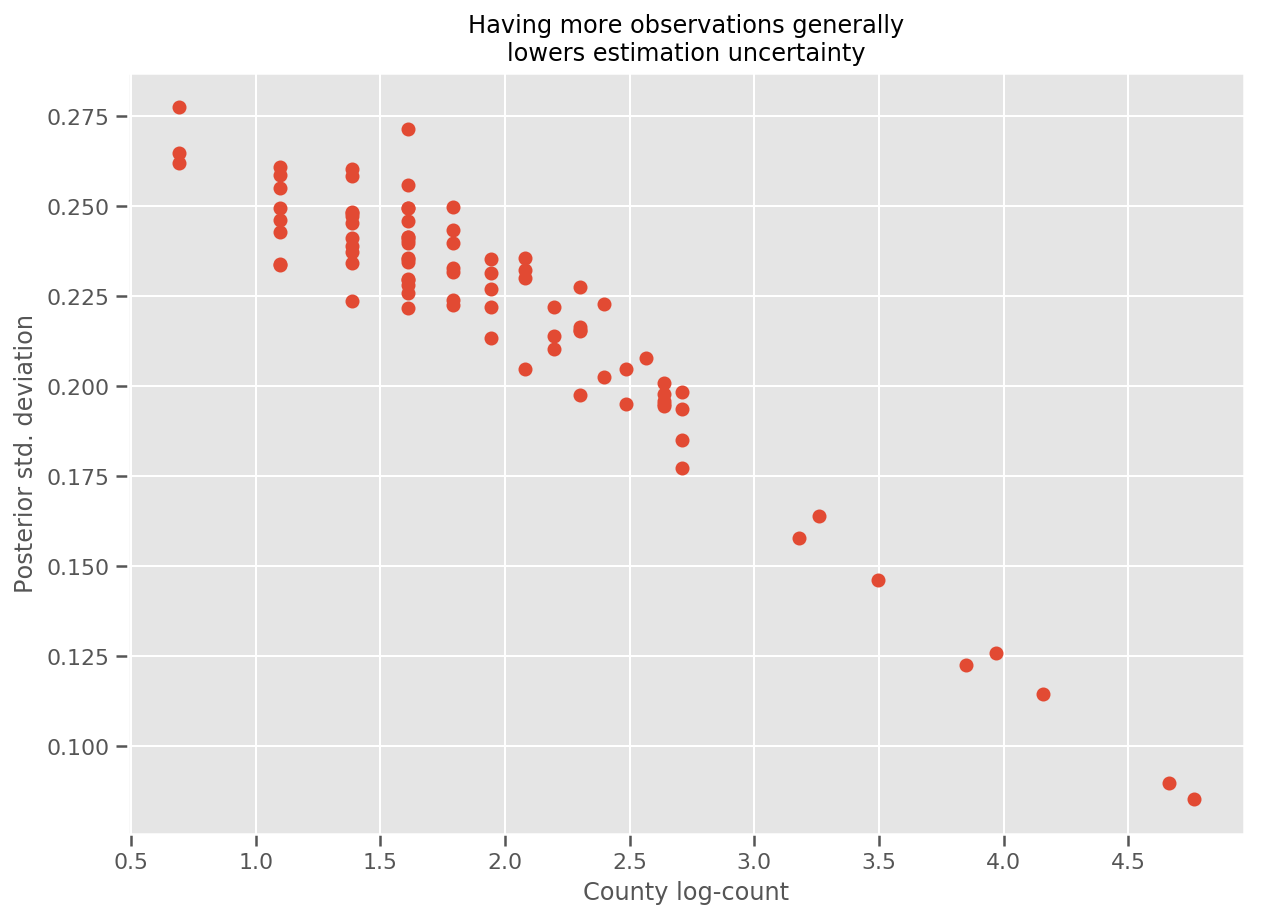
实际上,我们可以通过绘制观察次数的对数与估计标准差的关系,更直接地看到这一点,并看到这种关系近似为线性关系。
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(np.log1p(county_counts['count']), stds.numpy()[county_counts.county_code], 'o')
ax.set(
ylabel='Posterior std. deviation',
xlabel='County log-count',
title='Having more observations generally\nlowers estimation uncertainty'
);
与 R 中的 lme4 进行比较
%%shell
exit # Trick to make this block not execute.
radon = read.csv('srrs2.dat', header = TRUE)
radon = radon[radon$state=='MN',]
radon$radon = ifelse(radon$activity==0., 0.1, radon$activity)
radon$log_radon = log(radon$radon)
# install.packages('lme4')
library(lme4)
fit <- lmer(log_radon ~ 1 + floor + (1 | county), data=radon)
fit
# Linear mixed model fit by REML ['lmerMod']
# Formula: log_radon ~ 1 + floor + (1 | county)
# Data: radon
# REML criterion at convergence: 2171.305
# Random effects:
# Groups Name Std.Dev.
# county (Intercept) 0.3282
# Residual 0.7556
# Number of obs: 919, groups: county, 85
# Fixed Effects:
# (Intercept) floor
# 1.462 -0.693
<IPython.core.display.Javascript at 0x7f90b888e9b0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90bce1dfd0> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780> <IPython.core.display.Javascript at 0x7f90b888e780>
下表总结了结果。
print(pd.DataFrame(data=dict(intercept=[1.462, tf.reduce_mean(intercept_.mean()).numpy()],
floor=[-0.693, tf.reduce_mean(floor_weight_.mean()).numpy()],
scale=[0.3282, tf.reduce_mean(scale_prior_.sample(10000)).numpy()]),
index=['lme4', 'vi']))
intercept floor scale lme4 1.462000 -0.6930 0.328200 vi 1.435284 -0.6702 0.287251
此表表明,VI 结果在 lme4 的 ~10% 范围内。这有点令人惊讶,因为
lme4基于 拉普拉斯方法(而非 VI),- 此协作中未做出实际收敛的努力,
- 为调整超参数做出的努力很小,
- 未采取任何措施对数据进行正则化或预处理(例如,中心特征等)。
结论
在此协作中,我们描述了广义线性混合效应模型,并展示了如何使用 TensorFlow Probability 的变分推理来拟合这些模型。尽管玩具问题只有几百个训练样本,但此处使用的方法与大规模所需的方法相同。
