在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
此笔记本演示了如何使用 TFP 近似推理工具在使用结构化时间序列 (STS) 模型进行拟合和预测时,将(非高斯)观测模型纳入其中。在本例中,我们将使用泊松观测模型来处理离散计数数据。
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import tf_keras
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
合成数据
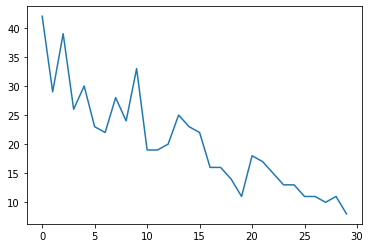
首先,我们将生成一些合成计数数据
num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps))
observed_counts = observed_counts.astype(np.float32)
plt.plot(observed_counts)
[<matplotlib.lines.Line2D at 0x7f940ae958d0>]
模型
我们将指定一个简单的模型,该模型具有随机游走的线性趋势
def build_model(approximate_unconstrained_rates):
trend = tfp.sts.LocalLinearTrend(
observed_time_series=approximate_unconstrained_rates)
return tfp.sts.Sum([trend],
observed_time_series=approximate_unconstrained_rates)
此模型不会对观测到的时间序列进行操作,而是对控制观测的泊松速率参数序列进行操作。
由于泊松速率必须为正,因此我们将使用双射器将实值 STS 模型转换为正值分布。 Softplus 变换 \(y = \log(1 + \exp(x))\) 是一个自然选择,因为它对于正值几乎是线性的,但其他选择(例如 Exp(它将正态随机游走转换为对数正态随机游走))也是可能的。
positive_bijector = tfb.Softplus() # Or tfb.Exp()
# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)
要对非高斯观测模型使用近似推理,我们将 STS 模型编码为 TFP JointDistribution。此联合分布中的随机变量是 STS 模型的参数、潜在泊松速率的时间序列以及观测到的计数。
def sts_with_poisson_likelihood_model():
# Encode the parameters of the STS model as random variables.
param_vals = []
for param in sts_model.parameters:
param_val = yield param.prior
param_vals.append(param_val)
# Use the STS model to encode the log- (or inverse-softplus)
# rate of a Poisson.
unconstrained_rate = yield sts_model.make_state_space_model(
num_timesteps, param_vals)
rate = positive_bijector.forward(unconstrained_rate[..., 0])
observed_counts = yield tfd.Poisson(rate, name='observed_counts')
model = tfd.JointDistributionCoroutineAutoBatched(sts_with_poisson_likelihood_model)
推理准备
我们希望根据观测到的计数推断模型中未观测到的量。首先,我们将联合对数密度条件化为观测到的计数。
pinned_model = model.experimental_pin(observed_counts=observed_counts)
我们还需要一个约束双射器,以确保推理尊重 STS 模型参数的约束(例如,比例必须为正)。
constraining_bijector = pinned_model.experimental_default_event_space_bijector()
使用 HMC 进行推理
我们将使用 HMC(特别是 NUTS)从模型参数和潜在速率的联合后验中采样。
这将比使用 HMC 拟合标准 STS 模型慢得多,因为除了模型的(相对较少的)参数外,我们还必须推断整个泊松速率序列。因此,我们将运行相对较少的步骤;对于推理质量至关重要的应用程序,可能需要增加这些值或运行多个链。
采样器配置
首先,我们指定一个采样器,然后使用 sample_chain 运行该采样内核以生成样本。
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=pinned_model.unnormalized_log_prob,
step_size=0.1),
bijector=constraining_bijector)
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=0.75)
initial_state = constraining_bijector.forward(
type(pinned_model.event_shape)(
*(tf.random.normal(part_shape)
for part_shape in constraining_bijector.inverse_event_shape(
pinned_model.event_shape))))
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps,
trace_fn=None)
t0 = time.time()
samples = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 24.83s.
我们可以通过检查参数轨迹来对推理进行合理性检查。在这种情况下,它们似乎探索了数据的多种解释,这很好,尽管需要更多样本才能判断链的混合程度。
f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
ax.plot(samples[i])
ax.set_title("{} samples".format(param.name))

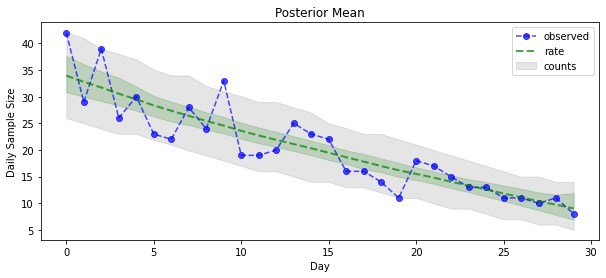
现在是收获的时候了:让我们看看泊松速率的后验!我们还将绘制观测计数的 80% 预测区间,并可以检查此区间是否包含我们实际观测到的约 80% 的计数。
param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples),
[10, 90], axis=0)
_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()
<matplotlib.legend.Legend at 0x7f93ffd35550>
预测
要预测观测到的计数,我们将使用标准 STS 工具构建对潜在速率的预测分布(在无约束空间中,因为 STS 被设计为对实值数据进行建模),然后将采样的预测传递给泊松观测模型
def sample_forecasted_counts(sts_model, posterior_latent_rates,
posterior_params, num_steps_forecast,
num_sampled_forecasts):
# Forecast the future latent unconstrained rates, given the inferred latent
# unconstrained rates and parameters.
unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
observed_time_series=unconstrained_rate_samples,
parameter_samples=posterior_params,
num_steps_forecast=num_steps_forecast)
# Transform the forecast to positive-valued Poisson rates.
rates_forecast_dist = tfd.TransformedDistribution(
unconstrained_rates_forecast_dist,
positive_bijector)
# Sample from the forecast model following the chain rule:
# P(counts) = P(counts | latent_rates)P(latent_rates)
sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()
return sampled_forecast_counts, sampled_latent_rates
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
def plot_forecast_helper(data, forecast_samples, CI=90):
"""Plot the observed time series alongside the forecast."""
plt.figure(figsize=(10, 4))
forecast_median = np.median(forecast_samples, axis=0)
num_steps = len(data)
num_steps_forecast = forecast_median.shape[-1]
plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
label='Observed Data', alpha=0.7)
forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)
CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)
plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
label=str(CI) + '% Forecast Interval', alpha=0.7)
plt.fill_between(forecast_steps,
lower,
upper, color='orange', alpha=0.2)
plt.xlim([0, num_steps+num_steps_forecast])
ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
yrange = ymax-ymin
plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.legend()
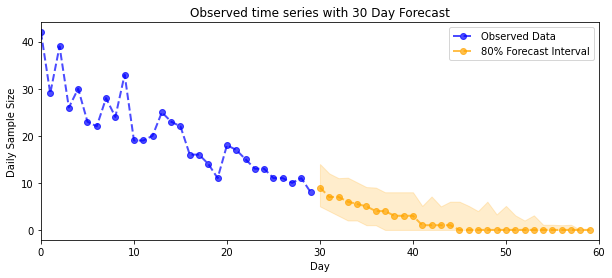
plot_forecast_helper(observed_counts, forecast_samples, CI=80)
VI 推理
变分推断在推断完整时间序列(如我们的近似计数,而不是像标准 STS 模型那样仅仅推断时间序列的参数)时可能存在问题。标准假设变量具有独立的后验分布是错误的,因为每个时间步都与其相邻时间步相关联,这会导致低估不确定性。因此,对于完整时间序列的近似推断,HMC 可能是更好的选择。然而,VI 速度可能快得多,并且可能对模型原型设计或其性能经验证明“足够好”的情况有用。
为了使用 VI 拟合我们的模型,我们只需构建和优化一个代理后验分布
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=pinned_model.event_shape,
bijector=constraining_bijector)
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 1000 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(pinned_model.unnormalized_log_prob,
surrogate_posterior,
optimizer=tf_keras.optimizers.Adam(0.1),
num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
Inference ran in 11.37s.
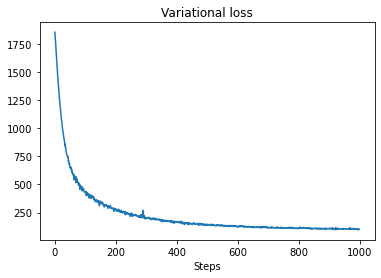
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")
posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
np.random.poisson(rate_samples), [10, 90], axis=0)
_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
label='counts', alpha=0.2)
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
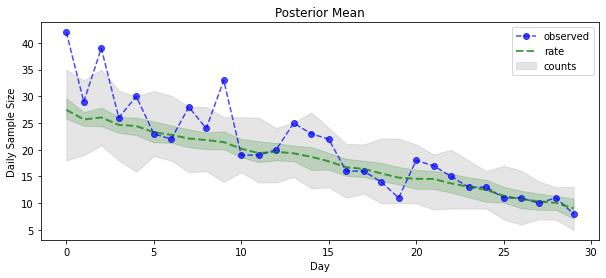
plt.title('Posterior Mean')
plt.legend()
<matplotlib.legend.Legend at 0x7f93ff4735c0>
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
forecast_samples = np.squeeze(forecast_samples)
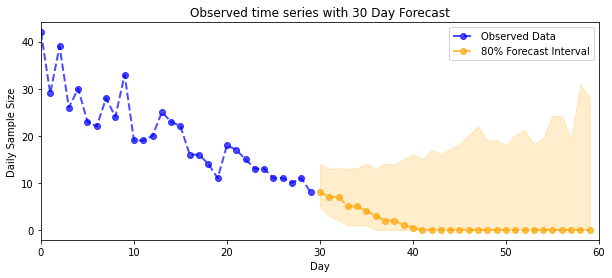
plot_forecast_helper(observed_counts, forecast_samples, CI=80)