 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
八所学校问题 (Rubin 1981) 考虑了在八所学校同时进行的 SAT 辅导项目的有效性。它已成为一个经典问题 (贝叶斯数据分析,Stan),它说明了分层建模在可交换组之间共享信息的用处。
下面的实现是对 Edward 1.0 教程 的改编。
导入
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
import warnings
tf.enable_v2_behavior()
plt.style.use("ggplot")
warnings.filterwarnings('ignore')
数据
来自贝叶斯数据分析,第 5.5 节 (Gelman 等人 2013)
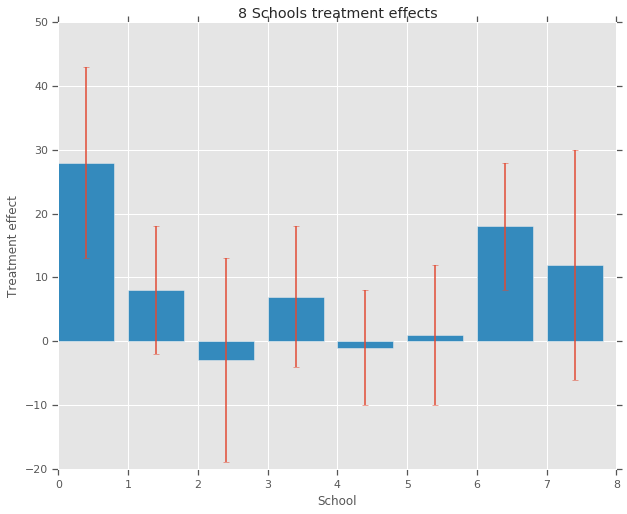
对教育考试服务进行了一项研究,以分析八所高中中 SAT-V(学术能力测验 - 词汇)特殊辅导项目的效用。每项研究中的结果变量是 SAT-V 特殊管理的得分,这是由教育考试服务管理的标准化多项选择测试,用于帮助大学做出录取决定;分数可以在 200 到 800 之间变化,平均值约为 500,标准差约为 100。SAT 考试旨在抵御专门针对提高考试成绩的短期努力;相反,它们旨在反映多年教育积累的知识和能力。然而,本研究中的八所学校都认为其短期辅导项目在提高 SAT 成绩方面非常成功。此外,事先没有理由相信八个项目中的任何一个比其他任何一个更有效,或者某些项目在效果上比其他任何一个更相似。
对于八所学校中的每一所(\(J = 8\),我们有一个估计的治疗效果 \(y_j\) 和一个效果估计的标准误差 \(\sigma_j\)。研究中的治疗效果是通过使用 PSAT-M 和 PSAT-V 分数作为控制变量对治疗组进行线性回归获得的。由于事先没有理由相信任何学校更相似或更不相似,或者任何辅导项目更有效,我们可以将治疗效果视为 可交换的。
num_schools = 8 # number of schools
treatment_effects = np.array(
[28, 8, -3, 7, -1, 1, 18, 12], dtype=np.float32) # treatment effects
treatment_stddevs = np.array(
[15, 10, 16, 11, 9, 11, 10, 18], dtype=np.float32) # treatment SE
fig, ax = plt.subplots()
plt.bar(range(num_schools), treatment_effects, yerr=treatment_stddevs)
plt.title("8 Schools treatment effects")
plt.xlabel("School")
plt.ylabel("Treatment effect")
fig.set_size_inches(10, 8)
plt.show()
模型
为了捕捉数据,我们使用分层正态模型。它遵循生成过程,
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i \sim \text{Normal}\left(\text{loc}{=}\mu,\ \text{scale}{=}\tau \right) \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
其中 \(\mu\) 代表先验平均治疗效果,\(\tau\) 控制学校之间存在多少方差。\(y_i\) 和 \(\sigma_i\) 是观察到的。当 \(\tau \rightarrow \infty\) 时,模型接近无池化模型,即每个学校治疗效果估计都被允许更加独立。当 \(\tau \rightarrow 0\) 时,模型接近完全池化模型,即所有学校的治疗效果都更接近群体平均值 \(\mu\)。为了限制标准差为正数,我们从对数正态分布中抽取 \(\tau\)(这等效于从正态分布中抽取 \(log(\tau)\))。
遵循 使用发散诊断有偏推断,我们将上面的模型转换为等效的非中心模型
\[ \begin{align*} \mu &\sim \text{Normal}(\text{loc}{=}0,\ \text{scale}{=}10) \\ \log\tau &\sim \text{Normal}(\text{loc}{=}5,\ \text{scale}{=}1) \\ \text{for } & i=1\ldots 8:\\ & \theta_i' \sim \text{Normal}\left(\text{loc}{=}0,\ \text{scale}{=}1 \right) \\ & \theta_i = \mu + \tau \theta_i' \\ & y_i \sim \text{Normal}\left(\text{loc}{=}\theta_i,\ \text{scale}{=}\sigma_i \right) \end{align*} \]
我们将此模型具体化为 JointDistributionSequential 实例
model = tfd.JointDistributionSequential([
tfd.Normal(loc=0., scale=10., name="avg_effect"), # `mu` above
tfd.Normal(loc=5., scale=1., name="avg_stddev"), # `log(tau)` above
tfd.Independent(tfd.Normal(loc=tf.zeros(num_schools),
scale=tf.ones(num_schools),
name="school_effects_standard"), # `theta_prime`
reinterpreted_batch_ndims=1),
lambda school_effects_standard, avg_stddev, avg_effect: (
tfd.Independent(tfd.Normal(loc=(avg_effect[..., tf.newaxis] +
tf.exp(avg_stddev[..., tf.newaxis]) *
school_effects_standard), # `theta` above
scale=treatment_stddevs),
name="treatment_effects", # `y` above
reinterpreted_batch_ndims=1))
])
def target_log_prob_fn(avg_effect, avg_stddev, school_effects_standard):
"""Unnormalized target density as a function of states."""
return model.log_prob((
avg_effect, avg_stddev, school_effects_standard, treatment_effects))
贝叶斯推理
给定数据,我们执行哈密顿蒙特卡罗 (HMC) 来计算模型参数的后验分布。
num_results = 5000
num_burnin_steps = 3000
# Improve performance by tracing the sampler using `tf.function`
# and compiling it using XLA.
@tf.function(autograph=False, jit_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
num_results=num_results,
num_burnin_steps=num_burnin_steps,
current_state=[
tf.zeros([], name='init_avg_effect'),
tf.zeros([], name='init_avg_stddev'),
tf.ones([num_schools], name='init_school_effects_standard'),
],
kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.4,
num_leapfrog_steps=3))
states, kernel_results = do_sampling()
avg_effect, avg_stddev, school_effects_standard = states
school_effects_samples = (
avg_effect[:, np.newaxis] +
np.exp(avg_stddev)[:, np.newaxis] * school_effects_standard)
num_accepted = np.sum(kernel_results.is_accepted)
print('Acceptance rate: {}'.format(num_accepted / num_results))
Acceptance rate: 0.5974
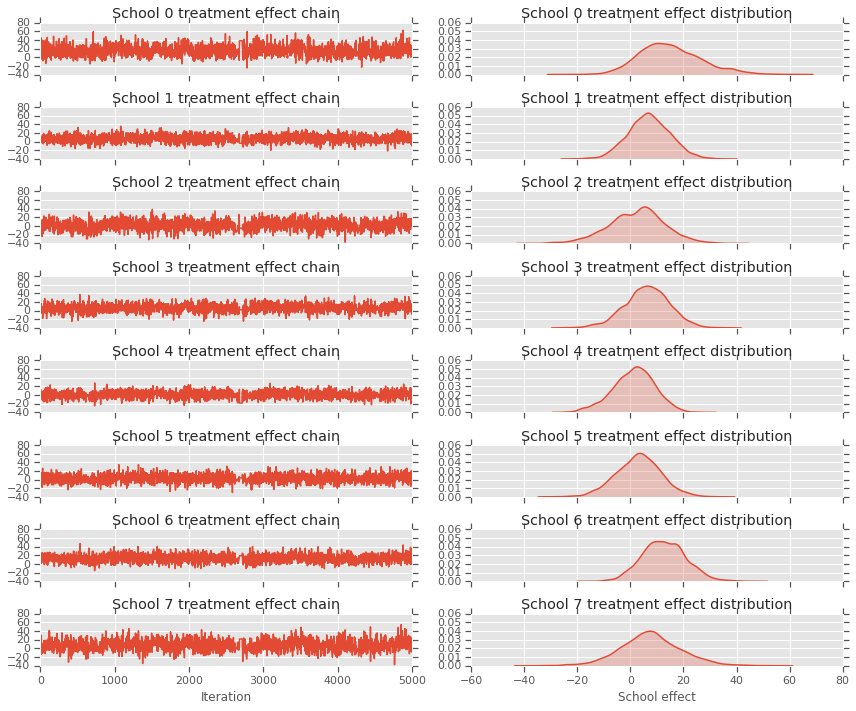
fig, axes = plt.subplots(8, 2, sharex='col', sharey='col')
fig.set_size_inches(12, 10)
for i in range(num_schools):
axes[i][0].plot(school_effects_samples[:,i].numpy())
axes[i][0].title.set_text("School {} treatment effect chain".format(i))
sns.kdeplot(school_effects_samples[:,i].numpy(), ax=axes[i][1], shade=True)
axes[i][1].title.set_text("School {} treatment effect distribution".format(i))
axes[num_schools - 1][0].set_xlabel("Iteration")
axes[num_schools - 1][1].set_xlabel("School effect")
fig.tight_layout()
plt.show()
print("E[avg_effect] = {}".format(np.mean(avg_effect)))
print("E[avg_stddev] = {}".format(np.mean(avg_stddev)))
print("E[school_effects_standard] =")
print(np.mean(school_effects_standard[:, ]))
print("E[school_effects] =")
print(np.mean(school_effects_samples[:, ], axis=0))
E[avg_effect] = 5.57183933258 E[avg_stddev] = 2.47738981247 E[school_effects_standard] = 0.08509017 E[school_effects] = [15.0051 7.103311 2.4552586 6.2744603 1.3364682 3.1125953 12.762501 7.743602 ]
# Compute the 95% interval for school_effects
school_effects_low = np.array([
np.percentile(school_effects_samples[:, i], 2.5) for i in range(num_schools)
])
school_effects_med = np.array([
np.percentile(school_effects_samples[:, i], 50) for i in range(num_schools)
])
school_effects_hi = np.array([
np.percentile(school_effects_samples[:, i], 97.5)
for i in range(num_schools)
])
fig, ax = plt.subplots(nrows=1, ncols=1, sharex=True)
ax.scatter(np.array(range(num_schools)), school_effects_med, color='red', s=60)
ax.scatter(
np.array(range(num_schools)) + 0.1, treatment_effects, color='blue', s=60)
plt.plot([-0.2, 7.4], [np.mean(avg_effect),
np.mean(avg_effect)], 'k', linestyle='--')
ax.errorbar(
np.array(range(8)),
school_effects_med,
yerr=[
school_effects_med - school_effects_low,
school_effects_hi - school_effects_med
],
fmt='none')
ax.legend(('avg_effect', 'HMC', 'Observed effect'), fontsize=14)
plt.xlabel('School')
plt.ylabel('Treatment effect')
plt.title('HMC estimated school treatment effects vs. observed data')
fig.set_size_inches(10, 8)
plt.show()
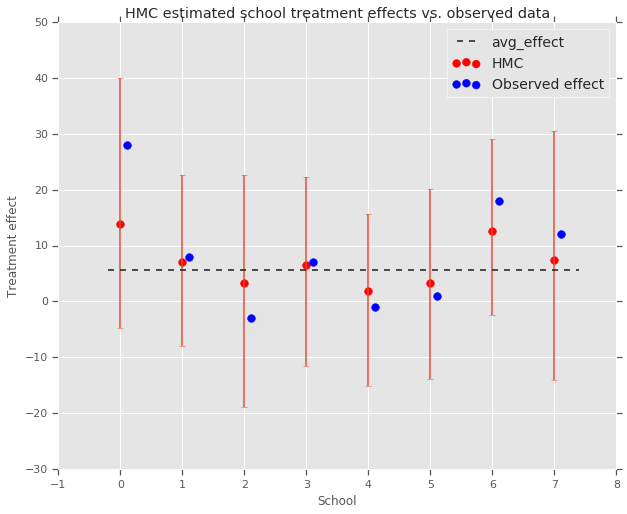
我们可以观察到上述群体 avg_effect 的收缩。
print("Inferred posterior mean: {0:.2f}".format(
np.mean(school_effects_samples[:,])))
print("Inferred posterior mean se: {0:.2f}".format(
np.std(school_effects_samples[:,])))
Inferred posterior mean: 6.97 Inferred posterior mean se: 10.41
批评
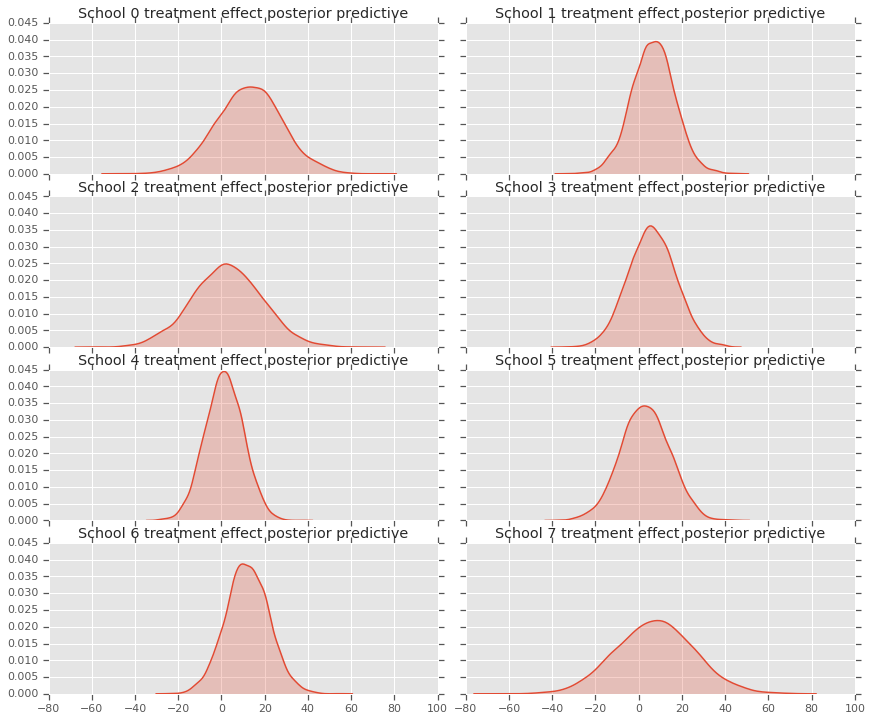
为了获得后验预测分布,即给定观察数据 \(y\) 的新数据 \(y^*\) 的模型
\[ p(y^*|y) \propto \int_\theta p(y^* | \theta)p(\theta |y)d\theta\]
我们将模型中随机变量的值覆盖为设置为后验分布的均值,并从该模型中采样以生成新数据 \(y^*\)。
sample_shape = [5000]
_, _, _, predictive_treatment_effects = model.sample(
value=(tf.broadcast_to(np.mean(avg_effect, 0), sample_shape),
tf.broadcast_to(np.mean(avg_stddev, 0), sample_shape),
tf.broadcast_to(np.mean(school_effects_standard, 0),
sample_shape + [num_schools]),
None))
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(predictive_treatment_effects[:, 2*i].numpy(),
ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect posterior predictive".format(2*i))
sns.kdeplot(predictive_treatment_effects[:, 2*i + 1].numpy(),
ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect posterior predictive".format(2*i + 1))
plt.show()
# The mean predicted treatment effects for each of the eight schools.
prediction = np.mean(predictive_treatment_effects, axis=0)
我们可以查看治疗效果数据与模型后验预测之间的残差。这些对应于上面的图,该图显示了估计效果向总体平均值的收缩。
treatment_effects - prediction
array([14.905351 , 1.2838383, -5.6966295, 0.8327627, -2.3356671,
-2.0363257, 5.997898 , 4.3731265], dtype=float32)
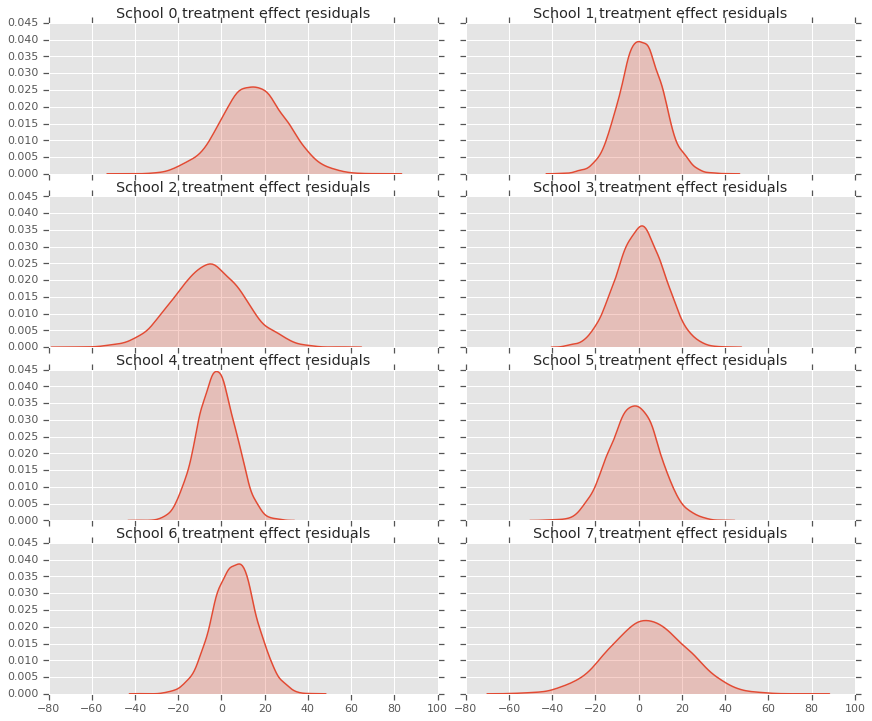
由于我们对每个学校都有一个预测分布,因此我们也可以考虑残差的分布。
residuals = treatment_effects - predictive_treatment_effects
fig, axes = plt.subplots(4, 2, sharex=True, sharey=True)
fig.set_size_inches(12, 10)
fig.tight_layout()
for i, ax in enumerate(axes):
sns.kdeplot(residuals[:, 2*i].numpy(), ax=ax[0], shade=True)
ax[0].title.set_text(
"School {} treatment effect residuals".format(2*i))
sns.kdeplot(residuals[:, 2*i + 1].numpy(), ax=ax[1], shade=True)
ax[1].title.set_text(
"School {} treatment effect residuals".format(2*i + 1))
plt.show()
致谢
本教程最初是用 Edward 1.0 编写的(源代码)。我们感谢所有为编写和修订该版本做出贡献的人。
参考文献
- Donald B. Rubin. 平行随机实验中的估计。教育统计学杂志,6(4):377-401, 1981。
- Andrew Gelman, John Carlin, Hal Stern, David Dunson, Aki Vehtari 和 Donald Rubin。贝叶斯数据分析,第三版。Chapman 和 Hall/CRC,2013。
