 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
线性混合效应模型是一种对结构化线性关系进行建模的简单方法(Harville,1997;Laird 和 Ware,1982)。每个数据点都包含不同类型的输入(分为组),以及一个实值输出。线性混合效应模型是一个分层模型:它在组之间共享统计强度,以改进对任何单个数据点的推断。
在本教程中,我们将使用 TensorFlow Probability 中的实际示例演示线性混合效应模型。我们将使用 JointDistributionCoroutine 和马尔可夫链蒙特卡罗 (tfp.mcmc) 模块。
依赖项和先决条件
导入和设置
加快速度!
在深入研究之前,让我们确保我们正在使用 GPU 进行此演示。
为此,请选择“运行时”->“更改运行时类型”->“硬件加速器”->“GPU”。
以下代码段将验证我们是否可以访问 GPU。
if tf.test.gpu_device_name() != '/device:GPU:0':
print('WARNING: GPU device not found.')
else:
print('SUCCESS: Found GPU: {}'.format(tf.test.gpu_device_name()))
WARNING: GPU device not found.
数据
我们使用来自流行的 lme4 R 包(Bates 等人,2015)的 InstEval 数据集。它是一个包含课程及其评估评分的数据集。每个课程都包含元数据,例如 学生、讲师 和 系别,我们感兴趣的响应变量是评估评分。
def load_insteval():
"""Loads the InstEval data set.
It contains 73,421 university lecture evaluations by students at ETH
Zurich with a total of 2,972 students, 2,160 professors and
lecturers, and several student, lecture, and lecturer attributes.
Implementation is built from the `observations` Python package.
Returns:
Tuple of np.ndarray `x_train` with 73,421 rows and 7 columns and
dictionary `metadata` of column headers (feature names).
"""
url = ('https://raw.github.com/vincentarelbundock/Rdatasets/master/csv/'
'lme4/InstEval.csv')
with requests.Session() as s:
download = s.get(url)
f = download.content.decode().splitlines()
iterator = csv.reader(f)
columns = next(iterator)[1:]
x_train = np.array([row[1:] for row in iterator], dtype=np.int)
metadata = {'columns': columns}
return x_train, metadata
我们加载并预处理数据集。我们保留了 20% 的数据,以便我们可以对未见过的数据点评估拟合的模型。下面我们可视化前几行。
data, metadata = load_insteval()
data = pd.DataFrame(data, columns=metadata['columns'])
data = data.rename(columns={'s': 'students',
'd': 'instructors',
'dept': 'departments',
'y': 'ratings'})
data['students'] -= 1 # start index by 0
# Remap categories to start from 0 and end at max(category).
data['instructors'] = data['instructors'].astype('category').cat.codes
data['departments'] = data['departments'].astype('category').cat.codes
train = data.sample(frac=0.8)
test = data.drop(train.index)
train.head()
<ipython-input-4-5d7a9eabeea1>:21: DeprecationWarning: `np.int` is a deprecated alias for the builtin `int`. To silence this warning, use `int` by itself. Doing this will not modify any behavior and is safe. When replacing `np.int`, you may wish to use e.g. `np.int64` or `np.int32` to specify the precision. If you wish to review your current use, check the release note link for additional information. Deprecated in NumPy 1.20; for more details and guidance: https://numpy.com.cn/devdocs/release/1.20.0-notes.html#deprecations x_train = np.array([row[1:] for row in iterator], dtype=np.int)
我们根据输入的 特征 字典和对应于评分的 标签 输出设置数据集。每个特征都编码为整数,每个标签(评估评分)都编码为浮点数。
get_value = lambda dataframe, key, dtype: dataframe[key].values.astype(dtype)
features_train = {
k: get_value(train, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_train = get_value(train, key='ratings', dtype=np.float32)
features_test = {k: get_value(test, key=k, dtype=np.int32)
for k in ['students', 'instructors', 'departments', 'service']}
labels_test = get_value(test, key='ratings', dtype=np.float32)
num_students = max(features_train['students']) + 1
num_instructors = max(features_train['instructors']) + 1
num_departments = max(features_train['departments']) + 1
num_observations = train.shape[0]
print("Number of students:", num_students)
print("Number of instructors:", num_instructors)
print("Number of departments:", num_departments)
print("Number of observations:", num_observations)
Number of students: 2972 Number of instructors: 1128 Number of departments: 14 Number of observations: 58737
模型
典型的线性模型假设独立性,其中任何一对数据点都具有恒定的线性关系。在 InstEval 数据集中,观察结果出现在组中,每个组可能具有不同的斜率和截距。线性混合效应模型(也称为分层线性模型或多级线性模型)捕获了这种现象(Gelman & Hill,2006)。
这种现象的例子包括
- 学生。来自学生的观察结果不是独立的:有些学生可能会系统地给出较低(或较高)的讲座评分。
- 讲师。来自讲师的观察结果不是独立的:我们预计优秀的教师通常会获得良好的评分,而糟糕的教师通常会获得糟糕的评分。
- 系别。来自系的观察结果不是独立的:某些系可能通常具有枯燥的材料或更严格的评分,因此评分低于其他系。
为了捕获这一点,回想一下,对于 \(N\times D\) 特征 \(\mathbf{X}\) 和 \(N\) 标签 \(\mathbf{y}\) 的数据集,线性回归假设模型
\[ \begin{equation*} \mathbf{y} = \mathbf{X}\beta + \alpha + \epsilon, \end{equation*} \]
其中存在斜率向量 \(\beta\in\mathbb{R}^D\)、截距 \(\alpha\in\mathbb{R}\) 和随机噪声 \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\)。我们说 \(\beta\) 和 \(\alpha\) 是“固定效应”:它们是跨数据点 \((x, y)\) 的总体保持不变的效应。该方程作为似然的等效公式是 \(\mathbf{y} \sim \text{Normal}(\mathbf{X}\beta + \alpha, \mathbf{I})\)。在推理过程中,此似然被最大化,以找到适合数据的 \(\beta\) 和 \(\alpha\) 的点估计。
线性混合效应模型将线性回归扩展为
\[ \begin{align*} \eta &\sim \text{Normal}(\mathbf{0}, \sigma^2 \mathbf{I}), \\ \mathbf{y} &= \mathbf{X}\beta + \mathbf{Z}\eta + \alpha + \epsilon. \end{align*} \]
其中仍然存在斜率向量 \(\beta\in\mathbb{R}^P\),截距 \(\alpha\in\mathbb{R}\),以及随机噪声 \(\epsilon\sim\text{Normal}(\mathbf{0}, \mathbf{I})\)。此外,还有一个项 \(\mathbf{Z}\eta\),其中 \(\mathbf{Z}\) 是特征矩阵,\(\eta\in\mathbb{R}^Q\) 是随机斜率向量;\(\eta\) 服从正态分布,方差分量参数为 \(\sigma^2\)。\(\mathbf{Z}\) 是通过将原始 \(N\times D\) 特征矩阵划分为新的 \(N\times P\) 矩阵 \(\mathbf{X}\) 和 \(N\times Q\) 矩阵 \(\mathbf{Z}\) 来形成的,其中 \(P + Q=D\):这种划分允许我们分别使用固定效应 \(\beta\) 和潜在变量 \(\eta\) 对特征进行建模。
我们说潜在变量 \(\eta\) 是“随机效应”:它们是跨人群变化的效应(尽管它们在亚人群中可能是恒定的)。特别是,由于随机效应 \(\eta\) 的均值为 0,数据标签的均值由 \(\mathbf{X}\beta + \alpha\) 捕获。随机效应分量 \(\mathbf{Z}\eta\) 捕获数据中的变化:例如,“讲师 #54 的评分比平均值高 1.4 分。”
在本教程中,我们假设以下效应
- 固定效应:
service。service是一个二元协变量,对应于课程是否属于讲师的主要部门。无论我们收集多少额外数据,它只能取值 \(0\) 和 \(1\)。 - 随机效应:
students,instructors,以及departments。如果从课程评估评分人群中获得更多观察结果,我们可能会看到新的学生、教师或部门。
在 R 的 lme4 包(Bates 等人,2015)的语法中,模型可以概括为
ratings ~ service + (1|students) + (1|instructors) + (1|departments) + 1
其中 x 表示固定效应,(1|x) 表示 x 的随机效应,1 表示截距项。
我们在下面将此模型实现为 JointDistribution。为了更好地支持参数跟踪(例如,我们希望跟踪 tf.Variable 中的所有 model.trainable_variables),我们将模型模板实现为 tf.Module。
class LinearMixedEffectModel(tf.Module):
def __init__(self):
# Set up fixed effects and other parameters.
# These are free parameters to be optimized in E-steps
self._intercept = tf.Variable(0., name="intercept") # alpha in eq
self._effect_service = tf.Variable(0., name="effect_service") # beta in eq
self._stddev_students = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_students") # sigma in eq
self._stddev_instructors = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_instructors") # sigma in eq
self._stddev_departments = tfp.util.TransformedVariable(
1., bijector=tfb.Exp(), name="stddev_departments") # sigma in eq
def __call__(self, features):
model = tfd.JointDistributionSequential([
# Set up random effects.
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_students),
scale_diag=self._stddev_students * tf.ones(num_students)),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_instructors),
scale_diag=self._stddev_instructors * tf.ones(num_instructors)),
tfd.MultivariateNormalDiag(
loc=tf.zeros(num_departments),
scale_diag=self._stddev_departments * tf.ones(num_departments)),
# This is the likelihood for the observed.
lambda effect_departments, effect_instructors, effect_students: tfd.Independent(
tfd.Normal(
loc=(self._effect_service * features["service"] +
tf.gather(effect_students, features["students"], axis=-1) +
tf.gather(effect_instructors, features["instructors"], axis=-1) +
tf.gather(effect_departments, features["departments"], axis=-1) +
self._intercept),
scale=1.),
reinterpreted_batch_ndims=1)
])
# To enable tracking of the trainable variables via the created distribution,
# we attach a reference to `self`. Since all TFP objects sub-class
# `tf.Module`, this means that the following is possible:
# LinearMixedEffectModel()(features_train).trainable_variables
# ==> tuple of all tf.Variables created by LinearMixedEffectModel.
model._to_track = self
return model
lmm_jointdist = LinearMixedEffectModel()
# Conditioned on feature/predictors from the training data
lmm_train = lmm_jointdist(features_train)
lmm_train.trainable_variables
(<tf.Variable 'effect_service:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'intercept:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_departments:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_instructors:0' shape=() dtype=float32, numpy=0.0>, <tf.Variable 'stddev_students:0' shape=() dtype=float32, numpy=0.0>)
作为一个概率图程序,我们也可以根据其计算图来可视化模型的结构。该图编码了程序中随机变量之间的dataflow,明确地表示了它们在图形模型(Jordan,2003)中的关系。
作为一个统计工具,我们可能会查看该图,以便更好地看到,例如,intercept 和 effect_service 在给定 ratings 的情况下是条件相关的;如果程序是用类、跨模块的交叉引用和/或子例程编写的,这可能难以从源代码中看到。作为一个计算工具,我们也可能会注意到潜在变量通过 tf.gather 操作流入 ratings 变量。如果索引 Tensor 很昂贵,这可能是某些硬件加速器的瓶颈;可视化图形使这一点一目了然。
lmm_train.resolve_graph()
(('effect_students', ()),
('effect_instructors', ()),
('effect_departments', ()),
('x', ('effect_departments', 'effect_instructors', 'effect_students')))
参数估计
给定数据,推理的目标是拟合模型的固定效应斜率 \(\beta\),截距 \(\alpha\) 和方差分量参数 \(\sigma^2\)。最大似然原理将此任务形式化为
\[ \max_{\beta, \alpha, \sigma}~\log p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}; \beta, \alpha, \sigma) = \max_{\beta, \alpha, \sigma}~\log \int p(\eta; \sigma) ~p(\mathbf{y}\mid \mathbf{X}, \mathbf{Z}, \eta; \beta, \alpha)~d\eta. \]
在本教程中,我们使用蒙特卡罗 EM 算法来最大化此边际密度(Dempster 等人,1977;Wei 和 Tanner,1990)。¹ 我们执行马尔可夫链蒙特卡罗来计算条件似然的期望,相对于随机效应(“E 步”),然后我们执行梯度下降来最大化期望,相对于参数(“M 步”)。
对于 E 步,我们设置了哈密顿蒙特卡罗 (HMC)。它接受当前状态——学生、讲师和部门效应——并返回一个新状态。我们将新状态分配给 TensorFlow 变量,这些变量将表示 HMC 链的状态。
对于 M 步,我们使用来自 HMC 的后验样本来计算边际似然的无偏估计,直到一个常数。然后,我们应用其相对于感兴趣参数的梯度。这会在边际似然上产生一个无偏随机下降步骤。我们使用 Adam TensorFlow 优化器实现它,并最小化边际的负值。
target_log_prob_fn = lambda *x: lmm_train.log_prob(x + (labels_train,))
trainable_variables = lmm_train.trainable_variables
current_state = lmm_train.sample()[:-1]
# For debugging
target_log_prob_fn(*current_state)
<tf.Tensor: shape=(), dtype=float32, numpy=-485996.53>
# Set up E-step (MCMC).
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
step_size=0.015,
num_leapfrog_steps=3)
kernel_results = hmc.bootstrap_results(current_state)
@tf.function(autograph=False, jit_compile=True)
def one_e_step(current_state, kernel_results):
next_state, next_kernel_results = hmc.one_step(
current_state=current_state,
previous_kernel_results=kernel_results)
return next_state, next_kernel_results
optimizer = tf_keras.optimizers.Adam(learning_rate=.01)
# Set up M-step (gradient descent).
@tf.function(autograph=False, jit_compile=True)
def one_m_step(current_state):
with tf.GradientTape() as tape:
loss = -target_log_prob_fn(*current_state)
grads = tape.gradient(loss, trainable_variables)
optimizer.apply_gradients(zip(grads, trainable_variables))
return loss
我们执行一个预热阶段,该阶段运行一个 MCMC 链进行一定次数的迭代,以便训练可以在后验的概率质量内初始化。然后我们运行一个训练循环。它联合运行 E 步和 M 步,并在训练期间记录值。
num_warmup_iters = 1000
num_iters = 1500
num_accepted = 0
effect_students_samples = np.zeros([num_iters, num_students])
effect_instructors_samples = np.zeros([num_iters, num_instructors])
effect_departments_samples = np.zeros([num_iters, num_departments])
loss_history = np.zeros([num_iters])
# Run warm-up stage.
for t in range(num_warmup_iters):
current_state, kernel_results = one_e_step(current_state, kernel_results)
num_accepted += kernel_results.is_accepted.numpy()
if t % 500 == 0 or t == num_warmup_iters - 1:
print("Warm-Up Iteration: {:>3} Acceptance Rate: {:.3f}".format(
t, num_accepted / (t + 1)))
num_accepted = 0 # reset acceptance rate counter
# Run training.
for t in range(num_iters):
# run 5 MCMC iterations before every joint EM update
for _ in range(5):
current_state, kernel_results = one_e_step(current_state, kernel_results)
loss = one_m_step(current_state)
effect_students_samples[t, :] = current_state[0].numpy()
effect_instructors_samples[t, :] = current_state[1].numpy()
effect_departments_samples[t, :] = current_state[2].numpy()
num_accepted += kernel_results.is_accepted.numpy()
loss_history[t] = loss.numpy()
if t % 500 == 0 or t == num_iters - 1:
print("Iteration: {:>4} Acceptance Rate: {:.3f} Loss: {:.3f}".format(
t, num_accepted / (t + 1), loss_history[t]))
Warm-Up Iteration: 0 Acceptance Rate: 1.000 Warm-Up Iteration: 500 Acceptance Rate: 0.758 Warm-Up Iteration: 999 Acceptance Rate: 0.729 Iteration: 0 Acceptance Rate: 1.000 Loss: 98200.422 Iteration: 500 Acceptance Rate: 0.649 Loss: 98190.469 Iteration: 1000 Acceptance Rate: 0.656 Loss: 98068.664 Iteration: 1499 Acceptance Rate: 0.663 Loss: 98155.070
您还可以将预热 for 循环写入 tf.while_loop,并将训练步骤写入 tf.scan 或 tf.while_loop,以实现更快的推理。例如
@tf.function(autograph=False, jit_compile=True)
def run_k_e_steps(k, current_state, kernel_results):
_, next_state, next_kernel_results = tf.while_loop(
cond=lambda i, state, pkr: i < k,
body=lambda i, state, pkr: (i+1, *one_e_step(state, pkr)),
loop_vars=(tf.constant(0), current_state, kernel_results)
)
return next_state, next_kernel_results
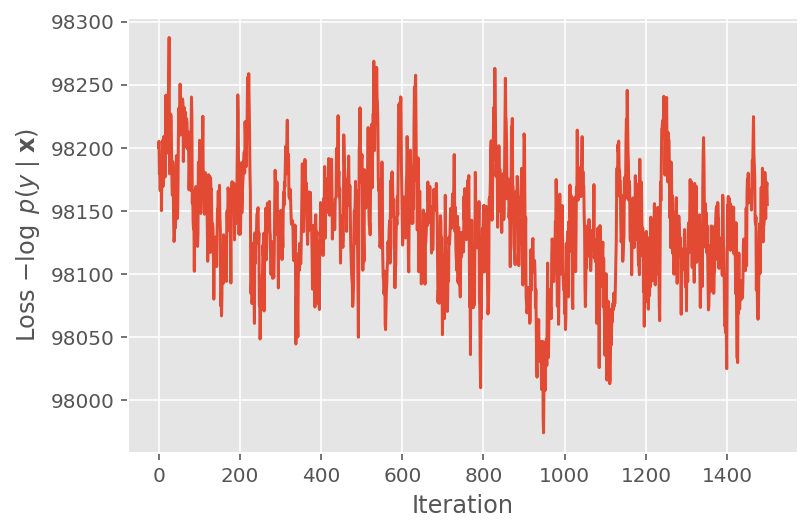
在上面,我们没有运行算法,直到检测到收敛阈值。为了检查训练是否合理,我们验证损失函数确实在训练迭代中趋于收敛。
plt.plot(loss_history)
plt.ylabel(r'Loss $-\log$ $p(y\mid\mathbf{x})$')
plt.xlabel('Iteration')
plt.show()
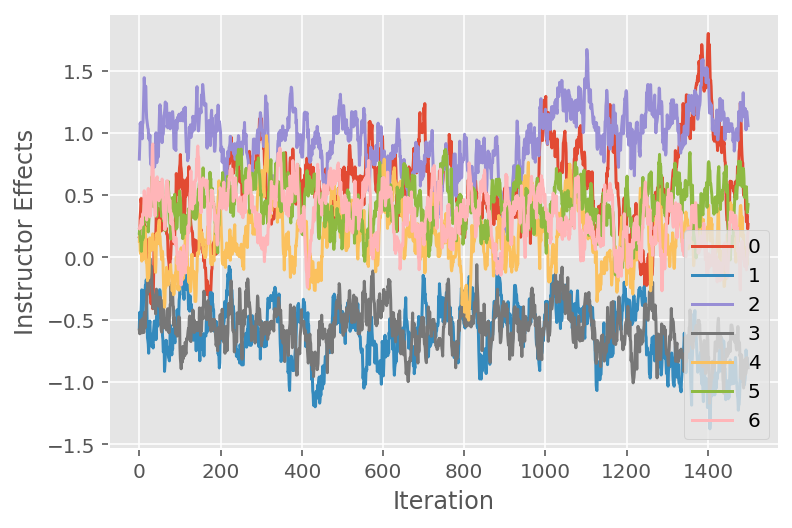
我们还使用轨迹图,它显示了马尔可夫链蒙特卡罗算法在特定潜在维度上的轨迹。下面我们看到,特定讲师效应确实有意义地从其初始状态过渡,并探索状态空间。轨迹图还表明,效应在不同的讲师之间有所不同,但具有相似的混合行为。
for i in range(7):
plt.plot(effect_instructors_samples[:, i])
plt.legend([i for i in range(7)], loc='lower right')
plt.ylabel('Instructor Effects')
plt.xlabel('Iteration')
plt.show()
批评
在上面,我们拟合了模型。我们现在开始使用数据来批评它的拟合,这让我们可以探索和更好地理解模型。一种这样的技术是残差图,它绘制了模型预测与每个数据点的真实值之间的差异。如果模型是正确的,那么它们的差异应该服从标准正态分布;图中任何偏离这种模式的现象都表明模型拟合不佳。
我们通过首先形成评分的后验预测分布来构建残差图,该分布用给定训练数据的随机效应的后验替换了随机效应的先验分布。特别是,我们向前运行模型,并用其推断的后验均值截取其对先验随机效应的依赖。²
lmm_test = lmm_jointdist(features_test)
[
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
] = [
np.mean(x, axis=0).astype(np.float32) for x in [
effect_students_samples,
effect_instructors_samples,
effect_departments_samples
]
]
# Get the posterior predictive distribution
(*posterior_conditionals, ratings_posterior), _ = lmm_test.sample_distributions(
value=(
effect_students_mean,
effect_instructors_mean,
effect_departments_mean,
))
ratings_prediction = ratings_posterior.mean()
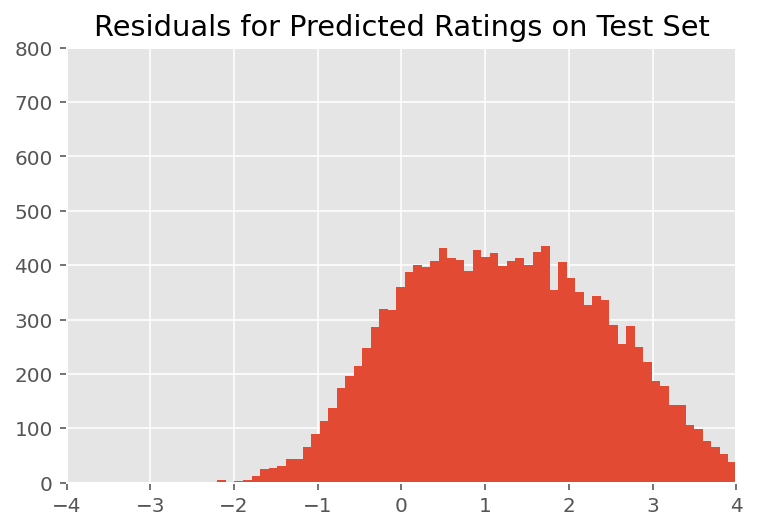
经过目视检查,残差看起来有点像标准正态分布。但是,拟合并不完美:尾部中的概率质量比正态分布更大,这表明模型可以通过放宽其正态性假设来改进其拟合。
特别是,虽然在 InstEval 数据集中使用正态分布来模拟评分是最常见的,但仔细观察数据会发现,课程评估评分实际上是 1 到 5 的序数值。这表明我们应该使用序数分布,或者如果我们有足够的数据来丢弃相对排序,甚至可以使用分类分布。这只是对上面模型的一行更改;相同的推理代码适用。
plt.title("Residuals for Predicted Ratings on Test Set")
plt.xlim(-4, 4)
plt.ylim(0, 800)
plt.hist(ratings_prediction - labels_test, 75)
plt.show()
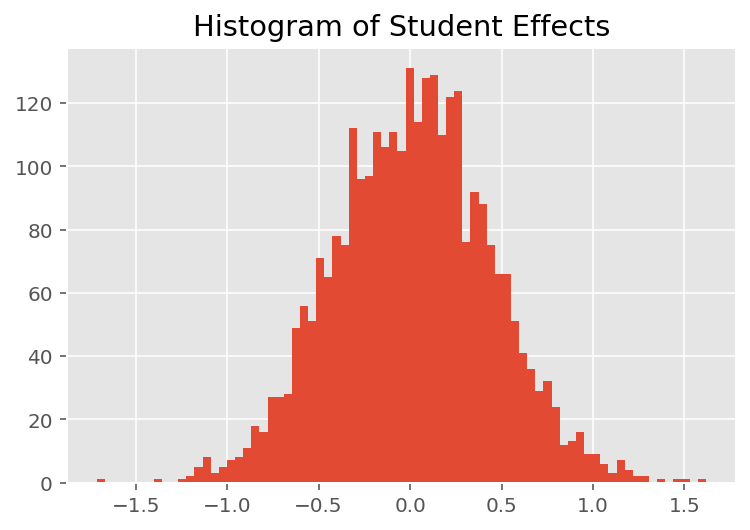
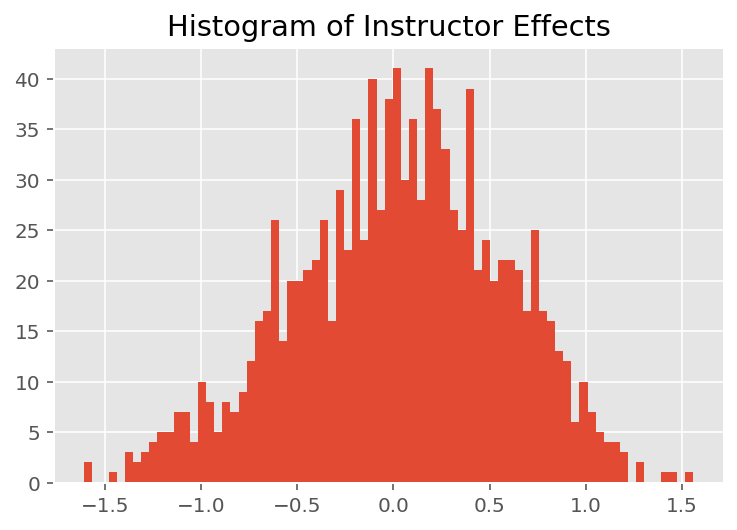
为了探索模型如何进行单个预测,我们查看了学生、讲师和部门效应的直方图。这让我们了解数据点特征向量中的单个元素如何倾向于影响结果。
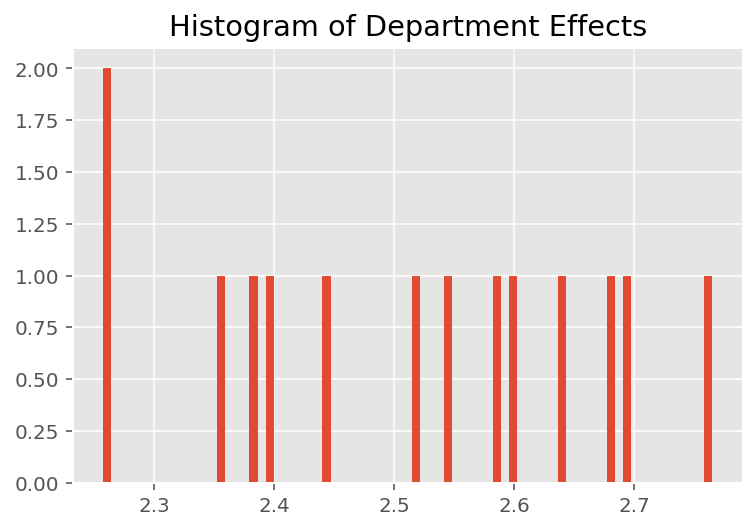
不出所料,我们看到下面每个学生通常对讲师的评估评分影响很小。有趣的是,我们看到讲师所属的部门有很大的影响。
plt.title("Histogram of Student Effects")
plt.hist(effect_students_mean, 75)
plt.show()
plt.title("Histogram of Instructor Effects")
plt.hist(effect_instructors_mean, 75)
plt.show()
plt.title("Histogram of Department Effects")
plt.hist(effect_departments_mean, 75)
plt.show()
脚注
¹ 线性混合效应模型是一个特殊情况,我们可以分析地计算其边际密度。在本教程中,我们演示了蒙特卡罗 EM,它更容易应用于非分析边际密度,例如,如果似然扩展为分类而不是正态。
² 为简单起见,我们使用模型的一次前向传递来形成预测分布的均值。这是通过对后验均值进行条件化来完成的,对于线性混合效应模型是有效的。但是,这在一般情况下是无效的:后验预测分布的均值通常是难以处理的,需要在给定后验样本的情况下,对模型的多个前向传递进行经验均值。
致谢
本教程最初是在 Edward 1.0 中编写的 (源代码)。我们感谢所有为编写和修改该版本做出贡献的人。
参考文献
Douglas Bates 和 Martin Machler 和 Ben Bolker 和 Steve Walker。使用 lme4 拟合线性混合效应模型。统计软件杂志,67(1):1-48,2015。
Arthur P. Dempster、Nan M. Laird 和 Donald B. Rubin。通过 EM 算法从不完整数据中获得最大似然。皇家统计学会杂志,B 系列(方法论),1-38,1977。
Andrew Gelman 和 Jennifer Hill。使用回归和多级/分层模型进行数据分析。剑桥大学出版社,2006。
David A. Harville。方差分量估计和相关问题的最大似然方法。美国统计协会杂志,72(358):320-338,1977。
Michael I. Jordan。图形模型简介。技术报告,2003。
Nan M. Laird 和 James Ware。纵向数据的随机效应模型。生物统计学,963-974,1982。
Greg Wei 和 Martin A. Tanner。EM 算法的蒙特卡罗实现和穷人的数据增强算法。美国统计协会杂志,699-704,1990。
