在 TensorFlow.org 上查看

在 Google Colab 中运行

在 GitHub 上查看源代码

下载笔记本

import numpy as np
import matplotlib.pyplot as plt
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()

import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors

一个 [copula](https://en.wikipedia.org/wiki/Copula_(probability_theory%29) 是捕获随机变量之间依赖关系的经典方法。更正式地说，copula 是一个多元分布 \(C(U_1, U_2, ...., U_n)\)，使得边缘化得到 \(U_i \sim \text{Uniform}(0, 1)\)。

Copulas 很有趣，因为我们可以使用它们来创建具有任意边缘的 multivariate 分布。这是食谱

• 使用 概率积分变换 将任意连续 R.V. \(X\) 转换为均匀的 \(F_X(X)\)，其中 \(F_X\) 是 \(X\) 的 CDF。
• 给定一个 copula（例如双变量）\(C(U, V)\)，我们有 \(U\) 和 \(V\) 具有均匀边缘分布。
• 现在给定我们感兴趣的 R.V. \(X, Y\)，创建一个新的分布 \(C'(X, Y) = C(F_X(X), F_Y(Y))\)。\(X\) 和 \(Y\) 的边缘是我们想要的。

边缘是单变量的，因此可能更容易测量和/或建模。copula 使得能够从边缘开始，但也能实现维度之间的任意相关性。

高斯 Copula

为了说明 copulas 是如何构建的，请考虑根据多元高斯相关性捕获依赖关系的情况。高斯 Copula 是由 \(C(u_1, u_2, ...u_n) = \Phi_\Sigma(\Phi^{-1}(u_1), \Phi^{-1}(u_2), ... \Phi^{-1}(u_n))\) 给出的，其中 \(\Phi_\Sigma\) 表示多元正态的 CDF，协方差为 \(\Sigma\)，均值为 0，\(\Phi^{-1}\) 是标准正态的逆 CDF。

应用正态的逆 CDF 会扭曲均匀维度使其呈正态分布。然后应用多元正态的 CDF 会压缩分布使其边缘均匀，并具有高斯相关性。

因此，我们得到的是高斯 Copula 是一个在单位超立方体 \([0, 1]^n\) 上的分布，具有均匀边缘。

如此定义，高斯 Copula 可以使用 tfd.TransformedDistribution 和适当的 Bijector 实现。也就是说，我们正在通过使用正态分布的逆 CDF（由 tfb.NormalCDF 双射器实现）来转换多元正态。

下面，我们实现了一个高斯 Copula，并做了一个简化假设：协方差由 Cholesky 因子参数化（因此是 MultivariateNormalTriL 的协方差）。（可以使用其他 tf.linalg.LinearOperators 来编码不同的无矩阵假设）。

class GaussianCopulaTriL(tfd.TransformedDistribution):
  """Takes a location, and lower triangular matrix for the Cholesky factor."""
  def __init__(self, loc, scale_tril):
    super(GaussianCopulaTriL, self).__init__(
        distribution=tfd.MultivariateNormalTriL(
            loc=loc,
            scale_tril=scale_tril),
        bijector=tfb.NormalCDF(),
        validate_args=False,
        name="GaussianCopulaTriLUniform")


# Plot an example of this.
unit_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(unit_interval, unit_interval)
coordinates = np.concatenate(
    [x_grid[..., np.newaxis],
     y_grid[..., np.newaxis]], axis=-1)

pdf = GaussianCopulaTriL(
    loc=[0., 0.],
    scale_tril=[[1., 0.8], [0., 0.6]],
).prob(coordinates)

# Plot its density.

plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);

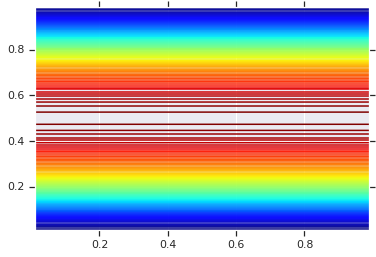
然而，这种模型的强大之处在于使用概率积分变换，将 copula 应用于任意 R.V.s。这样，我们可以指定任意边缘，并使用 copula 将它们缝合在一起。

我们从一个模型开始

\[\begin{align*} X &\sim \text{Kumaraswamy}(a, b) \\ Y &\sim \text{Gumbel}(\mu, \beta) \end{align*}\]

并使用 copula 获取一个双变量 R.V. \(Z\)，它具有 Kumaraswamy 和 Gumbel 边缘。

我们将首先绘制由这两个 R.V.s 生成的乘积分布。这只是为了作为我们应用 Copula 时的比较点。

a = 2.0
b = 2.0
gloc = 0.
gscale = 1.

x = tfd.Kumaraswamy(a, b)
y = tfd.Gumbel(loc=gloc, scale=gscale)

# Plot the distributions, assuming independence
x_axis_interval = np.linspace(0.01, 0.99, num=200, dtype=np.float32)
y_axis_interval = np.linspace(-2., 3., num=200, dtype=np.float32)
x_grid, y_grid = np.meshgrid(x_axis_interval, y_axis_interval)

pdf = x.prob(x_grid) * y.prob(y_grid)

# Plot its density

plt.contour(x_grid, y_grid, pdf, 100, cmap=plt.cm.jet);

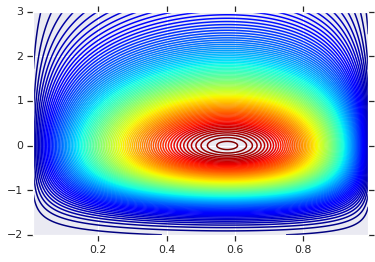
具有不同边缘的联合分布

现在我们使用高斯 copula 将分布耦合在一起，并绘制出来。同样，我们选择使用 TransformedDistribution 应用适当的 Bijector 来获得所选边缘。

具体来说，我们使用了一个 Blockwise 双射器，它在向量的不同部分应用不同的双射器（这仍然是一个双射变换）。

现在我们可以定义我们想要的 Copula。给定一个目标边缘分布的列表（以双射器形式编码），我们可以轻松地构建一个使用 Copula 并具有指定边缘分布的新分布。

class WarpedGaussianCopula(tfd.TransformedDistribution):
  """Application of a Gaussian Copula on a list of target marginals.

  This implements an application of a Gaussian Copula. Given [x_0, ... x_n]
  which are distributed marginally (with CDF) [F_0, ... F_n],
  `GaussianCopula` represents an application of the Copula, such that the
  resulting multivariate distribution has the above specified marginals.

  The marginals are specified by `marginal_bijectors`: These are
  bijectors whose `inverse` encodes the CDF and `forward` the inverse CDF.

  block_sizes is a 1-D Tensor to determine splits for `marginal_bijectors`
  length should be same as length of `marginal_bijectors`.
  See tfb.Blockwise for details
  """
  def __init__(self, loc, scale_tril, marginal_bijectors, block_sizes=None):
    super(WarpedGaussianCopula, self).__init__(
        distribution=GaussianCopulaTriL(loc=loc, scale_tril=scale_tril),
        bijector=tfb.Blockwise(bijectors=marginal_bijectors,
                               block_sizes=block_sizes),
        validate_args=False,
        name="GaussianCopula")

最后，让我们实际使用这个高斯 Copula。我们将使用 \(\begin{bmatrix}1 & 0\\\rho & \sqrt{(1-\rho^2)}\end{bmatrix}\) 的 Cholesky 分解，它将对应于方差为 1，多元正态分布的相关性为 \(\rho\)。

我们将查看一些情况。

# Create our coordinates:
coordinates = np.concatenate(
    [x_grid[..., np.newaxis], y_grid[..., np.newaxis]], -1)


def create_gaussian_copula(correlation):
  # Use Gaussian Copula to add dependence.
  return WarpedGaussianCopula(
      loc=[0.,  0.],
      scale_tril=[[1., 0.], [correlation, tf.sqrt(1. - correlation ** 2)]],
      # These encode the marginals we want. In this case we want X_0 has
      # Kumaraswamy marginal, and X_1 has Gumbel marginal.

      marginal_bijectors=[
          tfb.Invert(tfb.KumaraswamyCDF(a, b)),
          tfb.Invert(tfb.GumbelCDF(loc=0., scale=1.))])


# Note that the zero case will correspond to independent marginals!
correlations = [0., -0.8, 0.8]
copulas = []
probs = []
for correlation in correlations:
  copula = create_gaussian_copula(correlation)
  copulas.append(copula)
  probs.append(copula.prob(coordinates))


# Plot it's density

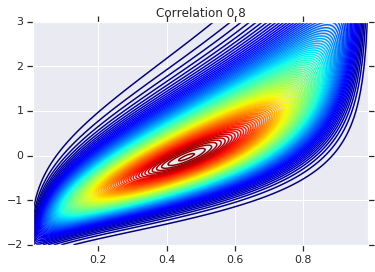
for correlation, copula_prob in zip(correlations, probs):
  plt.figure()
  plt.contour(x_grid, y_grid, copula_prob, 100, cmap=plt.cm.jet)
  plt.title('Correlation {}'.format(correlation))

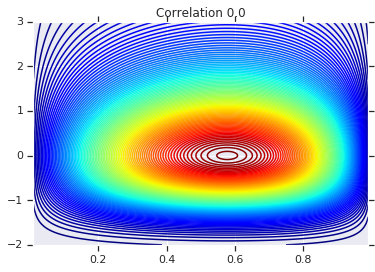
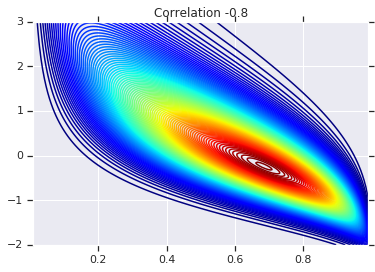
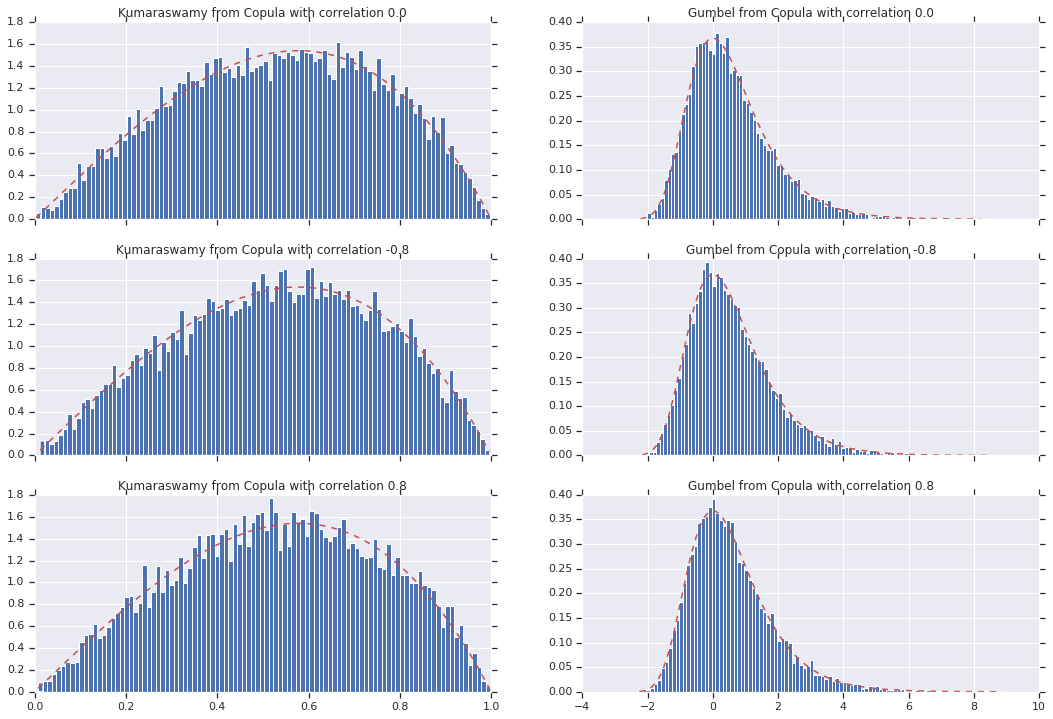
最后，让我们验证我们是否真正得到了我们想要的边缘分布。

def kumaraswamy_pdf(x):
    return tfd.Kumaraswamy(a, b).prob(np.float32(x))

def gumbel_pdf(x):
    return tfd.Gumbel(gloc, gscale).prob(np.float32(x))


copula_samples = []
for copula in copulas:
  copula_samples.append(copula.sample(10000))

plot_rows = len(correlations)
plot_cols = 2  # for 2  densities [kumarswamy, gumbel]
fig, axes = plt.subplots(plot_rows, plot_cols, sharex='col', figsize=(18,12))

# Let's marginalize out on each, and plot the samples.

for i, (correlation, copula_sample) in enumerate(zip(correlations, copula_samples)):
  k = copula_sample[..., 0].numpy()
  g = copula_sample[..., 1].numpy()


  _, bins, _ = axes[i, 0].hist(k, bins=100, density=True)
  axes[i, 0].plot(bins, kumaraswamy_pdf(bins), 'r--')
  axes[i, 0].set_title('Kumaraswamy from Copula with correlation {}'.format(correlation))

  _, bins, _ = axes[i, 1].hist(g, bins=100, density=True)
  axes[i, 1].plot(bins, gumbel_pdf(bins), 'r--')
  axes[i, 1].set_title('Gumbel from Copula with correlation {}'.format(correlation))

结论

就这样！我们已经证明了我们可以使用 Bijector API 构建高斯 Copula。

更一般地说，使用 Bijector API 编写双射器，并将它们与分布组合起来，可以创建丰富的分布族，用于灵活的建模。