 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
在这个 Colab 中,我们将探索仅使用 TensorFlow Probability 原语从贝叶斯高斯混合模型 (BGMM) 后验中采样。
模型
对于 \(k\in\{1,\ldots, K\}\) 个混合分量,每个分量都是 \(D\) 维的,我们希望使用以下贝叶斯高斯混合模型对 \(i\in\{1,\ldots,N\}\) 个 iid 样本进行建模
\[\begin{align*} \theta &\sim \text{Dirichlet}(\text{concentration}=\alpha_0)\\ \mu_k &\sim \text{Normal}(\text{loc}=\mu_{0k}, \text{scale}=I_D)\\ T_k &\sim \text{Wishart}(\text{df}=5, \text{scale}=I_D)\\ Z_i &\sim \text{Categorical}(\text{probs}=\theta)\\ Y_i &\sim \text{Normal}(\text{loc}=\mu_{z_i}, \text{scale}=T_{z_i}^{-1/2})\\ \end{align*}\]
注意,scale 参数都具有 cholesky 语义。我们使用此约定,因为它是 TF Distributions 的约定(它本身部分使用此约定,因为它在计算上有利)。
我们的目标是从后验生成样本
\[p\left(\theta, \{\mu_k, T_k\}_{k=1}^K \Big| \{y_i\}_{i=1}^N, \alpha_0, \{\mu_{ok}\}_{k=1}^K\right)\]
请注意,\(\{Z_i\}_{i=1}^N\) 不存在 - 我们只对那些不随 \(N\) 缩放的随机变量感兴趣。(幸运的是,有一个 TF 分布可以处理对 \(Z_i\) 进行边缘化。)
由于计算上难以处理的归一化项,因此无法直接从该分布中采样。
Metropolis-Hastings 算法 是从难以归一化的分布中采样的技术。
TensorFlow Probability 提供了许多 MCMC 选项,包括几个基于 Metropolis-Hastings 的选项。在本笔记本中,我们将使用 哈密顿蒙特卡罗 (tfp.mcmc.HamiltonianMonteCarlo)。HMC 通常是一个不错的选择,因为它可以快速收敛,联合采样状态空间(而不是逐坐标采样),并利用 TF 的优势之一:自动微分。也就是说,从 BGMM 后验中采样实际上可能更适合使用其他方法,例如 吉布斯采样。
%matplotlib inline
import functools
import matplotlib.pyplot as plt; plt.style.use('ggplot')
import numpy as np
import seaborn as sns; sns.set_context('notebook')
import tensorflow.compat.v2 as tf
tf.enable_v2_behavior()
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.bijectors
physical_devices = tf.config.experimental.list_physical_devices('GPU')
if len(physical_devices) > 0:
tf.config.experimental.set_memory_growth(physical_devices[0], True)
在实际构建模型之前,我们需要定义一种新的分布类型。从上面的模型规范可以清楚地看出,我们使用逆协方差矩阵,即 [精度矩阵](https://en.wikipedia.org/wiki/Precision_(statistics%29) 来参数化 MVN。为了在 TF 中实现这一点,我们需要推出我们的 Bijector。此 Bijector 将使用以下正向变换
Y = tf.linalg.triangular_solve((tf.linalg.matrix_transpose(chol_precision_tril), X, adjoint=True) + loc.
而 log_prob 计算只是反向,即
X = tf.linalg.matmul(chol_precision_tril, X - loc, adjoint_a=True).
由于我们只需要 log_prob,这意味着我们永远不会调用 tf.linalg.triangular_solve(就像 tfd.MultivariateNormalTriL 的情况一样)。这是有利的,因为 tf.linalg.matmul 通常由于更好的缓存局部性而更快。
class MVNCholPrecisionTriL(tfd.TransformedDistribution):
"""MVN from loc and (Cholesky) precision matrix."""
def __init__(self, loc, chol_precision_tril, name=None):
super(MVNCholPrecisionTriL, self).__init__(
distribution=tfd.Independent(tfd.Normal(tf.zeros_like(loc),
scale=tf.ones_like(loc)),
reinterpreted_batch_ndims=1),
bijector=tfb.Chain([
tfb.Shift(shift=loc),
tfb.Invert(tfb.ScaleMatvecTriL(scale_tril=chol_precision_tril,
adjoint=True)),
]),
name=name)
tfd.Independent 分布将一个分布的独立抽取转换为具有统计独立坐标的多元分布。在计算 log_prob 方面,这种“元分布”表现为对事件维度(s)的简单求和。
还要注意,我们对比例矩阵取了 adjoint(“转置”)。这是因为如果精度是逆协方差,即 \(P=C^{-1}\) 并且如果 \(C=AA^\top\),则 \(P=BB^{\top}\),其中 \(B=A^{-\top}\)。
由于这种分布有点棘手,让我们快速验证一下我们的 MVNCholPrecisionTriL 是否按我们预期的那样工作。
def compute_sample_stats(d, seed=42, n=int(1e6)):
x = d.sample(n, seed=seed)
sample_mean = tf.reduce_mean(x, axis=0, keepdims=True)
s = x - sample_mean
sample_cov = tf.linalg.matmul(s, s, adjoint_a=True) / tf.cast(n, s.dtype)
sample_scale = tf.linalg.cholesky(sample_cov)
sample_mean = sample_mean[0]
return [
sample_mean,
sample_cov,
sample_scale,
]
dtype = np.float32
true_loc = np.array([1., -1.], dtype=dtype)
true_chol_precision = np.array([[1., 0.],
[2., 8.]],
dtype=dtype)
true_precision = np.matmul(true_chol_precision, true_chol_precision.T)
true_cov = np.linalg.inv(true_precision)
d = MVNCholPrecisionTriL(
loc=true_loc,
chol_precision_tril=true_chol_precision)
[sample_mean, sample_cov, sample_scale] = [
t.numpy() for t in compute_sample_stats(d)]
print('true mean:', true_loc)
print('sample mean:', sample_mean)
print('true cov:\n', true_cov)
print('sample cov:\n', sample_cov)
true mean: [ 1. -1.] sample mean: [ 1.0002806 -1.000105 ] true cov: [[ 1.0625 -0.03125 ] [-0.03125 0.015625]] sample cov: [[ 1.0641273 -0.03126175] [-0.03126175 0.01559312]]
由于样本均值和协方差接近真实均值和协方差,因此该分布似乎已正确实现。现在,我们将使用 MVNCholPrecisionTriL tfp.distributions.JointDistributionNamed 来指定 BGMM 模型。对于观测模型,我们将使用 tfd.MixtureSameFamily 来自动积分出 \(\{Z_i\}_{i=1}^N\) 抽取。
dtype = np.float64
dims = 2
components = 3
num_samples = 1000
bgmm = tfd.JointDistributionNamed(dict(
mix_probs=tfd.Dirichlet(
concentration=np.ones(components, dtype) / 10.),
loc=tfd.Independent(
tfd.Normal(
loc=np.stack([
-np.ones(dims, dtype),
np.zeros(dims, dtype),
np.ones(dims, dtype),
]),
scale=tf.ones([components, dims], dtype)),
reinterpreted_batch_ndims=2),
precision=tfd.Independent(
tfd.WishartTriL(
df=5,
scale_tril=np.stack([np.eye(dims, dtype=dtype)]*components),
input_output_cholesky=True),
reinterpreted_batch_ndims=1),
s=lambda mix_probs, loc, precision: tfd.Sample(tfd.MixtureSameFamily(
mixture_distribution=tfd.Categorical(probs=mix_probs),
components_distribution=MVNCholPrecisionTriL(
loc=loc,
chol_precision_tril=precision)),
sample_shape=num_samples)
))
def joint_log_prob(observations, mix_probs, loc, chol_precision):
"""BGMM with priors: loc=Normal, precision=Inverse-Wishart, mix=Dirichlet.
Args:
observations: `[n, d]`-shaped `Tensor` representing Bayesian Gaussian
Mixture model draws. Each sample is a length-`d` vector.
mix_probs: `[K]`-shaped `Tensor` representing random draw from
`Dirichlet` prior.
loc: `[K, d]`-shaped `Tensor` representing the location parameter of the
`K` components.
chol_precision: `[K, d, d]`-shaped `Tensor` representing `K` lower
triangular `cholesky(Precision)` matrices, each being sampled from
a Wishart distribution.
Returns:
log_prob: `Tensor` representing joint log-density over all inputs.
"""
return bgmm.log_prob(
mix_probs=mix_probs, loc=loc, precision=chol_precision, s=observations)
生成“训练”数据
在本演示中,我们将采样一些随机数据。
true_loc = np.array([[-2., -2],
[0, 0],
[2, 2]], dtype)
random = np.random.RandomState(seed=43)
true_hidden_component = random.randint(0, components, num_samples)
observations = (true_loc[true_hidden_component] +
random.randn(num_samples, dims).astype(dtype))
使用 HMC 进行贝叶斯推断
现在我们已经使用 TFD 指定了我们的模型并获得了一些观察数据,我们拥有运行 HMC 所需的所有必要部分。
为此,我们将使用 部分应用 来“固定”我们不想采样的内容。在这种情况下,这意味着我们只需要固定 observations。(超参数已烘焙到先验分布中,并且不是 joint_log_prob 函数签名的部分。)
unnormalized_posterior_log_prob = functools.partial(joint_log_prob, observations)
initial_state = [
tf.fill([components],
value=np.array(1. / components, dtype),
name='mix_probs'),
tf.constant(np.array([[-2., -2],
[0, 0],
[2, 2]], dtype),
name='loc'),
tf.linalg.eye(dims, batch_shape=[components], dtype=dtype, name='chol_precision'),
]
无约束表示
哈密顿蒙特卡罗 (HMC) 要求目标对数概率函数对其参数可微。此外,如果状态空间不受约束,HMC 可以表现出显著更高的统计效率。
这意味着在从 BGMM 后验中采样时,我们将需要解决两个主要问题
- \(\theta\) 表示一个离散概率向量,即必须满足 \(\sum_{k=1}^K \theta_k = 1\) 且 \(\theta_k>0\)。
- \(T_k\) 表示一个逆协方差矩阵,即必须满足 \(T_k \succ 0\),即为 正定。
为了满足此要求,我们需要
- 将受约束变量转换为无约束空间
- 在无约束空间中运行 MCMC
- 将无约束变量转换回受约束空间。
与 MVNCholPrecisionTriL 一样,我们将使用 Bijectors 将随机变量转换为无约束空间。
通过 softmax 函数 将
Dirichlet转换为无约束空间。我们的精度随机变量是正半定矩阵上的分布。为了取消约束这些矩阵,我们将使用
FillTriangular和TransformDiagonal双射。这些将向量转换为下三角矩阵,并确保对角线为正。前者很有用,因为它允许仅采样 \(d(d+1)/2\) 个浮点数,而不是 \(d^2\) 个。
unconstraining_bijectors = [
tfb.SoftmaxCentered(),
tfb.Identity(),
tfb.Chain([
tfb.TransformDiagonal(tfb.Softplus()),
tfb.FillTriangular(),
])]
@tf.function(autograph=False)
def sample():
return tfp.mcmc.sample_chain(
num_results=2000,
num_burnin_steps=500,
current_state=initial_state,
kernel=tfp.mcmc.SimpleStepSizeAdaptation(
tfp.mcmc.TransformedTransitionKernel(
inner_kernel=tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=unnormalized_posterior_log_prob,
step_size=0.065,
num_leapfrog_steps=5),
bijector=unconstraining_bijectors),
num_adaptation_steps=400),
trace_fn=lambda _, pkr: pkr.inner_results.inner_results.is_accepted)
[mix_probs, loc, chol_precision], is_accepted = sample()
现在我们将执行链并打印后验均值。
acceptance_rate = tf.reduce_mean(tf.cast(is_accepted, dtype=tf.float32)).numpy()
mean_mix_probs = tf.reduce_mean(mix_probs, axis=0).numpy()
mean_loc = tf.reduce_mean(loc, axis=0).numpy()
mean_chol_precision = tf.reduce_mean(chol_precision, axis=0).numpy()
precision = tf.linalg.matmul(chol_precision, chol_precision, transpose_b=True)
print('acceptance_rate:', acceptance_rate)
print('avg mix probs:', mean_mix_probs)
print('avg loc:\n', mean_loc)
print('avg chol(precision):\n', mean_chol_precision)
acceptance_rate: 0.5305 avg mix probs: [0.25248723 0.60729516 0.1402176 ] avg loc: [[-1.96466753 -2.12047249] [ 0.27628865 0.22944732] [ 2.06461244 2.54216122]] avg chol(precision): [[[ 1.05105032 0. ] [ 0.12699955 1.06553113]] [[ 0.76058015 0. ] [-0.50332767 0.77947431]] [[ 1.22770457 0. ] [ 0.70670027 1.50914164]]]
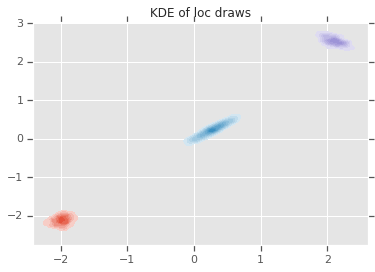
loc_ = loc.numpy()
ax = sns.kdeplot(loc_[:,0,0], loc_[:,0,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,1,0], loc_[:,1,1], shade=True, shade_lowest=False)
ax = sns.kdeplot(loc_[:,2,0], loc_[:,2,1], shade=True, shade_lowest=False)
plt.title('KDE of loc draws');
结论
这个简单的 colab 演示了如何使用 TensorFlow Probability 原语来构建分层贝叶斯混合模型。
