 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
JAX 上的 TensorFlow Probability (TFP) 现在拥有用于分布式数值计算的工具。为了扩展到大量加速器,这些工具是围绕使用“单程序多数据”范式(简称 SPMD)编写代码而构建的。
在本笔记本中,我们将介绍如何“以 SPMD 方式思考”,并介绍用于扩展到 TPU Pod 或 GPU 集群等配置的新 TFP 抽象。如果您自己运行此代码,请确保选择 TPU 运行时。
首先,我们将安装最新版本的 TFP、JAX 和 TF。
安装
我们将导入一些通用库,以及一些 JAX 实用程序。
设置和导入
INFO:tensorflow:Enabling eager execution INFO:tensorflow:Enabling v2 tensorshape INFO:tensorflow:Enabling resource variables INFO:tensorflow:Enabling tensor equality INFO:tensorflow:Enabling control flow v2
我们还将设置一些方便的 TFP 别名。新的抽象目前在 tfp.experimental.distribute 和 tfp.experimental.mcmc 中提供。
tfd = tfp.distributions
tfb = tfp.bijectors
tfm = tfp.mcmc
tfed = tfp.experimental.distribute
tfde = tfp.experimental.distributions
tfem = tfp.experimental.mcmc
Root = tfed.JointDistributionCoroutine.Root
要将笔记本连接到 TPU,我们使用 JAX 中的以下辅助程序。为了确认我们已连接,我们将打印出设备数量,它应该是八个。
from jax.tools import colab_tpu
colab_tpu.setup_tpu()
print(f'Found {jax.device_count()} devices')
Found 8 devices
快速介绍 jax.pmap
连接到 TPU 后,我们可以访问 *八个* 设备。但是,当我们急切地运行 JAX 代码时,JAX 默认只在一个设备上运行计算。
跨多个设备执行计算的最简单方法是映射一个函数,让每个设备执行映射中的一个索引。JAX 提供了 jax.pmap(“并行映射”)转换,它将函数转换为一个跨多个设备映射函数的函数。
在以下示例中,我们创建一个大小为 8 的数组(与可用设备数量匹配),并映射一个在其中添加 5 的函数。
xs = jnp.arange(8.)
out = jax.pmap(lambda x: x + 5.)(xs)
print(type(out), out)
<class 'jax.interpreters.pxla.ShardedDeviceArray'> [ 5. 6. 7. 8. 9. 10. 11. 12.]
请注意,我们收到了一个 ShardedDeviceArray 类型,表明输出数组在物理上跨设备分割。
jax.pmap 在语义上类似于映射,但它有一些重要的选项可以修改其行为。默认情况下,pmap 假设函数的所有输入都将被映射,但我们可以使用 in_axes 参数修改此行为。
xs = jnp.arange(8.)
y = 5.
# Map over the 0-axis of `xs` and don't map over `y`
out = jax.pmap(lambda x, y: x + y, in_axes=(0, None))(xs, y)
print(out)
[ 5. 6. 7. 8. 9. 10. 11. 12.]
类似地,pmap 的 out_axes 参数决定是否在每个设备上返回这些值。将 out_axes 设置为 None 会自动在第一个设备上返回该值,并且仅应在确信每个设备上的值都相同的情况下使用。
xs = jnp.ones(8) # Value is the same on each device
out = jax.pmap(lambda x: x + 1, out_axes=None)(xs)
print(out)
2.0
如果我们想要做的事情不容易用映射的纯函数来表达,会发生什么?例如,如果我们想在我们要映射的轴上进行求和,该怎么办?JAX 提供了“集合”,这些函数跨设备进行通信,以实现编写更有趣和更复杂的分布式程序。为了了解它们的工作原理,我们将介绍 SPMD。
什么是 SPMD?
单程序多数据 (SPMD) 是一种并发编程模型,其中单个程序(即相同的代码)在多个设备上同时执行,但每个正在运行的程序的输入可能不同。
如果我们的程序是其输入的简单函数(例如类似于 x + 5 的东西),那么在 SPMD 中运行程序只是将它映射到不同的数据上,就像我们之前使用 jax.pmap 所做的那样。但是,我们可以做的不仅仅是“映射”一个函数。JAX 提供了“集体操作”,它们是跨设备通信的函数。
例如,我们可能希望获取所有设备上某个量的总和。在执行此操作之前,我们需要为我们在 pmap 中映射的轴分配一个名称。然后,我们使用 lax.psum(“并行求和”)函数跨设备执行求和,确保我们识别出我们要求和的命名轴。
def f(x):
out = lax.psum(x, axis_name='i')
return out
xs = jnp.arange(8.) # Length of array matches number of devices
jax.pmap(f, axis_name='i')(xs)
ShardedDeviceArray([28., 28., 28., 28., 28., 28., 28., 28.], dtype=float32)
psum 集体操作聚合每个设备上 x 的值,并在映射中同步其值,即 out 在每个设备上都是 28. 。我们不再执行简单的“映射”,而是执行一个 SPMD 程序,其中每个设备的计算现在可以与其他设备上的相同计算进行交互,尽管使用集体操作的方式有限。在这种情况下,我们可以使用 out_axes = None,因为 psum 将同步该值。
def f(x):
out = lax.psum(x, axis_name='i')
return out
jax.pmap(f, axis_name='i', out_axes=None)(jnp.arange(8.))
ShardedDeviceArray(28., dtype=float32)
SPMD 使我们能够编写一个程序,该程序可以在任何 TPU 配置中同时在每个设备上运行。用于在 8 个 TPU 内核上执行机器学习的相同代码也可以用于可能拥有数百到数千个内核的 TPU pod!有关 jax.pmap 和 SPMD 的更详细教程,您可以参考 JAX 101 教程。
大规模 MCMC
在本笔记本中,我们重点介绍使用马尔可夫链蒙特卡罗 (MCMC) 方法进行贝叶斯推断。我们可以利用许多设备来执行 MCMC,但本笔记本中,我们将重点介绍两种方法
- 在不同设备上运行独立的马尔可夫链。这种情况相当简单,可以使用普通的 TFP 来实现。
- 跨设备对数据集进行分片。这种情况稍微复杂一些,需要最近添加的 TFP 机制。
独立链
假设我们希望使用 MCMC 对问题进行贝叶斯推断,并且希望在多个设备上并行运行多个链(例如,每个设备上运行 2 个链)。事实证明,这是一个我们可以跨设备“映射”的程序,即不需要任何集体操作的程序。为了确保每个程序执行不同的马尔可夫链(而不是运行相同的链),我们将不同的随机种子值传递给每个设备。
让我们尝试在一个从二维高斯分布中采样的玩具问题上进行尝试。我们可以直接使用 TFP 现有的 MCMC 功能。通常,我们会尝试将大部分逻辑放在映射函数内部,以便更明确地区分在所有设备上运行的内容与仅在第一个设备上运行的内容。
def run(seed):
target_log_prob = tfd.Sample(tfd.Normal(0., 1.), 2).log_prob
initial_state = jnp.zeros([2, 2]) # 2 chains
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-1, 10)
def trace_fn(state, pkr):
return target_log_prob(state)
states, log_prob = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
kernel=kernel,
current_state=initial_state,
trace_fn=trace_fn,
seed=seed
)
return states, log_prob
run 函数本身接受一个无状态随机种子(要了解无状态随机性的工作原理,您可以阅读 JAX 上的 TFP 笔记本或查看 JAX 101 教程)。在不同的种子值上映射 run 将导致运行多个独立的马尔可夫链。
states, log_probs = jax.pmap(run)(random.split(random.PRNGKey(0), 8))
print(states.shape, log_probs.shape)
# states is (8 devices, 1000 samples, 2 chains, 2 dimensions)
# log_prob is (8 devices, 1000 samples, 2 chains)
(8, 1000, 2, 2) (8, 1000, 2)
请注意,我们现在有一个额外的轴,对应于每个设备。我们可以重新排列维度并将其展平,以获得 16 个链的轴。
states = states.transpose([0, 2, 1, 3]).reshape([-1, 1000, 2])
log_probs = log_probs.transpose([0, 2, 1]).reshape([-1, 1000])
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].plot(log_probs.T, alpha=0.4)
ax[1].scatter(*states.reshape([-1, 2]).T, alpha=0.1)
plt.show()
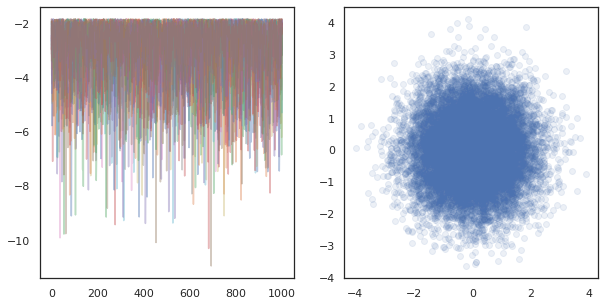
在许多设备上运行独立链时,就像在使用 tfp.mcmc 的函数上执行 pmap 一样简单,确保我们将不同的随机种子值传递给每个设备。
对数据进行分片
当我们执行 MCMC 时,目标分布通常是通过对数据集进行条件化而获得的后验分布,并且计算非归一化对数密度涉及对每个观察到的数据的似然进行求和。
对于非常大的数据集,即使在单个设备上运行一个链也可能非常昂贵。但是,当我们能够访问多个设备时,我们可以将数据集拆分到这些设备上,以更好地利用我们可用的计算能力。
如果我们希望使用分片数据集执行 MCMC,我们需要确保我们在每个设备上计算的非归一化对数密度代表总密度,即所有数据的密度,否则每个设备将使用自己的不正确的目标分布执行 MCMC。为此,TFP 现在提供了一些新工具(即 tfp.experimental.distribute 和 tfp.experimental.mcmc),这些工具使我们能够计算“分片”对数概率并使用它们执行 MCMC。
分片分布
TFP 现在提供的用于计算分片对数概率的核心抽象是 Sharded 元分布,它接受一个分布作为输入,并返回一个新的分布,该分布在 SPMD 上下文中执行时具有特定的属性。 Sharded 位于 tfp.experimental.distribute 中。
直观地说, Sharded 分布对应于一组跨设备“拆分”的随机变量。在每个设备上,它们将生成不同的样本,并且可以分别具有不同的对数密度。或者, Sharded 分布对应于图形模型术语中的“板”,其中板的大小是设备的数量。
从 Sharded 分布中采样
如果我们在使用每个设备上相同种子的 pmap 的程序中从 Normal 分布中采样,我们将在每个设备上获得相同的样本。我们可以将以下函数视为对跨设备同步的单个随机变量进行采样。
# `pmap` expects at least one value to be mapped over, so we provide a dummy one
def f(seed, _):
return tfd.Normal(0., 1.).sample(seed=seed)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32)
如果我们使用 tfed.Sharded 包装 tfd.Normal(0., 1.),我们从逻辑上讲现在有八个不同的随机变量(每个设备上一个),因此将为每个变量生成不同的样本,尽管传递了相同的种子。
def f(seed, _):
return tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i').sample(seed=seed)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
ShardedDeviceArray([ 1.2152631 , 0.7818249 , 0.32549605, 0.6828047 ,
1.3973192 , -0.57830244, 0.37862757, 2.7706041 ], dtype=float32)
此分布在单个设备上的等效表示只是 8 个独立的正态样本。即使样本的值将不同( tfed.Sharded 对伪随机数生成略有不同),它们都代表相同的分布。
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.sample(seed=random.PRNGKey(0))
DeviceArray([ 0.08086783, -0.38624594, -0.3756545 , 1.668957 ,
-1.2758069 , 2.1192007 , -0.85821325, 1.1305912 ], dtype=float32)
获取 Sharded 分布的对数密度
让我们看看当我们在 SPMD 上下文中计算来自常规分布的样本的对数密度时会发生什么。
def f(seed, _):
dist = tfd.Normal(0., 1.)
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0))(random.PRNGKey(0), jnp.arange(8.))
(ShardedDeviceArray([-0.20584236, -0.20584236, -0.20584236, -0.20584236,
-0.20584236, -0.20584236, -0.20584236, -0.20584236], dtype=float32),
ShardedDeviceArray([-0.94012403, -0.94012403, -0.94012403, -0.94012403,
-0.94012403, -0.94012403, -0.94012403, -0.94012403], dtype=float32))
每个样本在每个设备上都是相同的,因此我们也在每个设备上计算相同的密度。直观地说,这里我们只有一个关于单个正态分布变量的分布。
对于 Sharded 分布,我们有一个关于 8 个随机变量的分布,因此当我们计算样本的 log_prob 时,我们在设备上对每个单独的对数密度进行求和。(您可能会注意到,此总的 log_prob 值大于上面计算的单例 log_prob。)
def f(seed, _):
dist = tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i')
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
sample, log_prob = jax.pmap(f, in_axes=(None, 0), axis_name='i')(
random.PRNGKey(0), jnp.arange(8.))
print('Sample:', sample)
print('Log Prob:', log_prob)
Sample: [ 1.2152631 0.7818249 0.32549605 0.6828047 1.3973192 -0.57830244 0.37862757 2.7706041 ] Log Prob: [-13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205 -13.7349205]
等效的“非分片”分布会生成相同对数密度。
dist = tfd.Sample(tfd.Normal(0., 1.), jax.device_count())
dist.log_prob(sample)
DeviceArray(-13.7349205, dtype=float32)
Sharded 分布在每个设备上从 sample 生成不同的值,但在每个设备上获得 log_prob 的相同值。这里发生了什么? Sharded 分布在内部执行 psum 以确保 log_prob 值在设备之间同步。为什么我们要这种行为?如果我们在每个设备上运行相同的 MCMC 链,我们希望 target_log_prob 在每个设备上都相同,即使计算中的一些随机变量在设备之间进行分片。
此外, Sharded 分布确保设备之间的梯度是正确的,以确保像 HMC 这样的算法(将对数密度函数的梯度作为转换函数的一部分)生成正确的样本。
分片 JointDistribution
我们可以通过使用 JointDistribution(JD)来创建具有多个 Sharded 随机变量的模型。不幸的是, Sharded 分布不能与普通的 tfd.JointDistribution 安全地一起使用,但 tfp.experimental.distribute 导出了“修补”的 JD,这些 JD 将表现得像 Sharded 分布。
def f(seed, _):
dist = tfed.JointDistributionSequential([
tfd.Normal(0., 1.),
tfed.Sharded(tfd.Normal(0., 1.), shard_axis_name='i'),
])
x = dist.sample(seed=seed)
return x, dist.log_prob(x)
jax.pmap(f, in_axes=(None, 0), axis_name='i')(random.PRNGKey(0), jnp.arange(8.))
([ShardedDeviceArray([1.6121525, 1.6121525, 1.6121525, 1.6121525, 1.6121525,
1.6121525, 1.6121525, 1.6121525], dtype=float32),
ShardedDeviceArray([ 0.8690128 , -0.83167845, 1.2209264 , 0.88412696,
0.76478404, -0.66208494, -0.0129658 , 0.7391483 ], dtype=float32)],
ShardedDeviceArray([-12.214451, -12.214451, -12.214451, -12.214451,
-12.214451, -12.214451, -12.214451, -12.214451], dtype=float32))
这些分片 JD 可以具有 Sharded 和普通 TFP 分布作为组件。对于非分片分布,我们在每个设备上获得相同的样本,对于分片分布,我们获得不同的样本。每个设备上的 log_prob 也会同步。
使用 Sharded 分布执行 MCMC
我们如何在 MCMC 的上下文中考虑 Sharded 分布?如果我们有一个可以表示为 JointDistribution 的生成模型,我们可以选择该模型的某个轴进行“分片”。通常,模型中的一个随机变量将对应于观察到的数据,如果我们有一个我们希望跨设备进行分片的大型数据集,我们希望与数据点相关联的变量也进行分片。我们可能还有一些与我们正在分片的观察结果一一对应的“局部”随机变量,因此我们还需要对这些随机变量进行分片。
在本节中,我们将介绍使用 Sharded 分布与 TFP MCMC 的示例。我们将从一个更简单的贝叶斯逻辑回归示例开始,最后以矩阵分解示例结束,目的是展示 distribute 库的一些用例。
示例:用于 MNIST 的贝叶斯逻辑回归
我们希望对大型数据集执行贝叶斯逻辑回归;该模型对回归权重具有先验 \(p(\theta)\),并且似然 \(p(y_i | \theta, x_i)\) 在所有数据 \(\{x_i, y_i\}_{i = 1}^N\) 上求和以获得总的联合对数密度。如果我们对数据进行分片,我们将对模型中观察到的随机变量 \(x_i\) 和 \(y_i\) 进行分片。
我们使用以下贝叶斯逻辑回归模型进行 MNIST 分类
\[ \begin{align*} w &\sim \mathcal{N}(0, 1) \\ b &\sim \mathcal{N}(0, 1) \\ y_i | w, b, x_i &\sim \textrm{Categorical}(w^T x_i + b) \end{align*} \]
让我们使用 TensorFlow Datasets 加载 MNIST。
mnist = tfds.as_numpy(tfds.load('mnist', batch_size=-1))
raw_train_images, train_labels = mnist['train']['image'], mnist['train']['label']
train_images = raw_train_images.reshape([raw_train_images.shape[0], -1]) / 255.
raw_test_images, test_labels = mnist['test']['image'], mnist['test']['label']
test_images = raw_test_images.reshape([raw_test_images.shape[0], -1]) / 255.
Downloading and preparing dataset mnist/3.0.1 (download: 11.06 MiB, generated: 21.00 MiB, total: 32.06 MiB) to /root/tensorflow_datasets/mnist/3.0.1... WARNING:absl:Dataset mnist is hosted on GCS. It will automatically be downloaded to your local data directory. If you'd instead prefer to read directly from our public GCS bucket (recommended if you're running on GCP), you can instead pass `try_gcs=True` to `tfds.load` or set `data_dir=gs://tfds-data/datasets`. HBox(children=(FloatProgress(value=0.0, description='Dl Completed...', max=4.0, style=ProgressStyle(descriptio… Dataset mnist downloaded and prepared to /root/tensorflow_datasets/mnist/3.0.1. Subsequent calls will reuse this data.
我们有 60000 张训练图像,但让我们利用我们可用的 8 个内核并将它们拆分为 8 个部分。我们将使用这个方便的 shard 实用函数。
def shard_value(x):
x = x.reshape((jax.device_count(), -1, *x.shape[1:]))
return jax.pmap(lambda x: x)(x) # pmap will physically place values on devices
shard = functools.partial(jax.tree.map, shard_value)
sharded_train_images, sharded_train_labels = shard((train_images, train_labels))
print(sharded_train_images.shape, sharded_train_labels.shape)
(8, 7500, 784) (8, 7500)
在继续之前,让我们快速讨论一下 TPU 上的精度及其对 HMC 的影响。TPU 使用低 bfloat16 精度执行矩阵乘法以提高速度。 bfloat16 矩阵乘法通常足以满足许多深度学习应用,但在与 HMC 一起使用时,我们通过实验证明,较低的精度会导致轨迹发散,从而导致拒绝。我们可以使用更高精度的矩阵乘法,但会付出一些额外的计算成本。
为了提高我们的矩阵乘法精度,我们可以使用 jax.default_matmul_precision 装饰器,并使用 "tensorfloat32" 精度(对于更高的精度,我们可以使用 "float32" 精度)。
现在让我们定义我们的 run 函数,该函数将接收一个随机种子(在每个设备上都相同)和一个 MNIST 分片。该函数将实现上述模型,然后我们将使用 TFP 的普通 MCMC 功能运行单个链。我们将确保用 jax.default_matmul_precision 装饰器装饰 run,以确保矩阵乘法以更高的精度运行,尽管在下面的特定示例中,我们也可以使用 jnp.dot(images, w, precision=lax.Precision.HIGH)。
# We can use `out_axes=None` in the `pmap` because the results will be the same
# on every device.
@functools.partial(jax.pmap, axis_name='data', in_axes=(None, 0), out_axes=None)
@jax.default_matmul_precision('tensorfloat32')
def run(seed, data):
images, labels = data # a sharded dataset
num_examples, dim = images.shape
num_classes = 10
def model_fn():
w = yield Root(tfd.Sample(tfd.Normal(0., 1.), [dim, num_classes]))
b = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_classes]))
logits = jnp.dot(images, w) + b
yield tfed.Sharded(tfd.Independent(tfd.Categorical(logits=logits), 1),
shard_axis_name='data')
model = tfed.JointDistributionCoroutine(model_fn)
init_seed, sample_seed = random.split(seed)
initial_state = model.sample(seed=init_seed)[:-1] # throw away `y`
def target_log_prob(*state):
return model.log_prob((*state, labels))
def accuracy(w, b):
logits = images.dot(w) + b
preds = logits.argmax(axis=-1)
# We take the average accuracy across devices by using `lax.pmean`
return lax.pmean((preds == labels).mean(), 'data')
kernel = tfm.HamiltonianMonteCarlo(target_log_prob, 1e-2, 100)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, 500)
def trace_fn(state, pkr):
return (
target_log_prob(*state),
accuracy(*state),
pkr.new_step_size)
states, trace = tfm.sample_chain(
num_results=1000,
num_burnin_steps=1000,
current_state=initial_state,
kernel=kernel,
trace_fn=trace_fn,
seed=sample_seed
)
return states, trace
jax.pmap 包含一个 JIT 编译,但编译后的函数在第一次调用后会被缓存。我们将调用 run 并忽略输出以缓存编译。
%%time
output = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree.map(lambda x: x.block_until_ready(), output)
CPU times: user 24.5 s, sys: 48.2 s, total: 1min 12s Wall time: 1min 54s
现在我们将再次调用 run,以查看实际执行需要多长时间。
%%time
states, trace = run(random.PRNGKey(0), (sharded_train_images, sharded_train_labels))
jax.tree.map(lambda x: x.block_until_ready(), trace)
CPU times: user 13.1 s, sys: 45.2 s, total: 58.3 s Wall time: 1min 43s
我们正在执行 200,000 个跳跃蛙步骤,每个步骤都会计算整个数据集上的梯度。将计算分散到 8 个核心上使我们能够在约 95 秒内计算相当于 200,000 个训练周期的计算量,大约每秒 2,100 个周期!
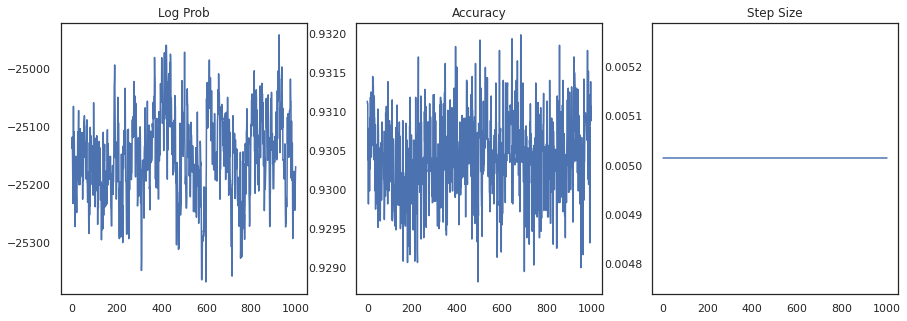
让我们绘制每个样本的对数密度和每个样本的准确率
fig, ax = plt.subplots(1, 3, figsize=(15, 5))
ax[0].plot(trace[0])
ax[0].set_title('Log Prob')
ax[1].plot(trace[1])
ax[1].set_title('Accuracy')
ax[2].plot(trace[2])
ax[2].set_title('Step Size')
plt.show()
如果我们对样本进行集成,我们可以计算贝叶斯模型平均值以提高我们的性能。
@functools.partial(jax.pmap, axis_name='data', in_axes=(0, None), out_axes=None)
def bayesian_model_average(data, states):
images, labels = data
logits = jax.vmap(lambda w, b: images.dot(w) + b)(*states)
probs = jax.nn.softmax(logits, axis=-1)
bma_accuracy = (probs.mean(axis=0).argmax(axis=-1) == labels).mean()
avg_accuracy = (probs.argmax(axis=-1) == labels).mean()
return lax.pmean(bma_accuracy, axis_name='data'), lax.pmean(avg_accuracy, axis_name='data')
sharded_test_images, sharded_test_labels = shard((test_images, test_labels))
bma_acc, avg_acc = bayesian_model_average((sharded_test_images, sharded_test_labels), states)
print(f'Average Accuracy: {avg_acc}')
print(f'BMA Accuracy: {bma_acc}')
print(f'Accuracy Improvement: {bma_acc - avg_acc}')
Average Accuracy: 0.9188529253005981 BMA Accuracy: 0.9264000058174133 Accuracy Improvement: 0.0075470805168151855
贝叶斯模型平均值将我们的准确率提高了近 1%!
示例:MovieLens 推荐系统
现在让我们尝试使用 MovieLens 推荐数据集进行推理,该数据集是用户及其对各种电影的评分的集合。具体来说,我们可以将 MovieLens 表示为一个 \(N \times M\) 观看矩阵 \(W\),其中 \(N\) 是用户数量,\(M\) 是电影数量;我们期望 \(N > M\)。\(W_{ij}\) 的条目是一个布尔值,指示用户 \(i\) 是否观看过电影 \(j\)。请注意,MovieLens 提供了用户评分,但为了简化问题,我们忽略了它们。
首先,我们将加载数据集。我们将使用包含 100 万个评分的版本。
movielens = tfds.as_numpy(tfds.load('movielens/1m-ratings', batch_size=-1))
GENRES = ['Action', 'Adventure', 'Animation', 'Children', 'Comedy',
'Crime', 'Documentary', 'Drama', 'Fantasy', 'Film-Noir',
'Horror', 'IMAX', 'Musical', 'Mystery', 'Romance', 'Sci-Fi',
'Thriller', 'Unknown', 'War', 'Western', '(no genres listed)']
Downloading and preparing dataset movielens/1m-ratings/0.1.0 (download: Unknown size, generated: Unknown size, total: Unknown size) to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0... HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Completed...', max=1.0, style=Progre… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Dl Size...', max=1.0, style=ProgressSty… HBox(children=(FloatProgress(value=1.0, bar_style='info', description='Extraction completed...', max=1.0, styl… HBox(children=(FloatProgress(value=1.0, bar_style='info', max=1.0), HTML(value=''))) Shuffling and writing examples to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0.incompleteYKA3TG/movielens-train.tfrecord HBox(children=(FloatProgress(value=0.0, max=1000209.0), HTML(value=''))) Dataset movielens downloaded and prepared to /root/tensorflow_datasets/movielens/1m-ratings/0.1.0. Subsequent calls will reuse this data.
我们将对数据集进行一些预处理以获得观看矩阵 \(W\)。
raw_movie_ids = movielens['train']['movie_id']
raw_user_ids = movielens['train']['user_id']
genres = movielens['train']['movie_genres']
movie_ids, movie_labels = pd.factorize(movielens['train']['movie_id'])
user_ids, user_labels = pd.factorize(movielens['train']['user_id'])
num_movies = movie_ids.max() + 1
num_users = user_ids.max() + 1
movie_titles = dict(zip(movielens['train']['movie_id'],
movielens['train']['movie_title']))
movie_genres = dict(zip(movielens['train']['movie_id'],
genres))
movie_id_to_title = [movie_titles[movie_labels[id]].decode('utf-8')
for id in range(num_movies)]
movie_id_to_genre = [GENRES[movie_genres[movie_labels[id]][0]] for id in range(num_movies)]
watch_matrix = np.zeros((num_users, num_movies), bool)
watch_matrix[user_ids, movie_ids] = True
print(watch_matrix.shape)
(6040, 3706)
我们可以使用简单的概率矩阵分解模型定义 \(W\) 的生成模型。我们假设一个潜在的 \(N \times D\) 用户矩阵 \(U\) 和一个潜在的 \(M \times D\) 电影矩阵 \(V\),当它们相乘时会生成观看矩阵 \(W\) 的伯努利对数。我们还将为用户和电影包含一个偏差向量,即 \(u\) 和 \(v\)。
\[ \begin{align*} U &\sim \mathcal{N}(0, 1) \quad u \sim \mathcal{N}(0, 1)\\ V &\sim \mathcal{N}(0, 1) \quad v \sim \mathcal{N}(0, 1)\\ W_{ij} &\sim \textrm{Bernoulli}\left(\sigma\left(\left(UV^T\right)_{ij} + u_i + v_j\right)\right) \end{align*} \]
这是一个相当大的矩阵;6040 个用户和 3706 部电影导致一个矩阵,其中包含超过 2200 万个条目。我们如何处理对该模型进行分片?好吧,如果我们假设 \(N > M\)(即用户比电影多),那么将观看矩阵跨用户轴进行分片是有意义的,因此每个设备将拥有对应于用户子集的观看矩阵的一部分。但是,与前面的示例不同,我们还需要对 \(U\) 矩阵进行分片,因为它包含每个用户的嵌入,因此每个设备将负责 \(U\) 的一部分和 \(W\) 的一部分。另一方面,\(V\) 将不会被分片,并且将在所有设备之间同步。
sharded_watch_matrix = shard(watch_matrix)
在我们编写 run 之前,让我们快速讨论一下对局部随机变量 \(U\) 进行分片的额外挑战。在运行 HMC 时,普通 tfp.mcmc.HamiltonianMonteCarlo 内核将为链状态的每个元素采样动量。以前,只有未分片的随机变量是该状态的一部分,并且动量在每个设备上都是相同的。当我们现在有一个分片的 \(U\) 时,我们需要在每个设备上为 \(U\) 采样不同的动量,同时为 \(V\) 采样相同的动量。为了实现这一点,我们可以使用 tfp.experimental.mcmc.PreconditionedHamiltonianMonteCarlo,并使用 Sharded 动量分布。随着我们继续使并行计算成为一等公民,我们可能会简化这一点,例如通过将分片指示器传递给 HMC 内核。
def make_run(*,
axis_name,
dim=20,
num_chains=2,
prior_variance=1.,
step_size=1e-2,
num_leapfrog_steps=100,
num_burnin_steps=1000,
num_results=500,
):
@functools.partial(jax.pmap, in_axes=(None, 0), axis_name=axis_name)
@jax.default_matmul_precision('tensorfloat32')
def run(key, watch_matrix):
num_users, num_movies = watch_matrix.shape
Sharded = functools.partial(tfed.Sharded, shard_axis_name=axis_name)
def prior_fn():
user_embeddings = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users, dim]), name='user_embeddings'))
user_bias = yield Root(Sharded(tfd.Sample(tfd.Normal(0., 1.), [num_users]), name='user_bias'))
movie_embeddings = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies, dim], name='movie_embeddings'))
movie_bias = yield Root(tfd.Sample(tfd.Normal(0., 1.), [num_movies], name='movie_bias'))
return (user_embeddings, user_bias, movie_embeddings, movie_bias)
prior = tfed.JointDistributionCoroutine(prior_fn)
def model_fn():
user_embeddings, user_bias, movie_embeddings, movie_bias = yield from prior_fn()
logits = (jnp.einsum('...nd,...md->...nm', user_embeddings, movie_embeddings)
+ user_bias[..., :, None] + movie_bias[..., None, :])
yield Sharded(tfd.Independent(tfd.Bernoulli(logits=logits), 2), name='watch')
model = tfed.JointDistributionCoroutine(model_fn)
init_key, sample_key = random.split(key)
initial_state = prior.sample(seed=init_key, sample_shape=num_chains)
def target_log_prob(*state):
return model.log_prob((*state, watch_matrix))
momentum_distribution = tfed.JointDistributionSequential([
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users, dim]), 1.), 2)),
Sharded(tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_users]), 1.), 1)),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies, dim]), 1.), 2),
tfd.Independent(tfd.Normal(jnp.zeros([num_chains, num_movies]), 1.), 1),
])
# We pass in momentum_distribution here to ensure that the momenta for
# user_embeddings and user_bias are also sharded
kernel = tfem.PreconditionedHamiltonianMonteCarlo(target_log_prob, step_size,
num_leapfrog_steps,
momentum_distribution=momentum_distribution)
num_adaptation_steps = int(0.8 * num_burnin_steps)
kernel = tfm.DualAveragingStepSizeAdaptation(kernel, num_adaptation_steps)
def trace_fn(state, pkr):
return {
'log_prob': target_log_prob(*state),
'log_accept_ratio': pkr.inner_results.log_accept_ratio,
}
return tfm.sample_chain(
num_results, initial_state,
kernel=kernel,
num_burnin_steps=num_burnin_steps,
trace_fn=trace_fn,
seed=sample_key)
return run
我们将再次运行它一次以缓存编译后的 run。
%%time
run = make_run(axis_name='data')
output = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree.map(lambda x: x.block_until_ready(), output)
CPU times: user 56 s, sys: 1min 24s, total: 2min 20s Wall time: 3min 35s
现在我们将再次运行它,但没有编译开销。
%%time
states, trace = run(random.PRNGKey(0), sharded_watch_matrix)
jax.tree.map(lambda x: x.block_until_ready(), trace)
CPU times: user 28.8 s, sys: 1min 16s, total: 1min 44s Wall time: 3min 1s
看起来我们在大约 3 分钟内完成了大约 150,000 个跳跃蛙步骤,因此大约每秒 83 个跳跃蛙步骤!让我们绘制样本的接受率和对数密度。
fig, axs = plt.subplots(1, len(trace), figsize=(5 * len(trace), 5))
for ax, (key, val) in zip(axs, trace.items()):
ax.plot(val[0]) # Indexing into a sharded array, each element is the same
ax.set_title(key);
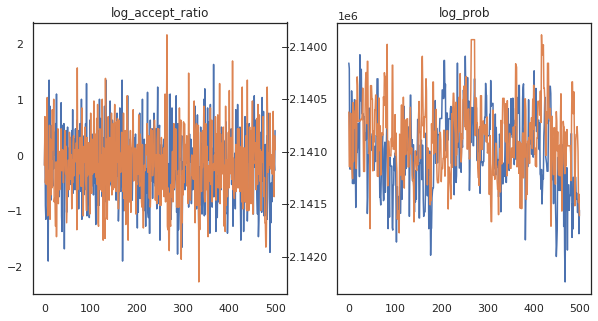
现在我们已经从马尔可夫链中获得了一些样本,让我们使用它们进行一些预测。首先,让我们提取每个组件。请记住,user_embeddings 和 user_bias 在设备之间是分片的,因此我们需要连接我们的 ShardedArray 以获得所有这些。另一方面,movie_embeddings 和 movie_bias 在每个设备上都是相同的,因此我们可以只从第一个分片中选择值。我们将使用常规的 numpy 将值从 TPU 复制回 CPU。
user_embeddings = np.concatenate(np.array(states.user_embeddings, np.float32), axis=2)
user_bias = np.concatenate(np.array(states.user_bias, np.float32), axis=2)
movie_embeddings = np.array(states.movie_embeddings[0], dtype=np.float32)
movie_bias = np.array(states.movie_bias[0], dtype=np.float32)
samples = (user_embeddings, user_bias, movie_embeddings, movie_bias)
print(f'User embeddings: {user_embeddings.shape}')
print(f'User bias: {user_bias.shape}')
print(f'Movie embeddings: {movie_embeddings.shape}')
print(f'Movie bias: {movie_bias.shape}')
User embeddings: (500, 2, 6040, 20) User bias: (500, 2, 6040) Movie embeddings: (500, 2, 3706, 20) Movie bias: (500, 2, 3706)
让我们尝试构建一个简单的推荐系统,该系统利用这些样本中捕获的不确定性。让我们首先编写一个函数,该函数根据观看概率对电影进行排名。
@jax.jit
def recommend(sample, user_id):
user_embeddings, user_bias, movie_embeddings, movie_bias = sample
movie_logits = (
jnp.einsum('d,md->m', user_embeddings[user_id], movie_embeddings)
+ user_bias[user_id] + movie_bias)
return movie_logits.argsort()[::-1]
现在我们可以编写一个函数,该函数循环遍历所有样本,并为每个样本选择用户尚未观看的排名最高的电影。然后我们可以查看所有推荐电影在样本中的计数。
def get_recommendations(user_id):
movie_ids = []
already_watched = set(jnp.arange(num_movies)[watch_matrix[user_id] == 1])
for i in range(500):
for j in range(2):
sample = jax.tree.map(lambda x: x[i, j], samples)
ranking = recommend(sample, user_id)
for movie_id in ranking:
if int(movie_id) not in already_watched:
movie_ids.append(movie_id)
break
return movie_ids
def plot_recommendations(movie_ids, ax=None):
titles = collections.Counter([movie_id_to_title[i] for i in movie_ids])
ax = ax or plt.gca()
names, counts = zip(*sorted(titles.items(), key=lambda x: -x[1]))
ax.bar(names, counts)
ax.set_xticklabels(names, rotation=90)
让我们看看观看电影最多的用户和观看电影最少的用户。
user_watch_counts = watch_matrix.sum(axis=1)
user_most = user_watch_counts.argmax()
user_least = user_watch_counts.argmin()
print(user_watch_counts[user_most], user_watch_counts[user_least])
2314 20
我们希望我们的系统对 user_most 比对 user_least 更有把握,因为我们对 user_most 更可能观看的电影类型有更多信息。
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
most_recommendations = get_recommendations(user_most)
plot_recommendations(most_recommendations, ax=ax[0])
ax[0].set_title('Recommendation for user_most')
least_recommendations = get_recommendations(user_least)
plot_recommendations(least_recommendations, ax=ax[1])
ax[1].set_title('Recommendation for user_least');
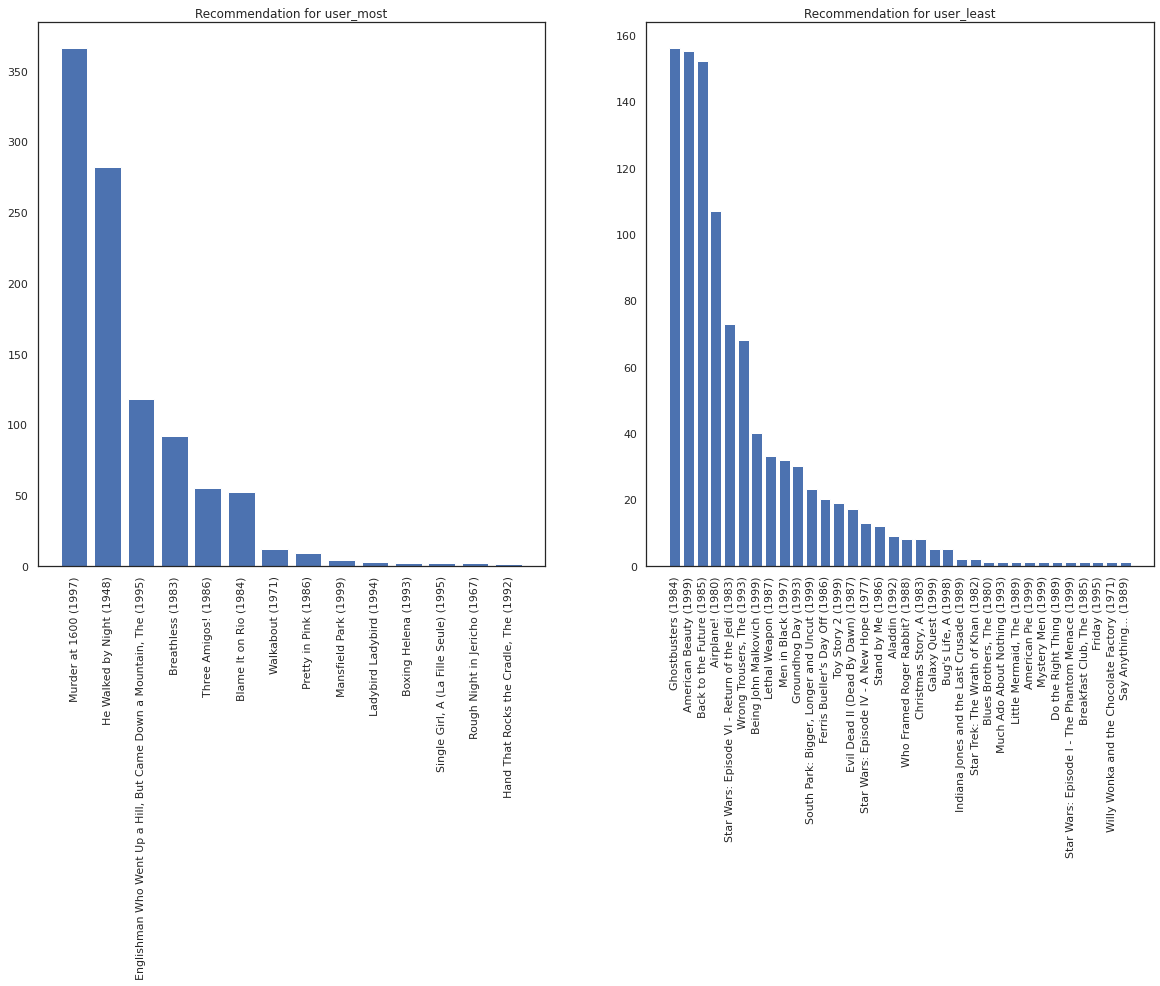
我们看到,我们对 user_least 的推荐存在更多差异,反映了我们对其观看偏好的额外不确定性。
我们还可以查看推荐电影的类型。
most_genres = collections.Counter([movie_id_to_genre[i] for i in most_recommendations])
least_genres = collections.Counter([movie_id_to_genre[i] for i in least_recommendations])
fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].bar(most_genres.keys(), most_genres.values())
ax[0].set_title('Genres recommended for user_most')
ax[1].bar(least_genres.keys(), least_genres.values())
ax[1].set_title('Genres recommended for user_least');
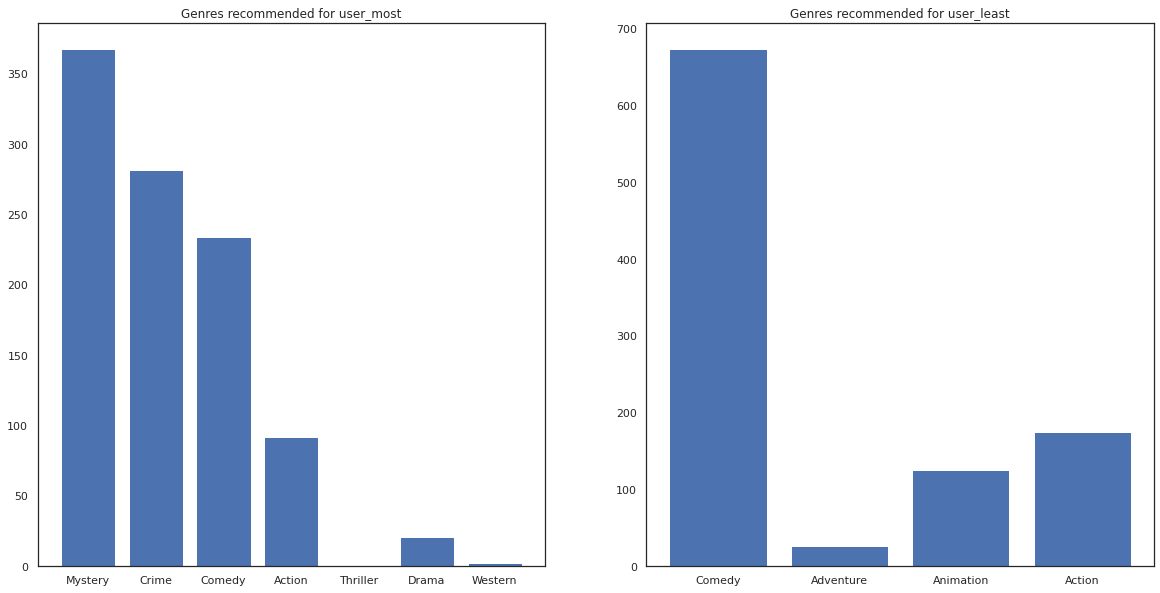
user_most 已经观看过很多电影,并且被推荐了更多利基类型,例如悬疑和犯罪,而 user_least 还没有观看过很多电影,并且被推荐了更多主流电影,这些电影倾向于喜剧和动作。
