 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
本教程演示了如何使用 TensorFlow 实现 Actor-Critic 方法,以在 Open AI Gym CartPole-v0 环境中训练代理。假设读者对 策略梯度方法 或 (深度)强化学习 有所了解。
Actor-Critic 方法
Actor-Critic 方法是 时序差分 (TD) 学习 方法,它独立于价值函数表示策略函数。
策略函数(或策略)根据给定状态返回代理可以采取的动作的概率分布。价值函数确定代理从给定状态开始并根据特定策略永远行动的预期回报。
在 Actor-Critic 方法中,策略被称为Actor,它根据状态提出了一组可能的动作,而估计的价值函数被称为Critic,它根据给定策略评估Actor采取的动作。
在本教程中,Actor 和 Critic 将使用一个具有两个输出的神经网络来表示。
CartPole-v0
在 CartPole-v0 环境 中,一根杆子连接到一个在无摩擦轨道上移动的小车上。杆子最初是直立的,代理的目标是通过对小车施加 -1 或 +1 的力来防止它倒下。每次杆子保持直立的时间步长都会获得 +1 的奖励。当以下情况发生时,一集结束:1) 杆子与垂直方向的夹角超过 15 度;或 2) 小车从中心移动超过 2.4 个单位。

当一集的平均总奖励在连续 100 次试验中达到 195 时,该问题被认为是“解决”的。
设置
导入必要的包并配置全局设置。
pip install gym[classic_control]pip install pyglet
# Install additional packages for visualizationsudo apt-get install -y python-opengl > /dev/null 2>&1pip install git+https://github.com/tensorflow/docs > /dev/null 2>&1
import collections
import gym
import numpy as np
import statistics
import tensorflow as tf
import tqdm
from matplotlib import pyplot as plt
from tensorflow.keras import layers
from typing import Any, List, Sequence, Tuple
# Create the environment
env = gym.make("CartPole-v1")
# Set seed for experiment reproducibility
seed = 42
tf.random.set_seed(seed)
np.random.seed(seed)
# Small epsilon value for stabilizing division operations
eps = np.finfo(np.float32).eps.item()
模型
Actor 和 Critic 将使用一个神经网络来建模,该神经网络分别生成动作概率和 Critic 价值。本教程使用模型子类化来定义模型。
在正向传播过程中,模型将以状态作为输入,并输出动作概率和 Critic 价值 \(V\),它模拟了依赖于状态的 价值函数。目标是训练一个模型,该模型根据策略 \(\pi\) 选择动作,该策略最大化预期 回报。
对于 CartPole-v0,有四个值代表状态:小车位置、小车速度、杆子角度和杆子速度。代理可以采取两个动作来推动小车向左 (0) 和向右 (1)。
有关更多信息,请参阅 Gym 的 Cart Pole 文档页面 和 可以解决困难学习控制问题的类神经自适应元素,作者为 Barto、Sutton 和 Anderson (1983)。
class ActorCritic(tf.keras.Model):
"""Combined actor-critic network."""
def __init__(
self,
num_actions: int,
num_hidden_units: int):
"""Initialize."""
super().__init__()
self.common = layers.Dense(num_hidden_units, activation="relu")
self.actor = layers.Dense(num_actions)
self.critic = layers.Dense(1)
def call(self, inputs: tf.Tensor) -> Tuple[tf.Tensor, tf.Tensor]:
x = self.common(inputs)
return self.actor(x), self.critic(x)
num_actions = env.action_space.n # 2
num_hidden_units = 128
model = ActorCritic(num_actions, num_hidden_units)
训练代理
要训练代理,您将按照以下步骤进行
- 在环境上运行代理以收集每集的训练数据。
- 计算每个时间步长的预期回报。
- 计算组合 Actor-Critic 模型的损失。
- 计算梯度并更新网络参数。
- 重复 1-4,直到成功标准或最大集数达到为止。
1. 收集训练数据
与监督学习一样,为了训练 Actor-Critic 模型,您需要有训练数据。但是,为了收集此类数据,模型需要在环境中“运行”。
每集收集训练数据。然后,在每个时间步长,模型的正向传播将在环境的状态上运行,以根据当前策略(由模型的权重参数化)生成动作概率和 Critic 价值。
下一个动作将从模型生成的动作概率中采样,然后应用于环境,从而生成下一个状态和奖励。
此过程在 run_episode 函数中实现,该函数使用 TensorFlow 操作,以便它可以稍后被编译成 TensorFlow 图以进行更快的训练。请注意,tf.TensorArray 用于支持可变长度数组上的张量迭代。
# Wrap Gym's `env.step` call as an operation in a TensorFlow function.
# This would allow it to be included in a callable TensorFlow graph.
@tf.numpy_function(Tout=[tf.float32, tf.int32, tf.int32])
def env_step(action: np.ndarray) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
"""Returns state, reward and done flag given an action."""
state, reward, done, truncated, info = env.step(action)
return (state.astype(np.float32),
np.array(reward, np.int32),
np.array(done, np.int32))
def run_episode(
initial_state: tf.Tensor,
model: tf.keras.Model,
max_steps: int) -> Tuple[tf.Tensor, tf.Tensor, tf.Tensor]:
"""Runs a single episode to collect training data."""
action_probs = tf.TensorArray(dtype=tf.float32, size=0, dynamic_size=True)
values = tf.TensorArray(dtype=tf.float32, size=0, dynamic_size=True)
rewards = tf.TensorArray(dtype=tf.int32, size=0, dynamic_size=True)
initial_state_shape = initial_state.shape
state = initial_state
for t in tf.range(max_steps):
# Convert state into a batched tensor (batch size = 1)
state = tf.expand_dims(state, 0)
# Run the model and to get action probabilities and critic value
action_logits_t, value = model(state)
# Sample next action from the action probability distribution
action = tf.random.categorical(action_logits_t, 1)[0, 0]
action_probs_t = tf.nn.softmax(action_logits_t)
# Store critic values
values = values.write(t, tf.squeeze(value))
# Store log probability of the action chosen
action_probs = action_probs.write(t, action_probs_t[0, action])
# Apply action to the environment to get next state and reward
state, reward, done = env_step(action)
state.set_shape(initial_state_shape)
# Store reward
rewards = rewards.write(t, reward)
if tf.cast(done, tf.bool):
break
action_probs = action_probs.stack()
values = values.stack()
rewards = rewards.stack()
return action_probs, values, rewards
2. 计算预期回报
在一集期间收集的每个时间步长 \(t\) 的奖励序列 \(\{r_{t}\}^{T}_{t=1}\) 被转换为预期回报序列 \(\{G_{t}\}^{T}_{t=1}\),其中奖励的总和是从当前时间步长 \(t\) 到 \(T\) 取的,并且每个奖励都乘以指数衰减的折扣因子 \(\gamma\)
\[G_{t} = \sum^{T}_{t'=t} \gamma^{t'-t}r_{t'}\]
由于 \(\gamma\in(0,1)\),因此距离当前时间步长更远的奖励的权重更低。
直观地说,预期回报仅仅意味着现在的奖励比以后的奖励更好。从数学意义上讲,它是为了确保奖励的总和收敛。
为了稳定训练,得到的回报序列也进行了标准化(即具有零均值和单位标准差)。
def get_expected_return(
rewards: tf.Tensor,
gamma: float,
standardize: bool = True) -> tf.Tensor:
"""Compute expected returns per timestep."""
n = tf.shape(rewards)[0]
returns = tf.TensorArray(dtype=tf.float32, size=n)
# Start from the end of `rewards` and accumulate reward sums
# into the `returns` array
rewards = tf.cast(rewards[::-1], dtype=tf.float32)
discounted_sum = tf.constant(0.0)
discounted_sum_shape = discounted_sum.shape
for i in tf.range(n):
reward = rewards[i]
discounted_sum = reward + gamma * discounted_sum
discounted_sum.set_shape(discounted_sum_shape)
returns = returns.write(i, discounted_sum)
returns = returns.stack()[::-1]
if standardize:
returns = ((returns - tf.math.reduce_mean(returns)) /
(tf.math.reduce_std(returns) + eps))
return returns
3. Actor-Critic 损失
由于您使用的是混合 Actor-Critic 模型,因此所选的损失函数是 Actor 和 Critic 损失的组合,用于训练,如下所示
\[L = L_{actor} + L_{critic}\]
Actor 损失
Actor 损失基于 使用 Critic 作为状态相关基线的策略梯度,并使用单样本(每集)估计进行计算。
\[L_{actor} = -\sum^{T}_{t=1} \log\pi_{\theta}(a_{t} | s_{t})[G(s_{t}, a_{t}) - V^{\pi}_{\theta}(s_{t})]\]
其中
- \(T\):每集的时间步长数,每集可能不同
- \(s_{t}\):时间步长 \(t\) 的状态
- \(a_{t}\):给定状态 \(s\) 时,在时间步长 \(t\) 选择的动作
- \(\pi_{\theta}\):由 \(\theta\) 参数化的策略(Actor)
- \(V^{\pi}_{\theta}\):也是由 \(\theta\) 参数化的价值函数(Critic)
- \(G = G_{t}\):给定状态、动作对在时间步长 \(t\) 的预期回报
在总和中添加了一个负项,因为想法是通过最小化组合损失来最大化产生更高奖励的动作的概率。
优势
\(L_{actor}\) 公式中的 \(G - V\) 项称为 优势,它表示给定特定状态的动作比根据该状态的策略 \(\pi\) 随机选择的动作好多少。
虽然可以排除基线,但这可能会导致训练期间出现高方差。选择 Critic \(V\) 作为基线的优点是,它经过训练尽可能接近 \(G\),从而导致方差更低。
此外,如果没有 Critic,算法将尝试根据预期回报来增加对特定状态下采取的动作的概率,如果动作之间的相对概率保持不变,这可能不会有太大区别。
例如,假设给定状态的两个动作将产生相同的预期回报。如果没有 Critic,算法将尝试根据目标 \(J\) 提高这些动作的概率。使用 Critic,结果可能表明没有优势 (\(G - V = 0\)),因此增加动作概率不会带来任何好处,算法将把梯度设置为零。
Critic 损失
训练 \(V\) 使其尽可能接近 \(G\) 可以设置为一个回归问题,使用以下损失函数
\[L_{critic} = L_{\delta}(G, V^{\pi}_{\theta})\]
其中 \(L_{\delta}\) 是 Huber 损失,它对数据中的异常值比平方误差损失更不敏感。
huber_loss = tf.keras.losses.Huber(reduction=tf.keras.losses.Reduction.SUM)
def compute_loss(
action_probs: tf.Tensor,
values: tf.Tensor,
returns: tf.Tensor) -> tf.Tensor:
"""Computes the combined Actor-Critic loss."""
advantage = returns - values
action_log_probs = tf.math.log(action_probs)
actor_loss = -tf.math.reduce_sum(action_log_probs * advantage)
critic_loss = huber_loss(values, returns)
return actor_loss + critic_loss
4. 定义训练步骤以更新参数
以上所有步骤都组合成一个训练步骤,该步骤在每集运行一次。所有导致损失函数的步骤都使用 tf.GradientTape 上下文执行,以启用自动微分。
本教程使用 Adam 优化器将梯度应用于模型参数。
未折现奖励的总和 episode_reward 也在此步骤中计算。此值将在稍后用于评估是否满足成功标准。
tf.function 上下文应用于 train_step 函数,以便它可以被编译成可调用的 TensorFlow 图,这可以导致训练速度提高 10 倍。
optimizer = tf.keras.optimizers.Adam(learning_rate=0.01)
@tf.function
def train_step(
initial_state: tf.Tensor,
model: tf.keras.Model,
optimizer: tf.keras.optimizers.Optimizer,
gamma: float,
max_steps_per_episode: int) -> tf.Tensor:
"""Runs a model training step."""
with tf.GradientTape() as tape:
# Run the model for one episode to collect training data
action_probs, values, rewards = run_episode(
initial_state, model, max_steps_per_episode)
# Calculate the expected returns
returns = get_expected_return(rewards, gamma)
# Convert training data to appropriate TF tensor shapes
action_probs, values, returns = [
tf.expand_dims(x, 1) for x in [action_probs, values, returns]]
# Calculate the loss values to update our network
loss = compute_loss(action_probs, values, returns)
# Compute the gradients from the loss
grads = tape.gradient(loss, model.trainable_variables)
# Apply the gradients to the model's parameters
optimizer.apply_gradients(zip(grads, model.trainable_variables))
episode_reward = tf.math.reduce_sum(rewards)
return episode_reward
5. 运行训练循环
训练通过运行训练步骤来执行,直到成功标准或最大集数达到为止。
在队列中保留一集奖励的运行记录。达到 100 次试验后,最旧的奖励将从队列的左侧(尾部)移除,最新的奖励将添加到头部(右侧)。为了提高计算效率,还维护奖励的运行总和。
根据您的运行时,训练可以在不到一分钟的时间内完成。
%%time
min_episodes_criterion = 100
max_episodes = 10000
max_steps_per_episode = 500
# `CartPole-v1` is considered solved if average reward is >= 475 over 500
# consecutive trials
reward_threshold = 475
running_reward = 0
# The discount factor for future rewards
gamma = 0.99
# Keep the last episodes reward
episodes_reward: collections.deque = collections.deque(maxlen=min_episodes_criterion)
t = tqdm.trange(max_episodes)
for i in t:
initial_state, info = env.reset()
initial_state = tf.constant(initial_state, dtype=tf.float32)
episode_reward = int(train_step(
initial_state, model, optimizer, gamma, max_steps_per_episode))
episodes_reward.append(episode_reward)
running_reward = statistics.mean(episodes_reward)
t.set_postfix(
episode_reward=episode_reward, running_reward=running_reward)
# Show the average episode reward every 10 episodes
if i % 10 == 0:
pass # print(f'Episode {i}: average reward: {avg_reward}')
if running_reward > reward_threshold and i >= min_episodes_criterion:
break
print(f'\nSolved at episode {i}: average reward: {running_reward:.2f}!')
0%| | 0/10000 [00:00<?, ?it/s]/tmpfs/src/tf_docs_env/lib/python3.9/site-packages/gym/utils/passive_env_checker.py:233: DeprecationWarning: `np.bool8` is a deprecated alias for `np.bool_`. (Deprecated NumPy 1.24) if not isinstance(terminated, (bool, np.bool8)): 11%|█▏ | 1138/10000 [03:54<30:29, 4.84it/s, episode_reward=500, running_reward=475] Solved at episode 1138: average reward: 475.13! CPU times: user 8min 21s, sys: 1min 20s, total: 9min 41s Wall time: 3min 54s
可视化
训练后,最好可视化模型在环境中的表现。您可以运行下面的单元格以生成模型运行一集的 GIF 动画。请注意,需要安装其他包才能使 Gym 正确地渲染环境的图像,以便在 Colab 中使用。
# Render an episode and save as a GIF file
from IPython import display as ipythondisplay
from PIL import Image
render_env = gym.make("CartPole-v1", render_mode='rgb_array')
def render_episode(env: gym.Env, model: tf.keras.Model, max_steps: int):
state, info = env.reset()
state = tf.constant(state, dtype=tf.float32)
screen = env.render()
images = [Image.fromarray(screen)]
for i in range(1, max_steps + 1):
state = tf.expand_dims(state, 0)
action_probs, _ = model(state)
action = np.argmax(np.squeeze(action_probs))
state, reward, done, truncated, info = env.step(action)
state = tf.constant(state, dtype=tf.float32)
# Render screen every 10 steps
if i % 10 == 0:
screen = env.render()
images.append(Image.fromarray(screen))
if done:
break
return images
# Save GIF image
images = render_episode(render_env, model, max_steps_per_episode)
image_file = 'cartpole-v1.gif'
# loop=0: loop forever, duration=1: play each frame for 1ms
images[0].save(
image_file, save_all=True, append_images=images[1:], loop=0, duration=1)
import tensorflow_docs.vis.embed as embed
embed.embed_file(image_file)
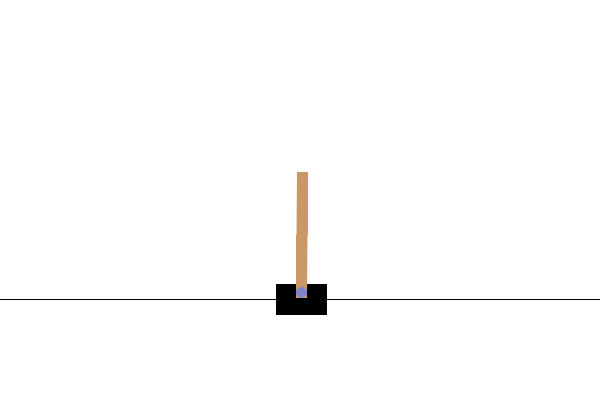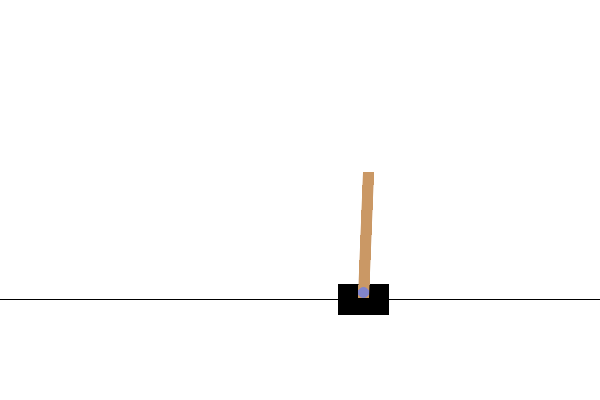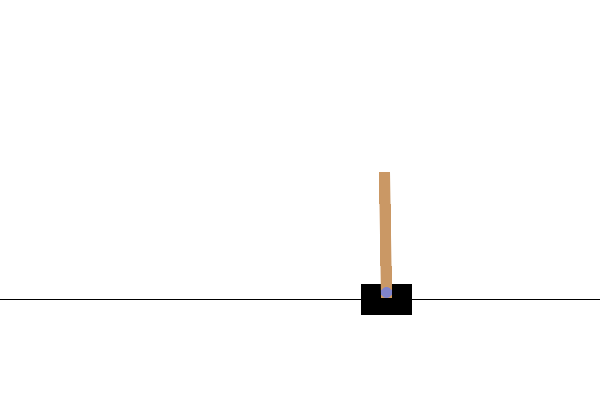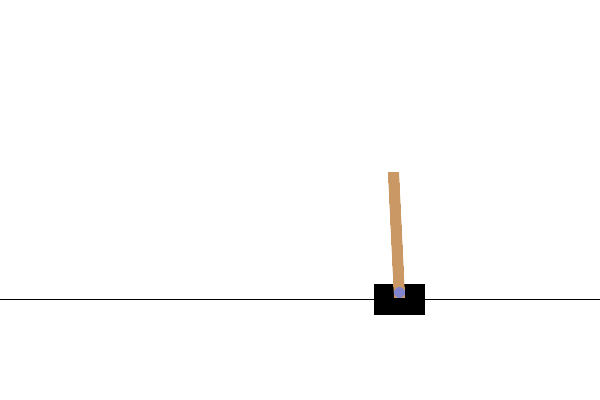
后续步骤
本教程演示了如何使用 Tensorflow 实现 Actor-Critic 方法。
下一步,您可以尝试在 Gym 中的另一个环境上训练模型。
有关 Actor-Critic 方法和 Cartpole-v0 问题的更多信息,您可以参考以下资源
有关 TensorFlow 中更多强化学习示例,您可以查看以下资源
