 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看 在 GitHub 上查看
|
 下载笔记本 下载笔记本
|
欢迎使用 **TensorFlow 决策森林** (**TF-DF**) 的 **排序学习 Colab**。在这个 Colab 中,您将学习如何使用 **TF-DF** 进行排序。
此 Colab 假设您熟悉 初学者 Colab 中介绍的概念,特别是关于 TF-DF 的安装。
在这个 Colab 中,您将
- 了解什么是排序模型。
- 在 LETOR3 数据集上训练梯度提升树模型。
- 评估此模型的质量。
安装 TensorFlow 决策森林
通过运行以下单元格来安装 TF-DF。
pip install tensorflow_decision_forests
Wurlitzer 是在 Colab 中显示详细训练日志(在模型构造函数中使用 verbose=2 时)所需的。
pip install wurlitzer
导入库
import os
# Keep using Keras 2
os.environ['TF_USE_LEGACY_KERAS'] = '1'
import tensorflow_decision_forests as tfdf
import numpy as np
import pandas as pd
import tensorflow as tf
import tf_keras
import math
隐藏的代码单元格限制了 Colab 中的输出高度。
# Check the version of TensorFlow Decision Forests
print("Found TensorFlow Decision Forests v" + tfdf.__version__)
Found TensorFlow Decision Forests v1.9.0
什么是排序模型?
排序模型的目标是 **正确排序** 项目。例如,排序可用于在用户 **查询** 后选择要检索的最佳 **文档**。
表示排序数据集的一种常见方法是使用“相关性”分数:元素的顺序由其相关性定义:相关性更高的项目应位于相关性更低的项目之前。错误的成本由预测项目与正确项目的相关性之差定义。例如,对相关性分别为 3 和 4 的两个项目进行错误排序,并不像对相关性分别为 1 和 5 的两个项目进行错误排序那样糟糕。
TF-DF 期望排序数据集以“扁平”格式呈现。查询和相应文档的数据集可能如下所示
| 查询 | 文档 ID | 特征 1 | 特征 2 | 相关性 |
|---|---|---|---|---|
| 猫 | 1 | 0.1 | 蓝色 | 4 |
| 猫 | 2 | 0.5 | 绿色 | 1 |
| 猫 | 3 | 0.2 | 红色 | 2 |
| 狗 | 4 | NA | 红色 | 0 |
| 狗 | 5 | 0.2 | 红色 | 0 |
| 狗 | 6 | 0.6 | 绿色 | 1 |
相关性/标签 是一个介于 0 到 5 之间的浮点数值(通常介于 0 到 4 之间),其中 0 表示“完全不相关”,4 表示“非常相关”,5 表示“与查询相同”。
在此示例中,文档 1 与查询“猫”非常相关,而文档 2 仅与猫“相关”。没有文档真正谈论“狗”(文档 6 的最高相关性为 1)。但是,狗查询仍然期望返回文档 6(因为这是最“多”谈论狗的文档)。
有趣的是,决策森林通常是优秀的排序器,许多最先进的排序模型都是决策森林。
让我们训练一个排序模型
在此示例中,使用 LETOR3 数据集的样本。更准确地说,我们想要从 LETOR3 仓库 下载 OHSUMED.zip。此数据集以 libsvm 格式存储,因此我们需要将其转换为 csv。
archive_path = tf_keras.utils.get_file("letor.zip",
"https://download.microsoft.com/download/E/7/E/E7EABEF1-4C7B-4E31-ACE5-73927950ED5E/Letor.zip",
extract=True)
# Path to a ranking ataset using libsvm format.
raw_dataset_path = os.path.join(os.path.dirname(archive_path),"OHSUMED/Data/Fold1/trainingset.txt")
Downloading data from https://download.microsoft.com/download/E/7/E/E7EABEF1-4C7B-4E31-ACE5-73927950ED5E/Letor.zip 61824018/61824018 [==============================] - 7s 0us/step
以下是数据集的前几行
head {raw_dataset_path}
第一步是将此数据集转换为上面提到的“扁平”格式。
def convert_libsvm_to_csv(src_path, dst_path):
"""Converts a libsvm ranking dataset into a flat csv file.
Note: This code is specific to the LETOR3 dataset.
"""
dst_handle = open(dst_path, "w")
first_line = True
for src_line in open(src_path,"r"):
# Note: The last 3 items are comments.
items = src_line.split(" ")[:-3]
relevance = items[0]
group = items[1].split(":")[1]
features = [ item.split(":") for item in items[2:]]
if first_line:
# Csv header
dst_handle.write("relevance,group," + ",".join(["f_" + feature[0] for feature in features]) + "\n")
first_line = False
dst_handle.write(relevance + ",g_" + group + "," + (",".join([feature[1] for feature in features])) + "\n")
dst_handle.close()
# Convert the dataset.
csv_dataset_path="/tmp/ohsumed.csv"
convert_libsvm_to_csv(raw_dataset_path, csv_dataset_path)
# Load a dataset into a Pandas Dataframe.
dataset_df = pd.read_csv(csv_dataset_path)
# Display the first 3 examples.
dataset_df.head(3)
在此数据集中,每行代表一个查询/文档对(称为“组”)。“相关性”表示查询与文档匹配的程度。
查询和文档的特征在“f1-25”中合并在一起。特征的确切定义未知,但它可能类似于
- 查询中的单词数
- 查询和文档之间共同单词的数量
- 查询嵌入与文档嵌入之间的余弦相似度。
- ...
让我们将 Pandas 数据帧转换为 TensorFlow 数据集
dataset_ds = tfdf.keras.pd_dataframe_to_tf_dataset(dataset_df, label="relevance", task=tfdf.keras.Task.RANKING)
让我们配置和训练我们的排序模型。
%set_cell_height 400
model = tfdf.keras.GradientBoostedTreesModel(
task=tfdf.keras.Task.RANKING,
ranking_group="group",
num_trees=50)
model.fit(dataset_ds)
<IPython.core.display.Javascript object> Warning: The `num_threads` constructor argument is not set and the number of CPU is os.cpu_count()=32 > 32. Setting num_threads to 32. Set num_threads manually to use more than 32 cpus. WARNING:absl:The `num_threads` constructor argument is not set and the number of CPU is os.cpu_count()=32 > 32. Setting num_threads to 32. Set num_threads manually to use more than 32 cpus. Use /tmpfs/tmp/tmpzqjjgty3 as temporary training directory Reading training dataset... [WARNING 24-04-20 11:09:14.5069 UTC gradient_boosted_trees.cc:1840] "goss_alpha" set but "sampling_method" not equal to "GOSS". [WARNING 24-04-20 11:09:14.5069 UTC gradient_boosted_trees.cc:1851] "goss_beta" set but "sampling_method" not equal to "GOSS". [WARNING 24-04-20 11:09:14.5069 UTC gradient_boosted_trees.cc:1865] "selective_gradient_boosting_ratio" set but "sampling_method" not equal to "SELGB". Training dataset read in 0:00:03.986733. Found 9219 examples. Training model... Model trained in 0:00:00.757738 Compiling model... [INFO 24-04-20 11:09:19.2736 UTC kernel.cc:1233] Loading model from path /tmpfs/tmp/tmpzqjjgty3/model/ with prefix fa7585ffd7c24e56 [INFO 24-04-20 11:09:19.2748 UTC quick_scorer_extended.cc:911] The binary was compiled without AVX2 support, but your CPU supports it. Enable it for faster model inference. [INFO 24-04-20 11:09:19.2749 UTC abstract_model.cc:1344] Engine "GradientBoostedTreesQuickScorerExtended" built [INFO 24-04-20 11:09:19.2749 UTC kernel.cc:1061] Use fast generic engine Model compiled. <tf_keras.src.callbacks.History at 0x7fb6979cc8b0>
现在我们可以查看模型在验证数据集上的质量。默认情况下,TF-DF 训练排序模型以优化 NDCG。NDCG 是一个介于 0 到 1 之间的数值,其中 1 是完美分数。因此,-NDCG 是模型损失。
import matplotlib.pyplot as plt
logs = model.make_inspector().training_logs()
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot([log.num_trees for log in logs], [log.evaluation.ndcg for log in logs])
plt.xlabel("Number of trees")
plt.ylabel("NDCG (validation)")
plt.subplot(1, 2, 2)
plt.plot([log.num_trees for log in logs], [log.evaluation.loss for log in logs])
plt.xlabel("Number of trees")
plt.ylabel("Loss (validation)")
plt.show()
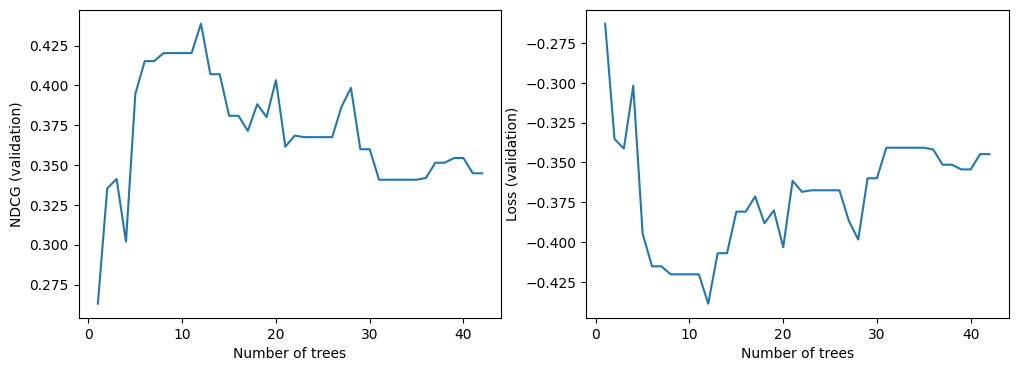
与所有 TF-DF 模型一样,您也可以查看模型报告(注意:模型报告还包含训练日志)
%set_cell_height 400
model.summary()
<IPython.core.display.Javascript object>
Model: "gradient_boosted_trees_model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
=================================================================
Total params: 1 (1.00 Byte)
Trainable params: 0 (0.00 Byte)
Non-trainable params: 1 (1.00 Byte)
_________________________________________________________________
Type: "GRADIENT_BOOSTED_TREES"
Task: RANKING
Label: "__LABEL"
Rank group: "group"
Input Features (25):
f_1
f_10
f_11
f_12
f_13
f_14
f_15
f_16
f_17
f_18
f_19
f_2
f_20
f_21
f_22
f_23
f_24
f_25
f_3
f_4
f_5
f_6
f_7
f_8
f_9
No weights
Variable Importance: INV_MEAN_MIN_DEPTH:
1. "f_9" 0.326164 ################
2. "f_3" 0.318071 ###############
3. "f_8" 0.308922 #############
4. "f_4" 0.271175 #########
5. "f_19" 0.221570 ###
6. "f_10" 0.215666 ##
7. "f_11" 0.206509 #
8. "f_22" 0.204742 #
9. "f_25" 0.204497 #
10. "f_23" 0.203238
11. "f_21" 0.200830
12. "f_24" 0.200445
13. "f_12" 0.198840
14. "f_18" 0.197676
15. "f_20" 0.196634
16. "f_6" 0.196085
17. "f_16" 0.196061
18. "f_2" 0.195683
19. "f_5" 0.195683
20. "f_13" 0.195559
21. "f_17" 0.195559
Variable Importance: NUM_AS_ROOT:
1. "f_3" 4.000000 ################
2. "f_4" 4.000000 ################
3. "f_8" 3.000000 ##########
4. "f_9" 1.000000
Variable Importance: NUM_NODES:
1. "f_8" 25.000000 ################
2. "f_19" 18.000000 ###########
3. "f_10" 15.000000 #########
4. "f_9" 14.000000 ########
5. "f_3" 13.000000 ########
6. "f_23" 7.000000 ####
7. "f_24" 6.000000 ###
8. "f_11" 5.000000 ##
9. "f_21" 5.000000 ##
10. "f_25" 5.000000 ##
11. "f_4" 5.000000 ##
12. "f_22" 4.000000 ##
13. "f_12" 3.000000 #
14. "f_20" 3.000000 #
15. "f_16" 2.000000
16. "f_6" 2.000000
17. "f_13" 1.000000
18. "f_17" 1.000000
19. "f_18" 1.000000
20. "f_2" 1.000000
21. "f_5" 1.000000
Variable Importance: SUM_SCORE:
1. "f_8" 10779.340861 ################
2. "f_9" 8831.772410 #############
3. "f_3" 4526.101184 ######
4. "f_4" 4360.245403 ######
5. "f_19" 2325.288894 ###
6. "f_10" 1881.848369 ##
7. "f_21" 1674.980191 ##
8. "f_11" 1127.632256 #
9. "f_23" 1021.834252 #
10. "f_24" 914.851512 #
11. "f_22" 885.619576 #
12. "f_25" 748.665007 #
13. "f_20" 310.610858
14. "f_16" 298.972842
15. "f_6" 212.376573
16. "f_12" 130.725240
17. "f_2" 112.124991
18. "f_18" 86.341193
19. "f_5" 65.103908
20. "f_13" 57.966947
21. "f_17" 21.930388
Loss: LAMBDA_MART_NDCG5
Validation loss value: -0.438692
Number of trees per iteration: 1
Node format: NOT_SET
Number of trees: 12
Total number of nodes: 286
Number of nodes by tree:
Count: 12 Average: 23.8333 StdDev: 3.50793
Min: 17 Max: 29 Ignored: 0
----------------------------------------------
[ 17, 18) 1 8.33% 8.33% ###
[ 18, 19) 0 0.00% 8.33%
[ 19, 20) 1 8.33% 16.67% ###
[ 20, 21) 0 0.00% 16.67%
[ 21, 22) 2 16.67% 33.33% #######
[ 22, 23) 0 0.00% 33.33%
[ 23, 24) 1 8.33% 41.67% ###
[ 24, 25) 0 0.00% 41.67%
[ 25, 26) 3 25.00% 66.67% ##########
[ 26, 27) 0 0.00% 66.67%
[ 27, 28) 3 25.00% 91.67% ##########
[ 28, 29) 0 0.00% 91.67%
[ 29, 29] 1 8.33% 100.00% ###
Depth by leafs:
Count: 149 Average: 4.14094 StdDev: 1.08696
Min: 1 Max: 5 Ignored: 0
----------------------------------------------
[ 1, 2) 2 1.34% 1.34%
[ 2, 3) 18 12.08% 13.42% ##
[ 3, 4) 13 8.72% 22.15% ##
[ 4, 5) 40 26.85% 48.99% #####
[ 5, 5] 76 51.01% 100.00% ##########
Number of training obs by leaf:
Count: 149 Average: 673.691 StdDev: 2015.44
Min: 5 Max: 8211 Ignored: 0
----------------------------------------------
[ 5, 415) 127 85.23% 85.23% ##########
[ 415, 825) 6 4.03% 89.26%
[ 825, 1236) 2 1.34% 90.60%
[ 1236, 1646) 0 0.00% 90.60%
[ 1646, 2056) 0 0.00% 90.60%
[ 2056, 2467) 1 0.67% 91.28%
[ 2467, 2877) 0 0.00% 91.28%
[ 2877, 3287) 0 0.00% 91.28%
[ 3287, 3698) 1 0.67% 91.95%
[ 3698, 4108) 0 0.00% 91.95%
[ 4108, 4518) 0 0.00% 91.95%
[ 4518, 4929) 1 0.67% 92.62%
[ 4929, 5339) 0 0.00% 92.62%
[ 5339, 5749) 0 0.00% 92.62%
[ 5749, 6160) 1 0.67% 93.29%
[ 6160, 6570) 0 0.00% 93.29%
[ 6570, 6980) 0 0.00% 93.29%
[ 6980, 7391) 0 0.00% 93.29%
[ 7391, 7801) 8 5.37% 98.66% #
[ 7801, 8211] 2 1.34% 100.00%
Attribute in nodes:
25 : f_8 [NUMERICAL]
18 : f_19 [NUMERICAL]
15 : f_10 [NUMERICAL]
14 : f_9 [NUMERICAL]
13 : f_3 [NUMERICAL]
7 : f_23 [NUMERICAL]
6 : f_24 [NUMERICAL]
5 : f_4 [NUMERICAL]
5 : f_25 [NUMERICAL]
5 : f_21 [NUMERICAL]
5 : f_11 [NUMERICAL]
4 : f_22 [NUMERICAL]
3 : f_20 [NUMERICAL]
3 : f_12 [NUMERICAL]
2 : f_6 [NUMERICAL]
2 : f_16 [NUMERICAL]
1 : f_5 [NUMERICAL]
1 : f_2 [NUMERICAL]
1 : f_18 [NUMERICAL]
1 : f_17 [NUMERICAL]
1 : f_13 [NUMERICAL]
Attribute in nodes with depth <= 0:
4 : f_4 [NUMERICAL]
4 : f_3 [NUMERICAL]
3 : f_8 [NUMERICAL]
1 : f_9 [NUMERICAL]
Attribute in nodes with depth <= 1:
11 : f_9 [NUMERICAL]
9 : f_8 [NUMERICAL]
4 : f_4 [NUMERICAL]
4 : f_3 [NUMERICAL]
1 : f_25 [NUMERICAL]
1 : f_24 [NUMERICAL]
1 : f_23 [NUMERICAL]
1 : f_22 [NUMERICAL]
1 : f_19 [NUMERICAL]
1 : f_11 [NUMERICAL]
Attribute in nodes with depth <= 2:
15 : f_8 [NUMERICAL]
12 : f_9 [NUMERICAL]
11 : f_3 [NUMERICAL]
6 : f_19 [NUMERICAL]
5 : f_4 [NUMERICAL]
2 : f_25 [NUMERICAL]
2 : f_11 [NUMERICAL]
2 : f_10 [NUMERICAL]
1 : f_24 [NUMERICAL]
1 : f_23 [NUMERICAL]
1 : f_22 [NUMERICAL]
1 : f_18 [NUMERICAL]
1 : f_17 [NUMERICAL]
Attribute in nodes with depth <= 3:
22 : f_8 [NUMERICAL]
13 : f_9 [NUMERICAL]
11 : f_3 [NUMERICAL]
10 : f_19 [NUMERICAL]
9 : f_10 [NUMERICAL]
5 : f_4 [NUMERICAL]
5 : f_23 [NUMERICAL]
5 : f_11 [NUMERICAL]
4 : f_25 [NUMERICAL]
4 : f_22 [NUMERICAL]
4 : f_21 [NUMERICAL]
3 : f_24 [NUMERICAL]
2 : f_12 [NUMERICAL]
1 : f_18 [NUMERICAL]
1 : f_17 [NUMERICAL]
Attribute in nodes with depth <= 5:
25 : f_8 [NUMERICAL]
18 : f_19 [NUMERICAL]
15 : f_10 [NUMERICAL]
14 : f_9 [NUMERICAL]
13 : f_3 [NUMERICAL]
7 : f_23 [NUMERICAL]
6 : f_24 [NUMERICAL]
5 : f_4 [NUMERICAL]
5 : f_25 [NUMERICAL]
5 : f_21 [NUMERICAL]
5 : f_11 [NUMERICAL]
4 : f_22 [NUMERICAL]
3 : f_20 [NUMERICAL]
3 : f_12 [NUMERICAL]
2 : f_6 [NUMERICAL]
2 : f_16 [NUMERICAL]
1 : f_5 [NUMERICAL]
1 : f_2 [NUMERICAL]
1 : f_18 [NUMERICAL]
1 : f_17 [NUMERICAL]
1 : f_13 [NUMERICAL]
Condition type in nodes:
137 : HigherCondition
Condition type in nodes with depth <= 0:
12 : HigherCondition
Condition type in nodes with depth <= 1:
34 : HigherCondition
Condition type in nodes with depth <= 2:
60 : HigherCondition
Condition type in nodes with depth <= 3:
99 : HigherCondition
Condition type in nodes with depth <= 5:
137 : HigherCondition
Training logs:
Number of iteration to final model: 12
Iter:1 train-loss:-0.346669 valid-loss:-0.262935 train-NDCG@5:0.346669 valid-NDCG@5:0.262935
Iter:2 train-loss:-0.412635 valid-loss:-0.335301 train-NDCG@5:0.412635 valid-NDCG@5:0.335301
Iter:3 train-loss:-0.468270 valid-loss:-0.341295 train-NDCG@5:0.468270 valid-NDCG@5:0.341295
Iter:4 train-loss:-0.481511 valid-loss:-0.301897 train-NDCG@5:0.481511 valid-NDCG@5:0.301897
Iter:5 train-loss:-0.473165 valid-loss:-0.394670 train-NDCG@5:0.473165 valid-NDCG@5:0.394670
Iter:6 train-loss:-0.496260 valid-loss:-0.415201 train-NDCG@5:0.496260 valid-NDCG@5:0.415201
Iter:16 train-loss:-0.526791 valid-loss:-0.380900 train-NDCG@5:0.526791 valid-NDCG@5:0.380900
Iter:26 train-loss:-0.560398 valid-loss:-0.367496 train-NDCG@5:0.560398 valid-NDCG@5:0.367496
Iter:36 train-loss:-0.584252 valid-loss:-0.341845 train-NDCG@5:0.584252 valid-NDCG@5:0.341845
如果您好奇,您也可以绘制模型
tfdf.model_plotter.plot_model_in_colab(model, tree_idx=0, max_depth=3)
使用排序模型进行预测
对于一个传入的查询,我们可以使用我们的排名模型来预测一组文档的相关性。在实践中,这意味着对于每个查询,我们必须找到一组可能与查询相关或不相关的文档。我们称这些文档为**候选文档**。对于每个查询/候选文档对,我们可以计算训练期间使用的相同特征。这就是我们的**服务数据集**。
回到本教程开头提到的例子,服务数据集可能看起来像这样
| 查询 | 文档 ID | 特征 1 | 特征 2 |
|---|---|---|---|
| 鱼 | 32 | 0.3 | 蓝色 |
| 鱼 | 33 | 1.0 | 绿色 |
| 鱼 | 34 | 0.4 | 蓝色 |
| 鱼 | 35 | NA | 棕色 |
请注意,相关性不属于服务数据集,因为这是模型试图预测的内容。
服务数据集被馈送到 TF-DF 模型,并为每个文档分配一个相关性分数。
| 查询 | 文档 ID | 特征 1 | 特征 2 | 相关性 |
|---|---|---|---|---|
| 鱼 | 32 | 0.3 | 蓝色 | 0.325 |
| 鱼 | 33 | 1.0 | 绿色 | 0.125 |
| 鱼 | 34 | 0.4 | 蓝色 | 0.155 |
| 鱼 | 35 | NA | 棕色 | 0.593 |
这意味着文档 ID 为 35 的文档被预测为与查询“鱼”最相关。
让我们尝试使用我们的真实模型来做到这一点。
# Path to a test dataset using libsvm format.
test_dataset_path = os.path.join(os.path.dirname(archive_path),"OHSUMED/Data/Fold1/testset.txt")
# Convert the dataset.
csv_test_dataset_path="/tmp/ohsumed_test.csv"
convert_libsvm_to_csv(raw_dataset_path, csv_test_dataset_path)
# Load a dataset into a Pandas Dataframe.
test_dataset_df = pd.read_csv(csv_test_dataset_path)
# Display the first 3 examples.
test_dataset_df.head(3)
假设我们的查询是“g_5”,并且测试数据集已经包含了此查询的候选文档。
# Filter by "g_5"
serving_dataset_df = test_dataset_df[test_dataset_df['group'] == 'g_5']
# Remove the columns for group and relevance, not needed for predictions.
serving_dataset_df = serving_dataset_df.drop(['relevance', 'group'], axis=1)
# Convert to a Tensorflow dataset
serving_dataset_ds = tfdf.keras.pd_dataframe_to_tf_dataset(serving_dataset_df, task=tfdf.keras.Task.RANKING)
# Run predictions with on all candidate documents
predictions = model.predict(serving_dataset_ds)
1/1 [==============================] - 0s 176ms/step
我们可以将预测添加到数据框中,并使用它们来查找得分最高的文档。
serving_dataset_df['prediction_score'] = predictions
serving_dataset_df.sort_values(by=['prediction_score'], ascending=False).head()
