 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
此笔记本使用 TensorFlow 核心低级 API 为手写数字分类构建端到端机器学习工作流程,使用 多层感知器 和 MNIST 数据集。访问 核心 API 概述 了解有关 TensorFlow 核心及其预期用例的更多信息。
多层感知器 (MLP) 概述
多层感知器 (MLP) 是一种前馈神经网络,用于解决 多类分类 问题。在构建 MLP 之前,了解感知器、层和激活函数的概念至关重要。
多层感知器由称为感知器的功能单元组成。感知器的方程如下
\[Z = \vec{w}⋅\mathrm{X} + b\]
其中
- \(Z\): 感知器输出
- \(\mathrm{X}\): 特征矩阵
- \(\vec{w}\): 权重向量
- \(b\): 偏差
当这些感知器堆叠在一起时,它们会形成称为密集层的结构,这些结构可以连接起来构建神经网络。密集层的方程类似于感知器的方程,但使用权重矩阵和偏差向量而不是
\[Z = \mathrm{W}⋅\mathrm{X} + \vec{b}\]
其中
- \(Z\): 密集层输出
- \(\mathrm{X}\): 特征矩阵
- \(\mathrm{W}\): 权重矩阵
- \(\vec{b}\): 偏差向量
在 MLP 中,多个密集层以一种方式连接,即一层输出完全连接到下一层的输入。在密集层输出中添加非线性激活函数可以帮助 MLP 分类器学习复杂的决策边界并很好地泛化到看不见的数据。
设置
导入 TensorFlow、pandas、Matplotlib 和 seaborn 开始。
# Use seaborn for countplot.pip install -q seaborn
import pandas as pd
import matplotlib
from matplotlib import pyplot as plt
import seaborn as sns
import tempfile
import os
# Preset Matplotlib figure sizes.
matplotlib.rcParams['figure.figsize'] = [9, 6]
import tensorflow as tf
import tensorflow_datasets as tfds
print(tf.__version__)
# Set random seed for reproducible results
tf.random.set_seed(22)
2023-10-04 01:27:29.112043: E tensorflow/compiler/xla/stream_executor/cuda/cuda_dnn.cc:9342] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2023-10-04 01:27:29.112093: E tensorflow/compiler/xla/stream_executor/cuda/cuda_fft.cc:609] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2023-10-04 01:27:29.112126: E tensorflow/compiler/xla/stream_executor/cuda/cuda_blas.cc:1518] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered 2.14.0
加载数据
本教程使用 MNIST 数据集,并演示如何构建可以对手写数字进行分类的 MLP 模型。该数据集可从 TensorFlow 数据集 获取。
将 MNIST 数据集拆分为训练集、验证集和测试集。验证集可用于在训练期间评估模型的泛化能力,以便测试集可以作为模型性能的最终无偏估计器。
train_data, val_data, test_data = tfds.load("mnist",
split=['train[10000:]', 'train[0:10000]', 'test'],
batch_size=128, as_supervised=True)
2023-10-04 01:27:32.380134: W tensorflow/core/common_runtime/gpu/gpu_device.cc:2211] Cannot dlopen some GPU libraries. Please make sure the missing libraries mentioned above are installed properly if you would like to use GPU. Follow the guide at https://tensorflowcn.cn/install/gpu for how to download and setup the required libraries for your platform. Skipping registering GPU devices...
MNIST 数据集包含手写数字及其相应的真实标签。在下面可视化几个示例。
x_viz, y_viz = tfds.load("mnist", split=['train[:1500]'], batch_size=-1, as_supervised=True)[0]
x_viz = tf.squeeze(x_viz, axis=3)
for i in range(9):
plt.subplot(3,3,1+i)
plt.axis('off')
plt.imshow(x_viz[i], cmap='gray')
plt.title(f"True Label: {y_viz[i]}")
plt.subplots_adjust(hspace=.5)

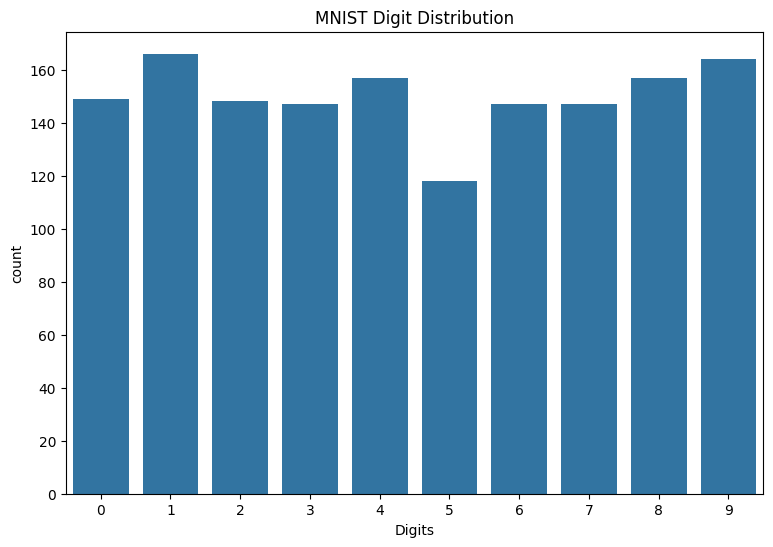
还可以查看训练数据中数字的分布,以验证每个类别在数据集中是否都有很好的表示。
sns.countplot(x=y_viz.numpy());
plt.xlabel('Digits')
plt.title("MNIST Digit Distribution");
预处理数据
首先,通过展平图像将特征矩阵重塑为二维。接下来,重新缩放数据,以便 [0,255] 的像素值适合 [0,1] 的范围。此步骤确保输入像素具有相似的分布,并有助于训练收敛。
def preprocess(x, y):
# Reshaping the data
x = tf.reshape(x, shape=[-1, 784])
# Rescaling the data
x = x/255
return x, y
train_data, val_data = train_data.map(preprocess), val_data.map(preprocess)
构建 MLP
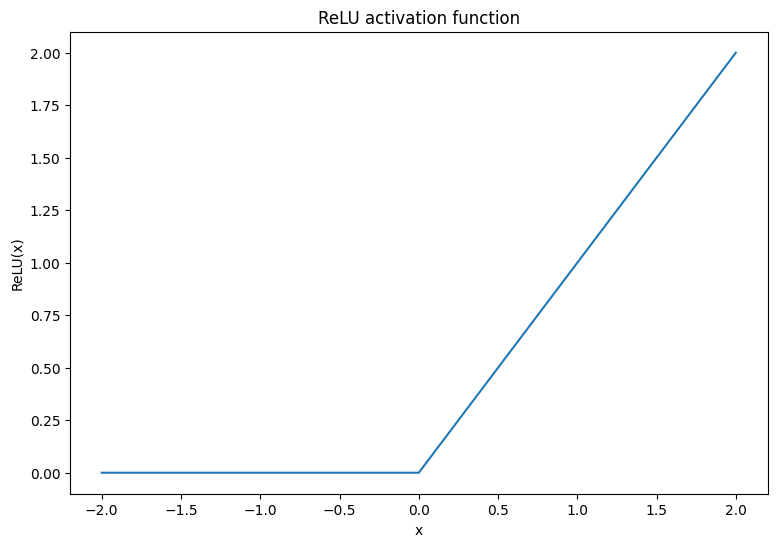
首先,让我们可视化一下 ReLU 和 Softmax 激活函数。这两个函数分别在 tf.nn.relu 和 tf.nn.softmax 中可用。ReLU 是一种非线性激活函数,当输入为正时输出输入值,否则输出 0。
\[\text{ReLU}(X) = max(0, X)\]
x = tf.linspace(-2, 2, 201)
x = tf.cast(x, tf.float32)
plt.plot(x, tf.nn.relu(x));
plt.xlabel('x')
plt.ylabel('ReLU(x)')
plt.title('ReLU activation function');
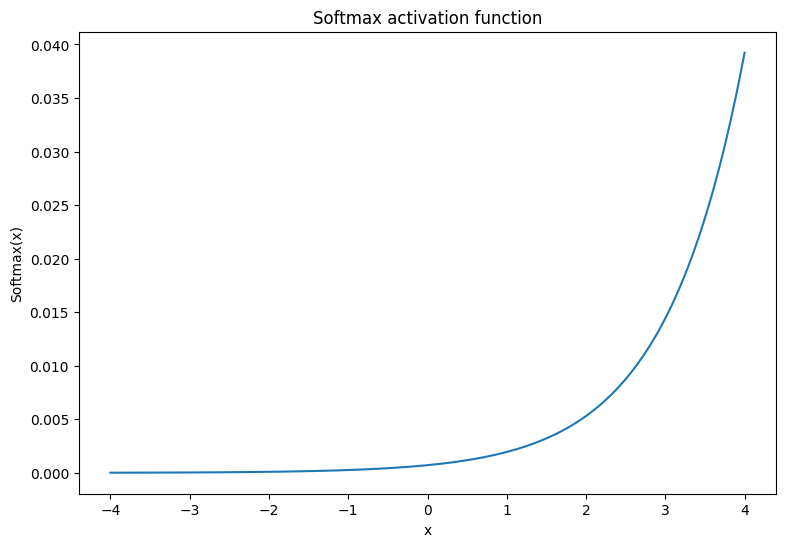
Softmax 激活函数是一个归一化的指数函数,它将 \(m\) 个实数转换为具有 \(m\) 个结果/类的概率分布。这对于从神经网络的输出预测类概率很有用。
\[\text{Softmax}(X) = \frac{e^{X} }{\sum_{i=1}^{m}e^{X_i} }\]
x = tf.linspace(-4, 4, 201)
x = tf.cast(x, tf.float32)
plt.plot(x, tf.nn.softmax(x, axis=0));
plt.xlabel('x')
plt.ylabel('Softmax(x)')
plt.title('Softmax activation function');
密集层
为密集层创建一个类。根据定义,MLP 中一层输出完全连接到下一层的输入。因此,密集层的输入维度可以根据其前一层的输出维度推断出来,并且在初始化时不需要预先指定。权重也应该被正确初始化,以防止激活输出变得过大或过小。最流行的权重初始化方法之一是 Xavier 方案,其中权重矩阵的每个元素都以以下方式采样
\[W_{ij} \sim \text{Uniform}(-\frac{\sqrt{6} }{\sqrt{n + m} },\frac{\sqrt{6} }{\sqrt{n + m} })\]
偏差向量可以初始化为零。
def xavier_init(shape):
# Computes the xavier initialization values for a weight matrix
in_dim, out_dim = shape
xavier_lim = tf.sqrt(6.)/tf.sqrt(tf.cast(in_dim + out_dim, tf.float32))
weight_vals = tf.random.uniform(shape=(in_dim, out_dim),
minval=-xavier_lim, maxval=xavier_lim, seed=22)
return weight_vals
Xavier 初始化方法也可以使用 tf.keras.initializers.GlorotUniform 实现。
class DenseLayer(tf.Module):
def __init__(self, out_dim, weight_init=xavier_init, activation=tf.identity):
# Initialize the dimensions and activation functions
self.out_dim = out_dim
self.weight_init = weight_init
self.activation = activation
self.built = False
def __call__(self, x):
if not self.built:
# Infer the input dimension based on first call
self.in_dim = x.shape[1]
# Initialize the weights and biases
self.w = tf.Variable(self.weight_init(shape=(self.in_dim, self.out_dim)))
self.b = tf.Variable(tf.zeros(shape=(self.out_dim,)))
self.built = True
# Compute the forward pass
z = tf.add(tf.matmul(x, self.w), self.b)
return self.activation(z)
接下来,构建一个用于 MLP 模型的类,该模型按顺序执行层。请记住,模型变量只有在第一次调用密集层序列后才可用,因为需要进行维度推断。
class MLP(tf.Module):
def __init__(self, layers):
self.layers = layers
@tf.function
def __call__(self, x, preds=False):
# Execute the model's layers sequentially
for layer in self.layers:
x = layer(x)
return x
使用以下架构初始化一个 MLP 模型
- 前向传播:ReLU(784 x 700) x ReLU(700 x 500) x Softmax(500 x 10)
Softmax 激活函数不需要由 MLP 应用。它在损失函数和预测函数中单独计算。
hidden_layer_1_size = 700
hidden_layer_2_size = 500
output_size = 10
mlp_model = MLP([
DenseLayer(out_dim=hidden_layer_1_size, activation=tf.nn.relu),
DenseLayer(out_dim=hidden_layer_2_size, activation=tf.nn.relu),
DenseLayer(out_dim=output_size)])
定义损失函数
交叉熵损失函数是多类分类问题的绝佳选择,因为它根据模型的概率预测来衡量数据的负对数似然。分配给真实类的概率越高,损失越低。交叉熵损失的公式如下
\[L = -\frac{1}{n}\sum_{i=1}^{n}\sum_{i=j}^{n} {y_j}^{[i]}⋅\log(\hat{ {y_j} }^{[i]})\]
其中
- \(\underset{n\times m}{\hat{y} }\): 预测类分布矩阵
- \(\underset{n\times m}{y}\): 真实类的独热编码矩阵
可以使用 tf.nn.sparse_softmax_cross_entropy_with_logits 函数计算交叉熵损失。此函数不需要模型的最后一层应用 Softmax 激活函数,也不需要对类标签进行独热编码。
def cross_entropy_loss(y_pred, y):
# Compute cross entropy loss with a sparse operation
sparse_ce = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=y_pred)
return tf.reduce_mean(sparse_ce)
编写一个基本的准确率函数,用于计算训练期间正确分类的比例。为了从 Softmax 输出生成类预测,返回与最大类概率相对应的索引。
def accuracy(y_pred, y):
# Compute accuracy after extracting class predictions
class_preds = tf.argmax(tf.nn.softmax(y_pred), axis=1)
is_equal = tf.equal(y, class_preds)
return tf.reduce_mean(tf.cast(is_equal, tf.float32))
训练模型
与标准梯度下降相比,使用优化器可以显着加快收敛速度。下面实现了 Adam 优化器。访问 优化器 指南,了解有关使用 TensorFlow Core 设计自定义优化器的更多信息。
class Adam:
def __init__(self, learning_rate=1e-3, beta_1=0.9, beta_2=0.999, ep=1e-7):
# Initialize optimizer parameters and variable slots
self.beta_1 = beta_1
self.beta_2 = beta_2
self.learning_rate = learning_rate
self.ep = ep
self.t = 1.
self.v_dvar, self.s_dvar = [], []
self.built = False
def apply_gradients(self, grads, vars):
# Initialize variables on the first call
if not self.built:
for var in vars:
v = tf.Variable(tf.zeros(shape=var.shape))
s = tf.Variable(tf.zeros(shape=var.shape))
self.v_dvar.append(v)
self.s_dvar.append(s)
self.built = True
# Update the model variables given their gradients
for i, (d_var, var) in enumerate(zip(grads, vars)):
self.v_dvar[i].assign(self.beta_1*self.v_dvar[i] + (1-self.beta_1)*d_var)
self.s_dvar[i].assign(self.beta_2*self.s_dvar[i] + (1-self.beta_2)*tf.square(d_var))
v_dvar_bc = self.v_dvar[i]/(1-(self.beta_1**self.t))
s_dvar_bc = self.s_dvar[i]/(1-(self.beta_2**self.t))
var.assign_sub(self.learning_rate*(v_dvar_bc/(tf.sqrt(s_dvar_bc) + self.ep)))
self.t += 1.
return
现在,编写一个自定义训练循环,使用小批量梯度下降更新 MLP 参数。使用小批量进行训练可以提高内存效率并加快收敛速度。
def train_step(x_batch, y_batch, loss, acc, model, optimizer):
# Update the model state given a batch of data
with tf.GradientTape() as tape:
y_pred = model(x_batch)
batch_loss = loss(y_pred, y_batch)
batch_acc = acc(y_pred, y_batch)
grads = tape.gradient(batch_loss, model.variables)
optimizer.apply_gradients(grads, model.variables)
return batch_loss, batch_acc
def val_step(x_batch, y_batch, loss, acc, model):
# Evaluate the model on given a batch of validation data
y_pred = model(x_batch)
batch_loss = loss(y_pred, y_batch)
batch_acc = acc(y_pred, y_batch)
return batch_loss, batch_acc
def train_model(mlp, train_data, val_data, loss, acc, optimizer, epochs):
# Initialize data structures
train_losses, train_accs = [], []
val_losses, val_accs = [], []
# Format training loop and begin training
for epoch in range(epochs):
batch_losses_train, batch_accs_train = [], []
batch_losses_val, batch_accs_val = [], []
# Iterate over the training data
for x_batch, y_batch in train_data:
# Compute gradients and update the model's parameters
batch_loss, batch_acc = train_step(x_batch, y_batch, loss, acc, mlp, optimizer)
# Keep track of batch-level training performance
batch_losses_train.append(batch_loss)
batch_accs_train.append(batch_acc)
# Iterate over the validation data
for x_batch, y_batch in val_data:
batch_loss, batch_acc = val_step(x_batch, y_batch, loss, acc, mlp)
batch_losses_val.append(batch_loss)
batch_accs_val.append(batch_acc)
# Keep track of epoch-level model performance
train_loss, train_acc = tf.reduce_mean(batch_losses_train), tf.reduce_mean(batch_accs_train)
val_loss, val_acc = tf.reduce_mean(batch_losses_val), tf.reduce_mean(batch_accs_val)
train_losses.append(train_loss)
train_accs.append(train_acc)
val_losses.append(val_loss)
val_accs.append(val_acc)
print(f"Epoch: {epoch}")
print(f"Training loss: {train_loss:.3f}, Training accuracy: {train_acc:.3f}")
print(f"Validation loss: {val_loss:.3f}, Validation accuracy: {val_acc:.3f}")
return train_losses, train_accs, val_losses, val_accs
使用 128 的批量大小训练 MLP 模型 10 个 epoch。GPU 或 TPU 等硬件加速器也可以帮助加快训练时间。
train_losses, train_accs, val_losses, val_accs = train_model(mlp_model, train_data, val_data,
loss=cross_entropy_loss, acc=accuracy,
optimizer=Adam(), epochs=10)
Epoch: 0 Training loss: 0.222, Training accuracy: 0.934 Validation loss: 0.120, Validation accuracy: 0.962 Epoch: 1 Training loss: 0.080, Training accuracy: 0.975 Validation loss: 0.099, Validation accuracy: 0.970 Epoch: 2 Training loss: 0.047, Training accuracy: 0.986 Validation loss: 0.092, Validation accuracy: 0.973 Epoch: 3 Training loss: 0.032, Training accuracy: 0.990 Validation loss: 0.091, Validation accuracy: 0.977 Epoch: 4 Training loss: 0.025, Training accuracy: 0.992 Validation loss: 0.100, Validation accuracy: 0.975 Epoch: 5 Training loss: 0.021, Training accuracy: 0.993 Validation loss: 0.101, Validation accuracy: 0.974 Epoch: 6 Training loss: 0.020, Training accuracy: 0.993 Validation loss: 0.106, Validation accuracy: 0.974 Epoch: 7 Training loss: 0.019, Training accuracy: 0.993 Validation loss: 0.096, Validation accuracy: 0.978 Epoch: 8 Training loss: 0.017, Training accuracy: 0.994 Validation loss: 0.108, Validation accuracy: 0.976 Epoch: 9 Training loss: 0.012, Training accuracy: 0.996 Validation loss: 0.103, Validation accuracy: 0.977
性能评估
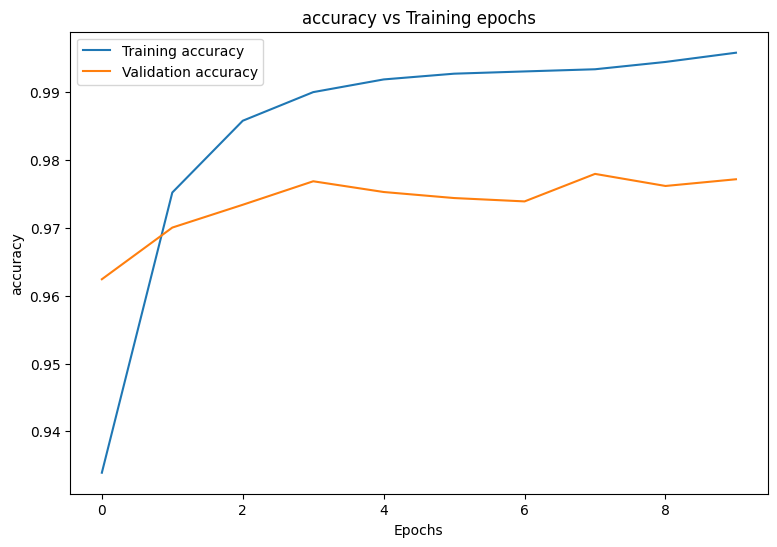
首先编写一个绘图函数,以可视化模型在训练期间的损失和准确率。
def plot_metrics(train_metric, val_metric, metric_type):
# Visualize metrics vs training Epochs
plt.figure()
plt.plot(range(len(train_metric)), train_metric, label = f"Training {metric_type}")
plt.plot(range(len(val_metric)), val_metric, label = f"Validation {metric_type}")
plt.xlabel("Epochs")
plt.ylabel(metric_type)
plt.legend()
plt.title(f"{metric_type} vs Training epochs");
plot_metrics(train_losses, val_losses, "cross entropy loss")
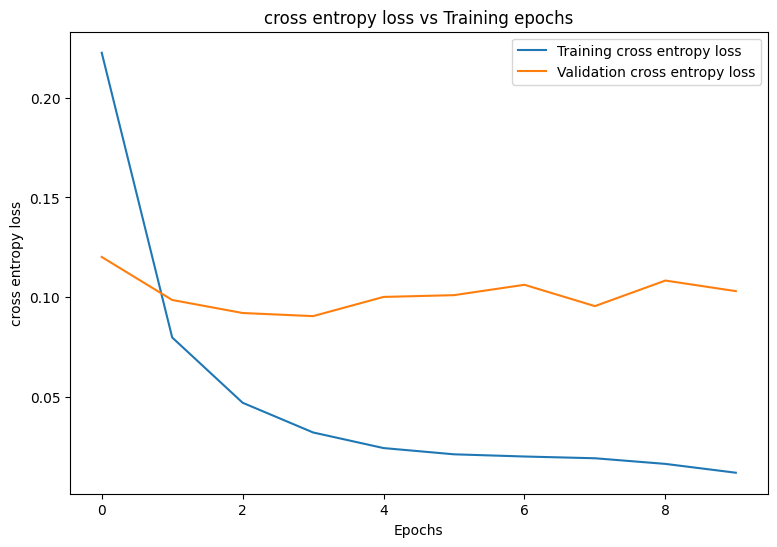
plot_metrics(train_accs, val_accs, "accuracy")
保存和加载模型
首先创建一个导出模块,该模块接收原始数据并执行以下操作
- 数据预处理
- 概率预测
- 类预测
class ExportModule(tf.Module):
def __init__(self, model, preprocess, class_pred):
# Initialize pre and postprocessing functions
self.model = model
self.preprocess = preprocess
self.class_pred = class_pred
@tf.function(input_signature=[tf.TensorSpec(shape=[None, None, None, None], dtype=tf.uint8)])
def __call__(self, x):
# Run the ExportModule for new data points
x = self.preprocess(x)
y = self.model(x)
y = self.class_pred(y)
return y
def preprocess_test(x):
# The export module takes in unprocessed and unlabeled data
x = tf.reshape(x, shape=[-1, 784])
x = x/255
return x
def class_pred_test(y):
# Generate class predictions from MLP output
return tf.argmax(tf.nn.softmax(y), axis=1)
现在可以使用 tf.saved_model.save 函数保存此导出模块。
mlp_model_export = ExportModule(model=mlp_model,
preprocess=preprocess_test,
class_pred=class_pred_test)
models = tempfile.mkdtemp()
save_path = os.path.join(models, 'mlp_model_export')
tf.saved_model.save(mlp_model_export, save_path)
INFO:tensorflow:Assets written to: /tmpfs/tmp/tmphtbcg1os/mlp_model_export/assets INFO:tensorflow:Assets written to: /tmpfs/tmp/tmphtbcg1os/mlp_model_export/assets
使用 tf.saved_model.load 加载保存的模型,并检查其在未见测试数据上的性能。
mlp_loaded = tf.saved_model.load(save_path)
def accuracy_score(y_pred, y):
# Generic accuracy function
is_equal = tf.equal(y_pred, y)
return tf.reduce_mean(tf.cast(is_equal, tf.float32))
x_test, y_test = tfds.load("mnist", split=['test'], batch_size=-1, as_supervised=True)[0]
test_classes = mlp_loaded(x_test)
test_acc = accuracy_score(test_classes, y_test)
print(f"Test Accuracy: {test_acc:.3f}")
Test Accuracy: 0.979
该模型在训练数据集中对手写数字进行了很好的分类,并且也很好地推广到了未见数据。现在,检查模型的类级准确率,以确保每个数字的性能良好。
print("Accuracy breakdown by digit:")
print("---------------------------")
label_accs = {}
for label in range(10):
label_ind = (y_test == label)
# extract predictions for specific true label
pred_label = test_classes[label_ind]
labels = y_test[label_ind]
# compute class-wise accuracy
label_accs[accuracy_score(pred_label, labels).numpy()] = label
for key in sorted(label_accs):
print(f"Digit {label_accs[key]}: {key:.3f}")
Accuracy breakdown by digit: --------------------------- Digit 4: 0.960 Digit 7: 0.967 Digit 3: 0.969 Digit 6: 0.973 Digit 8: 0.977 Digit 9: 0.984 Digit 0: 0.989 Digit 2: 0.990 Digit 5: 0.991 Digit 1: 0.993
看起来该模型在某些数字上的表现比其他数字差一些,这在许多多类分类问题中很常见。作为最后的练习,绘制模型预测及其对应真实标签的混淆矩阵,以收集更多类级见解。Sklearn 和 seaborn 具有用于生成和可视化混淆矩阵的函数。
import sklearn.metrics as sk_metrics
def show_confusion_matrix(test_labels, test_classes):
# Compute confusion matrix and normalize
plt.figure(figsize=(10,10))
confusion = sk_metrics.confusion_matrix(test_labels.numpy(),
test_classes.numpy())
confusion_normalized = confusion / confusion.sum(axis=1, keepdims=True)
axis_labels = range(10)
ax = sns.heatmap(
confusion_normalized, xticklabels=axis_labels, yticklabels=axis_labels,
cmap='Blues', annot=True, fmt='.4f', square=True)
plt.title("Confusion matrix")
plt.ylabel("True label")
plt.xlabel("Predicted label")
show_confusion_matrix(y_test, test_classes)
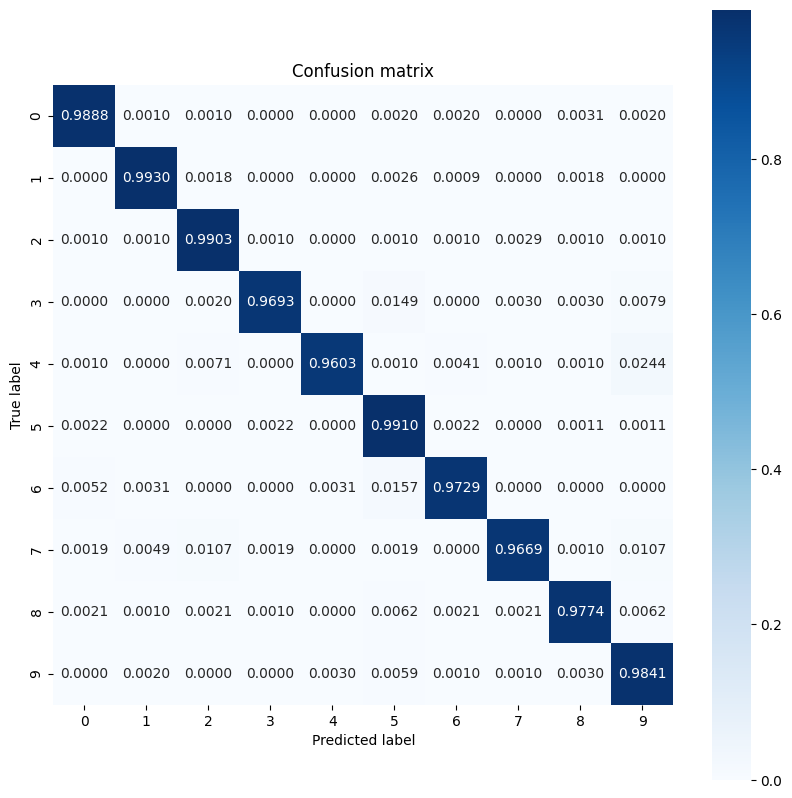
类级见解可以帮助识别错误分类的原因,并在未来的训练周期中提高模型性能。
结论
本笔记本介绍了一些使用 MLP 处理多类分类问题的技术。以下是一些可能有所帮助的额外提示
- 可以使用 TensorFlow Core API 构建具有高度可配置性的机器学习工作流程。
- 初始化方案可以帮助防止模型参数在训练期间消失或爆炸。
- 过拟合是神经网络的另一个常见问题,尽管在本教程中不是问题。访问 过拟合和欠拟合 教程,以获取更多帮助。
有关使用 TensorFlow Core API 的更多示例,请查看 指南。如果您想了解有关加载和准备数据的更多信息,请查看有关 图像数据加载 或 CSV 数据加载 的教程。
