版权所有 2023 TF-Agents 作者。
 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行
|
 在 GitHub 上查看源代码
|
 下载笔记本
|
简介
强化学习 (RL) 是一种通用框架，其中代理学习在环境中执行操作以最大化奖励。两个主要组件是环境，它代表要解决的问题，以及代理，它代表学习算法。
代理和环境不断相互作用。在每个时间步长，代理根据其策略 \(\pi(a_t|s_t)\) 对环境采取行动，其中 \(s_t\) 是来自环境的当前观察结果，并从环境接收奖励 \(r_{t+1}\) 和下一个观察结果 \(s_{t+1}\)。目标是改进策略以最大化奖励总和（回报）。
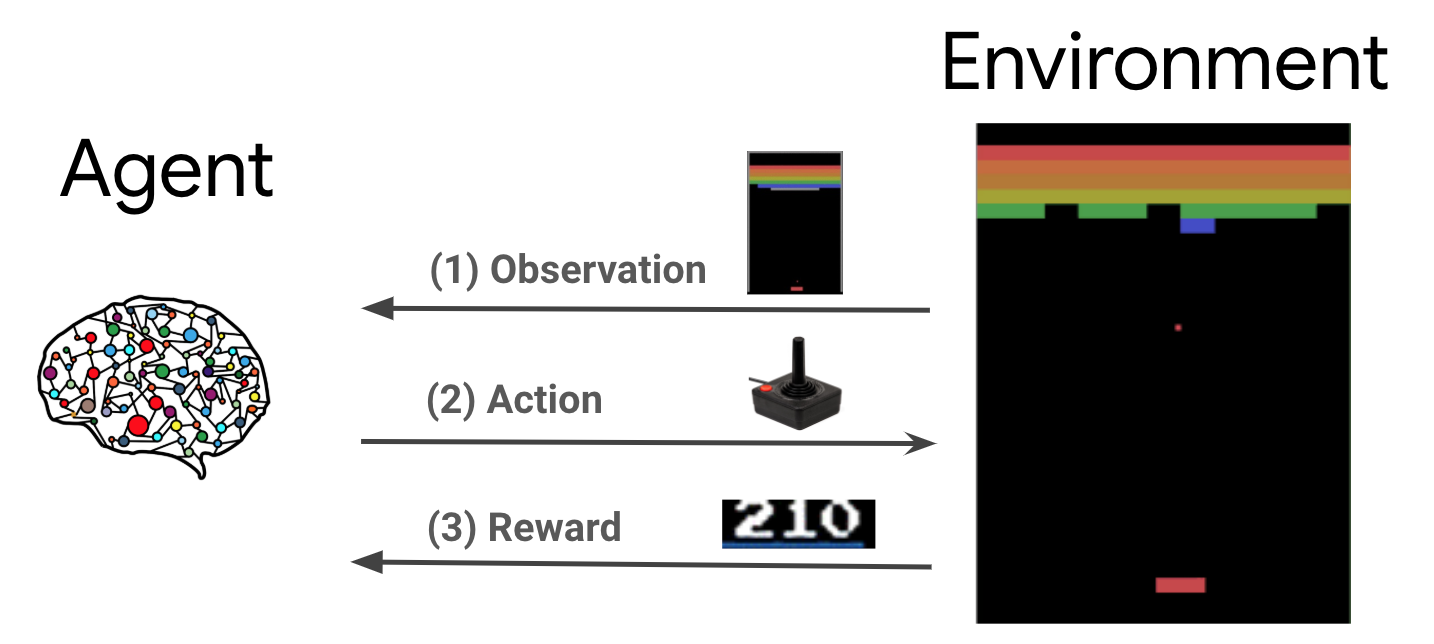
这是一个非常通用的框架，可以模拟各种顺序决策问题，例如游戏、机器人技术等。
Cartpole 环境
Cartpole 环境是最著名的经典强化学习问题之一（RL 的“Hello, World！”）。一根杆子连接到一辆小车上，小车可以在无摩擦的轨道上移动。杆子开始时直立，目标是通过控制小车来防止它倒下。
- 来自环境的观察结果 \(s_t\) 是一个 4 维向量，表示小车的位移和速度，以及杆子的角度和角速度。
- 代理可以通过采取两种行动之一 \(a_t\) 来控制系统：向右推小车 (+1) 或向左推小车 (-1)。
- 只要杆子保持直立，每个时间步长都会提供奖励 \(r_{t+1} = 1\)。当以下情况之一成立时，情节结束
- 杆子倾斜超过某个角度限制
- 小车移动到世界边缘之外
- 经过 200 个时间步长。
代理的目标是学习一个策略 \(\pi(a_t|s_t)\)，以最大化情节中奖励的总和 \(\sum_{t=0}^{T} \gamma^t r_t\)。这里 \(\gamma\) 是 \([0, 1]\) 中的折扣因子，它相对于即时奖励对未来奖励进行折扣。此参数有助于我们集中策略，使其更关注快速获得奖励。
DQN 代理
DeepMind 在 2015 年开发了DQN (深度 Q 网络) 算法。它能够通过将强化学习和深度神经网络大规模结合起来，解决各种 Atari 游戏（一些游戏达到超人类水平）。该算法是通过使用深度神经网络和一种称为经验回放的技术来增强经典 RL 算法 Q 学习而开发的。
Q 学习
Q 学习基于 Q 函数的概念。策略 \(\pi\) 的 Q 函数（也称为状态-动作值函数），\(Q^{\pi}(s, a)\)，衡量从状态 \(s\) 开始，首先采取行动 \(a\) 然后遵循策略 \(\pi\) 获得的预期回报或折扣奖励总和。我们将最优 Q 函数 \(Q^*(s, a)\) 定义为从观察结果 \(s\) 开始，采取行动 \(a\) 然后遵循最优策略获得的最大回报。最优 Q 函数服从以下贝尔曼最优方程
\(\begin{equation}Q^\ast(s, a) = \mathbb{E}[ r + \gamma \max_{a'} Q^\ast(s', a') ]\end{equation}\)
这意味着从状态 \(s\) 和行动 \(a\) 获得的最大回报是即时奖励 \(r\) 和随后遵循最优策略直到情节结束（即从下一个状态 \(s'\) 获得的最大奖励）获得的回报（按 \(\gamma\) 折扣）的总和。期望值是在即时奖励 \(r\) 的分布和可能的下一个状态 \(s'\) 上计算的。
Q 学习背后的基本思想是使用贝尔曼最优方程作为迭代更新 \(Q_{i+1}(s, a) \leftarrow \mathbb{E}\left[ r + \gamma \max_{a'} Q_{i}(s', a')\right]\)，并且可以证明这会收敛到最优 \(Q\) 函数，即 \(Q_i \rightarrow Q^*\) 作为 \(i \rightarrow \infty\)（参见DQN 论文）。
深度 Q 学习
对于大多数问题，将 \(Q\) 函数表示为包含每个 \(s\) 和 \(a\) 组合的值的表格是不切实际的。相反，我们训练一个函数逼近器，例如具有参数 \(\theta\) 的神经网络，来估计 Q 值，即 \(Q(s, a; \theta) \approx Q^*(s, a)\)。这可以通过在每个步骤 \(i\) 最小化以下损失来完成
\(\begin{equation}L_i(\theta_i) = \mathbb{E}_{s, a, r, s'\sim \rho(.)} \left[ (y_i - Q(s, a; \theta_i))^2 \right]\end{equation}\) 其中 \(y_i = r + \gamma \max_{a'} Q(s', a'; \theta_{i-1})\)
这里，\(y_i\) 被称为 TD（时间差）目标，\(y_i - Q\) 被称为 TD 误差。\(\rho\) 代表行为分布，即从环境收集的转换 \(\{s, a, r, s'\}\) 的分布。
请注意，来自前一次迭代的参数 \(\theta_{i-1}\) 是固定的，不会更新。在实践中，我们使用来自几个迭代之前的网络参数的快照，而不是最后一次迭代。此副本称为目标网络。
Q-学习是一种非策略算法，它学习关于贪婪策略\(a = \max_{a} Q(s, a; \theta)\)的信息，同时使用不同的行为策略在环境中行动/收集数据。这种行为策略通常是\(\epsilon\)-贪婪策略，它以\(1-\epsilon\)的概率选择贪婪动作，以\(\epsilon\)的概率选择随机动作，以确保对状态-动作空间的良好覆盖。
经验回放
为了避免计算 DQN 损失中的完整期望，我们可以使用随机梯度下降来最小化它。如果损失是使用最后一个转移\(\{s, a, r, s'\}\)计算的，这将简化为标准 Q-学习。
Atari DQN 工作引入了一种称为经验回放的技术，使网络更新更加稳定。在数据收集的每个时间步长，转移都会被添加到一个称为回放缓冲区的循环缓冲区中。然后在训练期间，我们不是只使用最新的转移来计算损失及其梯度，而是使用从回放缓冲区中采样的一个小型批次的转移来计算它们。这有两个优点：通过在许多更新中重复使用每个转移来提高数据效率，以及通过使用批次中不相关的转移来提高稳定性。
TF-Agents 中的 Cartpole 上的 DQN
TF-Agents 提供了训练 DQN 代理所需的所有组件，例如代理本身、环境、策略、网络、回放缓冲区、数据收集循环和指标。这些组件被实现为 Python 函数或 TensorFlow 图操作，我们还拥有用于它们之间转换的包装器。此外，TF-Agents 支持 TensorFlow 2.0 模式，这使我们能够以命令式模式使用 TF。