TensorFlow Lattice 是一个实现灵活、可控且可解释的基于格子的模型的库。该库使您能够通过常识或策略驱动的 形状约束 将领域知识注入学习过程。这是通过一组 Keras 层 完成的,这些层可以满足单调性、凸性和成对信任等约束。该库还提供易于设置的 预制模型。
概念
本节是对 单调校准插值查找表 (JMLR 2016) 中描述的简化版本。
格
格 是一个插值查找表,可以近似数据中任意输入-输出关系。它将一个规则网格叠加到您的输入空间上,并学习网格顶点处输出的值。对于测试点 \(x\),\(f(x)\) 从围绕 \(x\) 的格值线性插值。
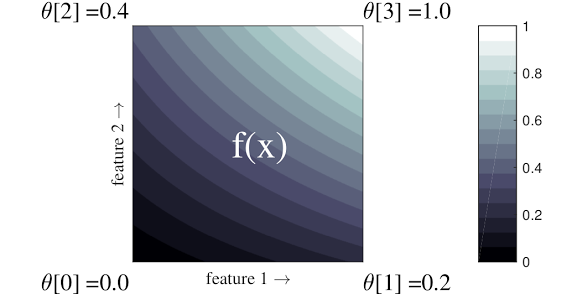
上面的简单示例是一个具有 2 个输入特征和 4 个参数的函数:\(\theta=[0, 0.2, 0.4, 1]\),它们是函数在输入空间角点的值;函数的其余部分是从这些参数插值的。
函数 \(f(x)\) 可以捕获特征之间的非线性交互。您可以将格参数视为在规则网格上在地面上设置的杆的高度,而生成的函数就像紧贴四个杆的布一样。
对于 \(D\) 个特征和每个维度上的 2 个顶点,规则格将具有 \(2^D\) 个参数。为了拟合更灵活的函数,您可以在特征空间上指定一个更细粒度的格,在每个维度上具有更多顶点。格回归函数是连续的,并且分段无限可微。
校准
假设前面的示例格表示使用特征计算的建议的当地咖啡店的用户满意度
- 咖啡价格,范围为 0 到 20 美元
- 到用户的距离,范围为 0 到 30 公里
我们希望我们的模型学习用户对当地咖啡店建议的满意度。TensorFlow Lattice 模型可以使用分段线性函数(使用 tfl.layers.PWLCalibration)来校准和规范化输入特征,使其处于格接受的范围内:在上面的示例格中为 0.0 到 1.0。以下显示了具有 10 个关键点的校准函数示例
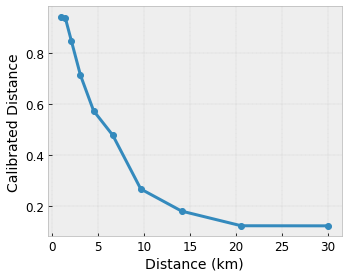
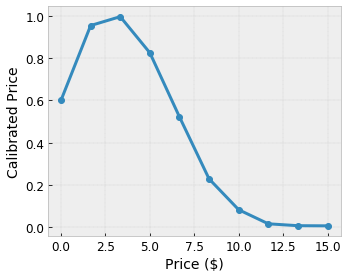
通常,将特征的分位数用作输入关键点是一个好主意。TensorFlow Lattice 预制模型 可以自动将输入关键点设置为特征分位数。
对于分类特征,TensorFlow Lattice 提供分类校准(使用 tfl.layers.CategoricalCalibration),具有类似的输出边界,以馈送到格中。
集成
格层的参数数量随着输入特征数量的增加呈指数增长,因此不能很好地扩展到非常高的维度。为了克服这一限制,TensorFlow Lattice 提供了格的集成,这些集成组合(平均)了几个微型格,这使得模型能够在特征数量上线性增长。
该库提供了这些集成的两种变体
随机微型格 (RTL):每个子模型使用特征的随机子集(有放回地)。
晶体:晶体算法首先训练一个预拟合模型,该模型估计成对特征交互。然后,它安排最终集成,使得具有更多非线性交互的特征位于同一个格中。
为什么选择 TensorFlow Lattice?
您可以在此 TF 博客文章 中找到 TensorFlow Lattice 的简要介绍。
可解释性
由于每一层的参数都是该层的输出,因此很容易分析、理解和调试模型的每个部分。
准确且灵活的模型
使用细粒度的格,您可以使用单个格层获得任意复杂的函数。在实践中,使用多层校准器和格通常效果很好,并且可以匹配或优于大小相似的 DNN 模型。
常识形状约束
现实世界中的训练数据可能不足以代表运行时数据。DNN 或森林等灵活的 ML 解决方案通常在输入空间中未被训练数据覆盖的部分表现出意外甚至狂野的行为。当违反策略或公平性约束时,这种行为尤其成问题。
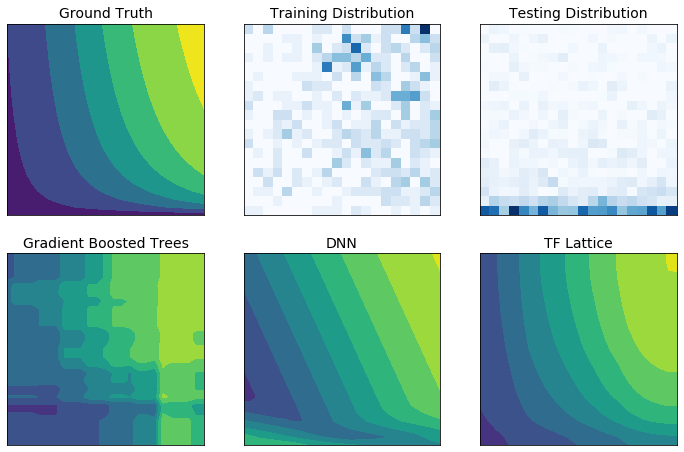
即使常见的正则化形式可以导致更合理的推断,标准正则化器也不能保证在整个输入空间中合理的模型行为,尤其是在高维输入的情况下。切换到更简单的模型,这些模型具有更可控和可预测的行为,可能会对模型精度造成严重损失。
TF Lattice 使得继续使用灵活的模型成为可能,但提供了多种选择,可以通过语义上有意义的常识或策略驱动的 形状约束 将领域知识注入学习过程
- 单调性:您可以指定输出应该仅相对于输入增加/减少。在我们的示例中,您可能希望指定到咖啡店的距离增加应该只会降低预测的用户偏好。
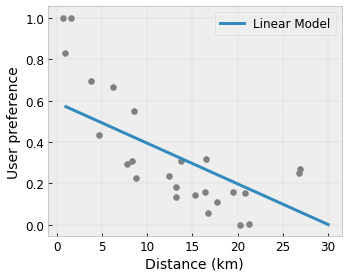
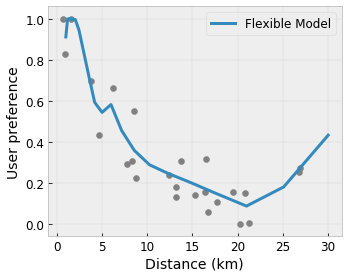
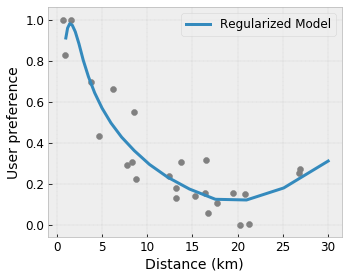
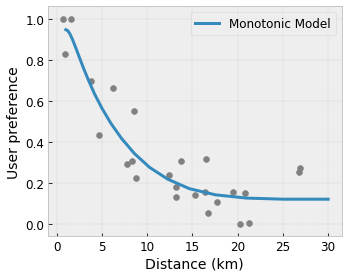
凸性/凹性: 您可以指定函数形状可以是凸的或凹的。与单调性混合,这可以强制函数相对于给定特征表示递减收益。
单峰性: 您可以指定函数应该有一个唯一的峰值或唯一的谷值。这使您可以表示相对于特征具有“最佳点”的函数。
成对信任: 此约束作用于一对特征,并建议一个输入特征在语义上反映对另一个特征的信任。例如,更多的评论数量会让你对餐厅的平均星级评分更有信心。当评论数量较高时,模型将对星级评分更敏感(即,相对于评分将具有更大的斜率)。
使用正则化器控制灵活性
除了形状约束之外,TensorFlow Lattice 还提供了一些正则化器来控制每一层函数的灵活性和平滑度。
拉普拉斯正则化器: 格子/校准顶点/关键点的输出将被正则化到它们各自邻居的值。这会导致一个“更平坦”的函数。
Hessian 正则化器: 这会惩罚 PWL 校准层的导数,使函数“更线性”。
皱纹正则化器: 这会惩罚 PWL 校准层的二阶导数,以避免曲率的突然变化。它使函数更平滑。
扭转正则化器: 格子的输出将被正则化以防止特征之间的扭转。换句话说,模型将被正则化以使特征贡献之间的独立性。
与其他 Keras 层混合搭配
您可以将 TF Lattice 层与其他 Keras 层结合使用,以构建部分约束或正则化模型。例如,格子或 PWL 校准层可以在包括嵌入或其他 Keras 层的更深层网络的最后一层使用。
论文
- 通过单调性形状约束实现义务伦理,Serena Wang,Maya Gupta,人工智能与统计国际会议 (AISTATS),2020 年
- 集合函数的形状约束,Andrew Cotter,Maya Gupta,H. Jiang,Erez Louidor,Jim Muller,Taman Narayan,Serena Wang,Tao Zhu。机器学习国际会议 (ICML),2019 年
- 递减收益形状约束用于可解释性和正则化,Maya Gupta,Dara Bahri,Andrew Cotter,Kevin Canini,神经信息处理系统进展 (NeurIPS),2018 年
- 深度格子网络和部分单调函数,Seungil You,Kevin Canini,David Ding,Jan Pfeifer,Maya R. Gupta,神经信息处理系统进展 (NeurIPS),2017 年
- 使用格子集合实现快速灵活的单调函数,Mahdi Milani Fard,Kevin Canini,Andrew Cotter,Jan Pfeifer,Maya Gupta,神经信息处理系统进展 (NeurIPS),2016 年
- 单调校准插值查找表,Maya Gupta,Andrew Cotter,Jan Pfeifer,Konstantin Voevodski,Kevin Canini,Alexander Mangylov,Wojciech Moczydlowski,Alexander van Esbroeck,机器学习研究杂志 (JMLR),2016 年
- 用于高效函数评估的优化回归,Eric Garcia,Raman Arora,Maya R. Gupta,IEEE 图像处理汇刊,2012 年
- 格子回归,Eric Garcia,Maya Gupta,神经信息处理系统进展 (NeurIPS),2009 年
教程和 API 文档
对于常见的模型架构,您可以使用 Keras 预制模型。您还可以使用 TF Lattice Keras 层 创建自定义模型,或与其他 Keras 层混合搭配。查看 完整的 API 文档 以了解更多详细信息。
