 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
本教程将演示使用 TensorFlow Federated 训练具有用户级差分隐私的模型的推荐最佳实践。我们将使用 Abadi 等人,“具有差分隐私的深度学习” 中的 DP-SGD 算法,该算法针对 McMahan 等人,“学习差分隐私循环语言模型” 中的联邦环境中的用户级 DP 进行修改。
差分隐私 (DP) 是一种广泛使用的用于在执行学习任务时限制和量化敏感数据的隐私泄露的方法。使用用户级 DP 训练模型可以保证模型不太可能从任何个人的数据中学习到任何重要信息,但仍然可以(希望!)学习存在于许多客户端数据中的模式。
我们将使用联邦 EMNIST 数据集训练模型。效用和隐私之间存在固有的权衡,训练具有高隐私且性能与最先进的非私有模型一样好的模型可能很困难。为了在本教程中快速完成,我们将只训练 100 轮,为了演示如何以高隐私进行训练,牺牲了一些质量。如果我们使用更多训练轮次,我们当然可以获得一个精度略高的私有模型,但不会像没有 DP 的模型那样高。
在我们开始之前
首先,让我们确保笔记本连接到具有相关组件编译的后台。
pip install --quiet --upgrade dp-accountingpip install --quiet --upgrade tensorflow-federated
本教程需要的一些导入。我们将使用 tensorflow_federated(用于在分散数据上进行机器学习和其他计算的开源框架)以及 dp_accounting(用于分析差分隐私算法的开源库)。
import collections
import dp_accounting
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_federated as tff
运行以下“Hello World”示例以确保 TFF 环境已正确设置。如果它不起作用,请参阅 安装 指南以获取说明。
@tff.federated_computation
def hello_world():
return 'Hello, World!'
hello_world()
b'Hello, World!'
下载并预处理联邦 EMNIST 数据集。
def get_emnist_dataset():
emnist_train, emnist_test = tff.simulation.datasets.emnist.load_data(
only_digits=True)
def element_fn(element):
return collections.OrderedDict(
x=tf.expand_dims(element['pixels'], -1), y=element['label'])
def preprocess_train_dataset(dataset):
# Use buffer_size same as the maximum client dataset size,
# 418 for Federated EMNIST
return (dataset.map(element_fn)
.shuffle(buffer_size=418)
.repeat(1)
.batch(32, drop_remainder=False))
def preprocess_test_dataset(dataset):
return dataset.map(element_fn).batch(128, drop_remainder=False)
emnist_train = emnist_train.preprocess(preprocess_train_dataset)
emnist_test = preprocess_test_dataset(
emnist_test.create_tf_dataset_from_all_clients())
return emnist_train, emnist_test
train_data, test_data = get_emnist_dataset()
定义我们的模型。
def my_model_fn():
model = tf.keras.models.Sequential([
tf.keras.layers.Reshape(input_shape=(28, 28, 1), target_shape=(28 * 28,)),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(200, activation=tf.nn.relu),
tf.keras.layers.Dense(10)])
return tff.learning.models.from_keras_model(
keras_model=model,
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
input_spec=test_data.element_spec,
metrics=[tf.keras.metrics.SparseCategoricalAccuracy()])
确定模型的噪声敏感度。
为了获得用户级 DP 保证,我们必须以两种方式更改基本的联邦平均算法。首先,必须在客户端模型更新传输到服务器之前对其进行裁剪,以限制任何一个客户端的最大影响。其次,服务器必须在平均之前向用户更新的总和添加足够的噪声,以掩盖最坏情况下的客户端影响。
对于裁剪,我们使用 Andrew 等人 2021 年的“具有自适应裁剪的差分隐私学习” 中的自适应裁剪方法,因此无需显式设置裁剪范数。
添加噪声通常会降低模型的效用,但我们可以使用两个旋钮来控制每轮平均更新中的噪声量:添加到总和的 Gaussian 噪声的标准差,以及平均中的客户端数量。我们的策略是首先确定模型在每轮具有相对较少的客户端的情况下可以容忍多少噪声,同时对模型效用造成的损失可以接受。然后,为了训练最终模型,我们可以增加总和中的噪声量,同时按比例增加每轮的客户端数量(假设数据集足够大以支持每轮这么多客户端)。这不太可能显着影响模型质量,因为唯一的影响是减少由于客户端采样造成的方差(事实上,我们将验证它在我们的案例中没有影响)。
为此,我们首先训练了一系列模型,每轮 50 个客户端,并增加了噪声量。具体来说,我们增加了“noise_multiplier”,它是噪声标准差与裁剪范数的比率。由于我们使用的是自适应裁剪,这意味着噪声的实际幅度会随着轮次的改变而改变。
total_clients = len(train_data.client_ids)
def train(rounds, noise_multiplier, clients_per_round, data_frame):
# Using the `dp_aggregator` here turns on differential privacy with adaptive
# clipping.
aggregation_factory = tff.learning.model_update_aggregator.dp_aggregator(
noise_multiplier, clients_per_round)
# We use Poisson subsampling which gives slightly tighter privacy guarantees
# compared to having a fixed number of clients per round. The actual number of
# clients per round is stochastic with mean clients_per_round.
sampling_prob = clients_per_round / total_clients
# Build a federated averaging process.
# Typically a non-adaptive server optimizer is used because the noise in the
# updates can cause the second moment accumulators to become very large
# prematurely.
learning_process = tff.learning.algorithms.build_unweighted_fed_avg(
my_model_fn,
client_optimizer_fn=lambda: tf.keras.optimizers.SGD(0.01),
server_optimizer_fn=lambda: tf.keras.optimizers.SGD(1.0, momentum=0.9),
model_aggregator=aggregation_factory)
eval_process = tff.learning.build_federated_evaluation(my_model_fn)
# Training loop.
state = learning_process.initialize()
for round in range(rounds):
if round % 5 == 0:
model_weights = learning_process.get_model_weights(state)
metrics = eval_process(model_weights, [test_data])['eval']
if round < 25 or round % 25 == 0:
print(f'Round {round:3d}: {metrics}')
data_frame = data_frame.append({'Round': round,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
# Sample clients for a round. Note that if your dataset is large and
# sampling_prob is small, it would be faster to use gap sampling.
x = np.random.uniform(size=total_clients)
sampled_clients = [
train_data.client_ids[i] for i in range(total_clients)
if x[i] < sampling_prob]
sampled_train_data = [
train_data.create_tf_dataset_for_client(client)
for client in sampled_clients]
# Use selected clients for update.
result = learning_process.next(state, sampled_train_data)
state = result.state
metrics = result.metrics
model_weights = learning_process.get_model_weights(state)
metrics = eval_process(model_weights, [test_data])['eval']
print(f'Round {rounds:3d}: {metrics}')
data_frame = data_frame.append({'Round': rounds,
'NoiseMultiplier': noise_multiplier,
**metrics}, ignore_index=True)
return data_frame
data_frame = pd.DataFrame()
rounds = 100
clients_per_round = 50
for noise_multiplier in [0.0, 0.5, 0.75, 1.0]:
print(f'Starting training with noise multiplier: {noise_multiplier}')
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
print()
Starting training with noise multiplier: 0.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.112289384), ('loss', 2.5190482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.19075724), ('loss', 2.2449977)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.18115693), ('loss', 2.163907)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49970612), ('loss', 2.01017)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5333317), ('loss', 1.8350543)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.5828517), ('loss', 1.6551636)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7352077), ('loss', 0.8700141)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7769152), ('loss', 0.6992781)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.8049814), ('loss', 0.62453026)])
Starting training with noise multiplier: 0.5
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.09526841), ('loss', 2.4332638)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.20128821), ('loss', 2.2664592)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.35472178), ('loss', 2.130336)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.5480995), ('loss', 1.9713942)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.42246276), ('loss', 1.8045483)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.624902), ('loss', 1.4785467)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.7265625), ('loss', 0.85801566)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.77720904), ('loss', 0.70615387)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7702537), ('loss', 0.72331005)])
Starting training with noise multiplier: 0.75
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.098672606), ('loss', 2.422002)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.11794671), ('loss', 2.2227976)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.3208513), ('loss', 2.083766)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.49752644), ('loss', 1.8728142)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5816761), ('loss', 1.6084186)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.62896746), ('loss', 1.378527)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.73153406), ('loss', 0.8705139)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.7789724), ('loss', 0.7113147)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.70944357), ('loss', 0.89495045)])
Starting training with noise multiplier: 1.0
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.12002841), ('loss', 2.60482)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.104574844), ('loss', 2.3388205)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.29966694), ('loss', 2.089262)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.4067398), ('loss', 1.9109797)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5123677), ('loss', 1.6472703)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.56416535), ('loss', 1.4362282)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.62323666), ('loss', 1.1682972)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.55968356), ('loss', 1.4779186)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.382837), ('loss', 1.9680436)])
现在我们可以可视化这些运行的评估集准确率和损失。
import matplotlib.pyplot as plt
import seaborn as sns
def make_plot(data_frame):
plt.figure(figsize=(15, 5))
dff = data_frame.rename(
columns={'sparse_categorical_accuracy': 'Accuracy', 'loss': 'Loss'})
plt.subplot(121)
sns.lineplot(data=dff, x='Round', y='Accuracy', hue='NoiseMultiplier', palette='dark')
plt.subplot(122)
sns.lineplot(data=dff, x='Round', y='Loss', hue='NoiseMultiplier', palette='dark')
make_plot(data_frame)
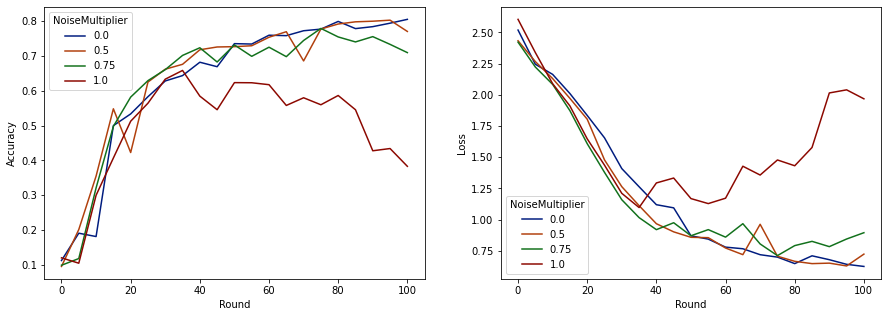
看起来,每轮 50 个预期客户端,该模型可以容忍高达 0.5 的噪声乘数,而不会降低模型质量。0.75 的噪声乘数似乎会导致模型质量略有下降,而 1.0 则会导致模型发散。
通常,模型质量和隐私之间存在权衡。我们使用的噪声越大,在相同的训练时间和客户端数量下,我们可以获得的隐私就越高。相反,如果噪声较小,我们可能会有一个更准确的模型,但我们需要在每轮训练中使用更多客户端才能达到我们的目标隐私级别。
通过上面的实验,我们可能会认为 0.75 时的模型质量略有下降是可以接受的,以便更快地训练最终模型,但假设我们想要匹配 0.5 噪声乘数模型的性能。
现在我们可以使用 dp_accounting 函数来确定我们需要多少个预期客户端才能获得可接受的隐私。标准做法是选择比数据集中的记录数量小得多的 delta。该数据集共有 3383 个训练用户,因此我们的目标是 (2, 1e-5)-DP。
我们使用 dp_accounting.calibrate_dp_mechanism 在每轮客户端数量上进行搜索。我们用来估计给定 dp_accounting.DpEvent 的隐私的隐私会计师 (RdpAccountant) 基于 Wang 等人 (2018) 和 Mironov 等人 (2019)。
total_clients = 3383
noise_to_clients_ratio = 0.01
target_delta = 1e-5
target_eps = 2
# Initialize arguments to dp_accounting.calibrate_dp_mechanism.
# No-arg callable that returns a fresh accountant.
make_fresh_accountant = dp_accounting.rdp.RdpAccountant
# Create function that takes expected clients per round and returns a
# dp_accounting.DpEvent representing the full training process.
def make_event_from_param(clients_per_round):
q = clients_per_round / total_clients
noise_multiplier = clients_per_round * noise_to_clients_ratio
gaussian_event = dp_accounting.GaussianDpEvent(noise_multiplier)
sampled_event = dp_accounting.PoissonSampledDpEvent(q, gaussian_event)
composed_event = dp_accounting.SelfComposedDpEvent(sampled_event, rounds)
return composed_event
# Create object representing the search range [1, 3383].
bracket_interval = dp_accounting.ExplicitBracketInterval(1, total_clients)
# Perform search for smallest clients_per_round achieving the target privacy.
clients_per_round = dp_accounting.calibrate_dp_mechanism(
make_fresh_accountant, make_event_from_param, target_eps, target_delta,
bracket_interval, discrete=True
)
noise_multiplier = clients_per_round * noise_to_clients_ratio
print(f'To get ({target_eps}, {target_delta})-DP, use {clients_per_round} '
f'clients with noise multiplier {noise_multiplier}.')
To get (2, 1e-05)-DP, use 120 clients with noise multiplier 1.2.
现在我们可以训练我们的最终私有模型以供发布。
rounds = 100
noise_multiplier = 1.2
clients_per_round = 120
data_frame = pd.DataFrame()
data_frame = train(rounds, noise_multiplier, clients_per_round, data_frame)
make_plot(data_frame)
Round 0: OrderedDict([('sparse_categorical_accuracy', 0.08260678), ('loss', 2.6334999)])
Round 5: OrderedDict([('sparse_categorical_accuracy', 0.1492212), ('loss', 2.259542)])
Round 10: OrderedDict([('sparse_categorical_accuracy', 0.28847474), ('loss', 2.155699)])
Round 15: OrderedDict([('sparse_categorical_accuracy', 0.3989518), ('loss', 2.0156953)])
Round 20: OrderedDict([('sparse_categorical_accuracy', 0.5086697), ('loss', 1.8261365)])
Round 25: OrderedDict([('sparse_categorical_accuracy', 0.6204692), ('loss', 1.5602393)])
Round 50: OrderedDict([('sparse_categorical_accuracy', 0.70008814), ('loss', 0.91155165)])
Round 75: OrderedDict([('sparse_categorical_accuracy', 0.78421336), ('loss', 0.6820159)])
Round 100: OrderedDict([('sparse_categorical_accuracy', 0.7955525), ('loss', 0.6585961)])
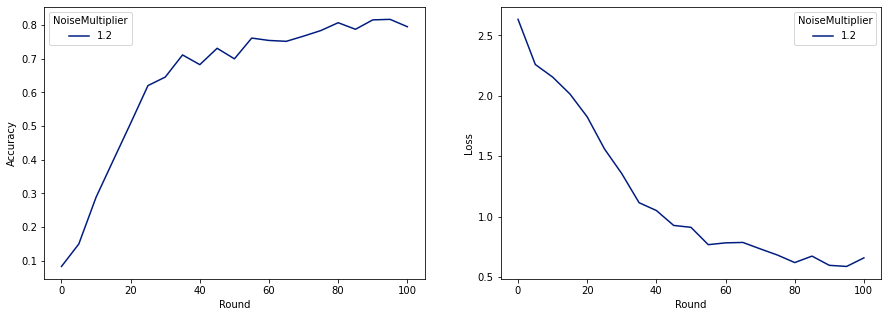
正如我们所见,最终模型的损失和准确率与未加噪声训练的模型相似,但这个模型满足 (2, 1e-5)-DP。
