 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
量子计算机已证明在某些问题领域可以提供计算优势。量子强化学习 (QRL) 领域旨在通过设计依赖于量子计算模型的 RL 代理来利用这一优势。
在本教程中,您将实现两种基于参数化/变分量子电路 (PQC 或 VQC) 的强化学习算法,即策略梯度和深度 Q 学习实现。这些算法由 [1] Jerbi 等人 和 [2] Skolik 等人 分别提出。
您将在 TFQ 中实现带有数据重新上传的 PQC,并将其用作
- 使用策略梯度方法训练的 RL 策略,
- 使用深度 Q 学习训练的 Q 函数逼近器,
每个都解决 CartPole-v1,这是 OpenAI Gym 的基准任务。请注意,如 [1] 和 [2] 中所示,这些代理还可以用于解决 OpenAI Gym 中的其他任务环境,例如 FrozenLake-v0、MountainCar-v0 或 Acrobot-v1。
此实现的功能
- 您将学习如何使用
tfq.layers.ControlledPQC实现带有数据重新上传的 PQC,它出现在 QML 的许多应用中。此实现还自然地允许在 PQC 的输入端使用可训练的缩放参数,以提高其表达能力, - 您将学习如何使用可训练权重实现 PQC 输出端的可观测值,以允许灵活的输出值范围,
- 您将学习如何使用
tf.keras.Model使用非平凡的 ML 损失函数(即与model.compile和model.fit不兼容)进行训练,使用tf.GradientTape。
设置
安装 TensorFlow
pip install tensorflow==2.15.0
安装 TensorFlow Quantum
pip install tensorflow-quantum==0.7.3
安装 Gym
pip install gym==0.18.0
现在导入 TensorFlow 和模块依赖项
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
import tensorflow as tf
import tensorflow_quantum as tfq
import gym, cirq, sympy
import numpy as np
from functools import reduce
from collections import deque, defaultdict
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
tf.get_logger().setLevel('ERROR')
1. 使用数据重新上传构建 PQC
在您要实现的两种 RL 算法的核心是一个 PQC,它将环境中的代理状态 \(s\)(即,一个 numpy 数组)作为输入,并输出一个期望值向量。然后对这些期望值进行后处理,以生成代理策略 \(\pi(a|s)\) 或近似 Q 值 \(Q(s,a)\)。通过这种方式,PQC 在现代深度 RL 算法中扮演着与深度神经网络类似的角色。
在 PQC 中对输入向量进行编码的一种流行方法是使用单量子位旋转,其中旋转角度由该输入向量的分量控制。为了得到一个高表达能力的模型,这些单量子位编码不会在 PQC 中只执行一次,而是在多个“重新上传”中执行,并与变分门交错。这种 PQC 的布局如下所示
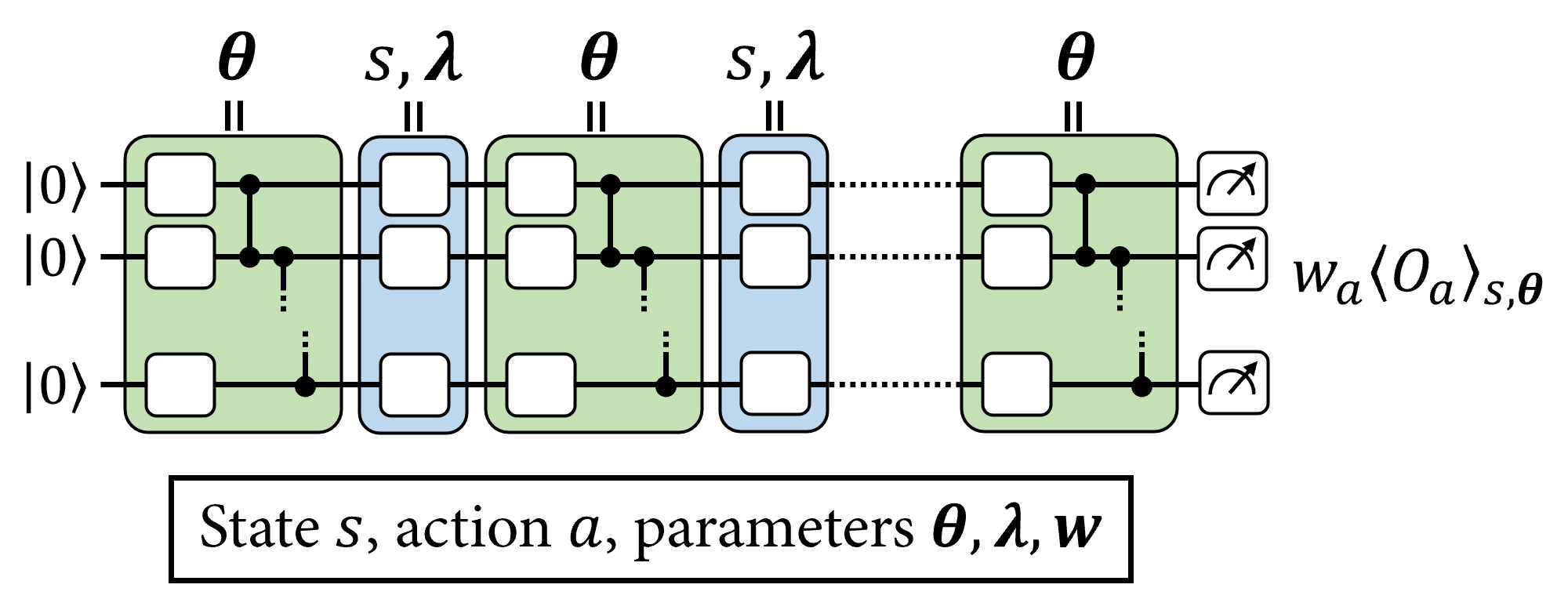
正如在 [1] 和 [2] 中所讨论的,进一步提高数据重新上传 PQC 的表达能力和可训练性的方法是为 PQC 的每个编码门使用可训练输入缩放参数 \(\boldsymbol{\lambda}\),并在其输出处使用可训练观测权重 \(\boldsymbol{w}\)。
1.1 用于 ControlledPQC 的 Cirq 电路
第一步是在 Cirq 中实现用作 PQC 的量子电路。为此,首先定义要在电路中应用的基本酉算子,即任意单量子位旋转和 CZ 门的纠缠层
def one_qubit_rotation(qubit, symbols):
"""
Returns Cirq gates that apply a rotation of the bloch sphere about the X,
Y and Z axis, specified by the values in `symbols`.
"""
return [cirq.rx(symbols[0])(qubit),
cirq.ry(symbols[1])(qubit),
cirq.rz(symbols[2])(qubit)]
def entangling_layer(qubits):
"""
Returns a layer of CZ entangling gates on `qubits` (arranged in a circular topology).
"""
cz_ops = [cirq.CZ(q0, q1) for q0, q1 in zip(qubits, qubits[1:])]
cz_ops += ([cirq.CZ(qubits[0], qubits[-1])] if len(qubits) != 2 else [])
return cz_ops
现在,使用这些函数生成 Cirq 电路
def generate_circuit(qubits, n_layers):
"""Prepares a data re-uploading circuit on `qubits` with `n_layers` layers."""
# Number of qubits
n_qubits = len(qubits)
# Sympy symbols for variational angles
params = sympy.symbols(f'theta(0:{3*(n_layers+1)*n_qubits})')
params = np.asarray(params).reshape((n_layers + 1, n_qubits, 3))
# Sympy symbols for encoding angles
inputs = sympy.symbols(f'x(0:{n_layers})'+f'_(0:{n_qubits})')
inputs = np.asarray(inputs).reshape((n_layers, n_qubits))
# Define circuit
circuit = cirq.Circuit()
for l in range(n_layers):
# Variational layer
circuit += cirq.Circuit(one_qubit_rotation(q, params[l, i]) for i, q in enumerate(qubits))
circuit += entangling_layer(qubits)
# Encoding layer
circuit += cirq.Circuit(cirq.rx(inputs[l, i])(q) for i, q in enumerate(qubits))
# Last varitional layer
circuit += cirq.Circuit(one_qubit_rotation(q, params[n_layers, i]) for i,q in enumerate(qubits))
return circuit, list(params.flat), list(inputs.flat)
检查这是否会产生在变分层和编码层之间交替的电路。
n_qubits, n_layers = 3, 1
qubits = cirq.GridQubit.rect(1, n_qubits)
circuit, _, _ = generate_circuit(qubits, n_layers)
SVGCircuit(circuit)
findfont: Font family ['Arial'] not found. Falling back to DejaVu Sans.
1.2 使用 ControlledPQC 的 ReUploadingPQC 层
要从上图构建重新上传 PQC,您可以创建一个自定义 Keras 层。此层将管理可训练参数(变分角 \(\boldsymbol{\theta}\) 和输入缩放参数 \(\boldsymbol{\lambda}\))并将输入值(输入状态 \(s\))解析为电路中的适当符号。
class ReUploadingPQC(tf.keras.layers.Layer):
"""
Performs the transformation (s_1, ..., s_d) -> (theta_1, ..., theta_N, lmbd[1][1]s_1, ..., lmbd[1][M]s_1,
......., lmbd[d][1]s_d, ..., lmbd[d][M]s_d) for d=input_dim, N=theta_dim and M=n_layers.
An activation function from tf.keras.activations, specified by `activation` ('linear' by default) is
then applied to all lmbd[i][j]s_i.
All angles are finally permuted to follow the alphabetical order of their symbol names, as processed
by the ControlledPQC.
"""
def __init__(self, qubits, n_layers, observables, activation="linear", name="re-uploading_PQC"):
super(ReUploadingPQC, self).__init__(name=name)
self.n_layers = n_layers
self.n_qubits = len(qubits)
circuit, theta_symbols, input_symbols = generate_circuit(qubits, n_layers)
theta_init = tf.random_uniform_initializer(minval=0.0, maxval=np.pi)
self.theta = tf.Variable(
initial_value=theta_init(shape=(1, len(theta_symbols)), dtype="float32"),
trainable=True, name="thetas"
)
lmbd_init = tf.ones(shape=(self.n_qubits * self.n_layers,))
self.lmbd = tf.Variable(
initial_value=lmbd_init, dtype="float32", trainable=True, name="lambdas"
)
# Define explicit symbol order.
symbols = [str(symb) for symb in theta_symbols + input_symbols]
self.indices = tf.constant([symbols.index(a) for a in sorted(symbols)])
self.activation = activation
self.empty_circuit = tfq.convert_to_tensor([cirq.Circuit()])
self.computation_layer = tfq.layers.ControlledPQC(circuit, observables)
def call(self, inputs):
# inputs[0] = encoding data for the state.
batch_dim = tf.gather(tf.shape(inputs[0]), 0)
tiled_up_circuits = tf.repeat(self.empty_circuit, repeats=batch_dim)
tiled_up_thetas = tf.tile(self.theta, multiples=[batch_dim, 1])
tiled_up_inputs = tf.tile(inputs[0], multiples=[1, self.n_layers])
scaled_inputs = tf.einsum("i,ji->ji", self.lmbd, tiled_up_inputs)
squashed_inputs = tf.keras.layers.Activation(self.activation)(scaled_inputs)
joined_vars = tf.concat([tiled_up_thetas, squashed_inputs], axis=1)
joined_vars = tf.gather(joined_vars, self.indices, axis=1)
return self.computation_layer([tiled_up_circuits, joined_vars])
2. 使用 PQC 策略的策略梯度 RL
在本节中,您将实现 [1] 中提出的策略梯度算法。为此,您将首先在刚刚定义的 PQC 之外构建 softmax-VQC 策略(其中 VQC 代表变分量子电路)
\[ \pi_\theta(a|s) = \frac{e^{\beta \langle O_a \rangle_{s,\theta} } }{\sum_{a'} e^{\beta \langle O_{a'} \rangle_{s,\theta} } } \]
其中\(\langle O_a \rangle_{s,\theta}\) 是在 PQC 输出处测量的可观测量 \(O_a\)(每个动作一个)的期望值,\(\beta\) 是可调的逆温度参数。
你可以采用 [1] 中用于 CartPole 的相同可观测量,即作用于所有量子比特的全局 \(Z_0Z_1Z_2Z_3\) 泡利乘积,每个动作按动作特定权重加权。要实现泡利乘积的加权,可以使用一个额外的 tf.keras.layers.Layer,它存储动作特定权重,并将其乘法应用于期望值\(\langle Z_0Z_1Z_2Z_3 \rangle_{s,\theta}\)。
class Alternating(tf.keras.layers.Layer):
def __init__(self, output_dim):
super(Alternating, self).__init__()
self.w = tf.Variable(
initial_value=tf.constant([[(-1.)**i for i in range(output_dim)]]), dtype="float32",
trainable=True, name="obs-weights")
def call(self, inputs):
return tf.matmul(inputs, self.w)
准备 PQC 的定义
n_qubits = 4 # Dimension of the state vectors in CartPole
n_layers = 5 # Number of layers in the PQC
n_actions = 2 # Number of actions in CartPole
qubits = cirq.GridQubit.rect(1, n_qubits)
及其可观测量
ops = [cirq.Z(q) for q in qubits]
observables = [reduce((lambda x, y: x * y), ops)] # Z_0*Z_1*Z_2*Z_3
使用它定义一个 tf.keras.Model,它按顺序应用先前定义的 ReUploadingPQC 层,然后应用一个使用 Alternating 计算加权可观测量的后处理层,然后将其输入到 tf.keras.layers.Softmax 层,该层输出代理的 softmax-VQC 策略。
def generate_model_policy(qubits, n_layers, n_actions, beta, observables):
"""Generates a Keras model for a data re-uploading PQC policy."""
input_tensor = tf.keras.Input(shape=(len(qubits), ), dtype=tf.dtypes.float32, name='input')
re_uploading_pqc = ReUploadingPQC(qubits, n_layers, observables)([input_tensor])
process = tf.keras.Sequential([
Alternating(n_actions),
tf.keras.layers.Lambda(lambda x: x * beta),
tf.keras.layers.Softmax()
], name="observables-policy")
policy = process(re_uploading_pqc)
model = tf.keras.Model(inputs=[input_tensor], outputs=policy)
return model
model = generate_model_policy(qubits, n_layers, n_actions, 1.0, observables)
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
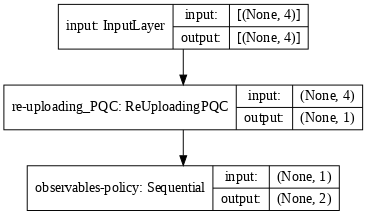
你现在可以使用基本的 REINFORCE 算法(参见 [1] 中的算法 1)在 CartPole-v1 上训练 PQC 策略。注意以下几点
- 由于缩放参数、变分角和可观测量权重使用不同的学习率进行训练,因此方便定义 3 个具有自己学习率的单独优化器,每个优化器更新这些参数组中的一个。
策略梯度 RL 中的损失函数为
\[ \mathcal{L}(\theta) = -\frac{1}{|\mathcal{B}|}\sum_{s_0,a_0,r_1,s_1,a_1, \ldots \in \mathcal{B} } \left(\sum_{t=0}^{H-1} \log(\pi_\theta(a_t|s_t)) \sum_{t'=1}^{H-t} \gamma^{t'} r_{t+t'} \right)\]
对于一批情节 \(\mathcal{B}\) 的情节 \((s_0,a_0,r_1,s_1,a_1, \ldots)\) 在遵循策略 \(\pi_\theta\) 的环境中的交互。这不同于具有固定目标值的监督学习损失,模型应适应该目标值,这使得不可能使用诸如 model.fit 之类的简单函数调用来训练策略。相反,使用 tf.GradientTape 允许跟踪涉及 PQC(即策略采样)的计算,并在交互期间存储它们对损失的贡献。在运行一批情节后,您可以对这些计算应用反向传播,以获得损失相对于 PQC 参数的梯度,并使用优化器更新策略模型。
首先定义一个函数,用于收集与环境交互的情节
def gather_episodes(state_bounds, n_actions, model, n_episodes, env_name):
"""Interact with environment in batched fashion."""
trajectories = [defaultdict(list) for _ in range(n_episodes)]
envs = [gym.make(env_name) for _ in range(n_episodes)]
done = [False for _ in range(n_episodes)]
states = [e.reset() for e in envs]
while not all(done):
unfinished_ids = [i for i in range(n_episodes) if not done[i]]
normalized_states = [s/state_bounds for i, s in enumerate(states) if not done[i]]
for i, state in zip(unfinished_ids, normalized_states):
trajectories[i]['states'].append(state)
# Compute policy for all unfinished envs in parallel
states = tf.convert_to_tensor(normalized_states)
action_probs = model([states])
# Store action and transition all environments to the next state
states = [None for i in range(n_episodes)]
for i, policy in zip(unfinished_ids, action_probs.numpy()):
action = np.random.choice(n_actions, p=policy)
states[i], reward, done[i], _ = envs[i].step(action)
trajectories[i]['actions'].append(action)
trajectories[i]['rewards'].append(reward)
return trajectories
以及一个函数,用于计算折扣回报 \(\sum_{t'=1}^{H-t} \gamma^{t'} r_{t+t'}\) 从情节中收集的奖励 \(r_t\)
def compute_returns(rewards_history, gamma):
"""Compute discounted returns with discount factor `gamma`."""
returns = []
discounted_sum = 0
for r in rewards_history[::-1]:
discounted_sum = r + gamma * discounted_sum
returns.insert(0, discounted_sum)
# Normalize them for faster and more stable learning
returns = np.array(returns)
returns = (returns - np.mean(returns)) / (np.std(returns) + 1e-8)
returns = returns.tolist()
return returns
定义超参数
state_bounds = np.array([2.4, 2.5, 0.21, 2.5])
gamma = 1
batch_size = 10
n_episodes = 1000
准备优化器
optimizer_in = tf.keras.optimizers.Adam(learning_rate=0.1, amsgrad=True)
optimizer_var = tf.keras.optimizers.Adam(learning_rate=0.01, amsgrad=True)
optimizer_out = tf.keras.optimizers.Adam(learning_rate=0.1, amsgrad=True)
# Assign the model parameters to each optimizer
w_in, w_var, w_out = 1, 0, 2
实现一个使用状态、动作和回报更新策略的函数
@tf.function
def reinforce_update(states, actions, returns, model):
states = tf.convert_to_tensor(states)
actions = tf.convert_to_tensor(actions)
returns = tf.convert_to_tensor(returns)
with tf.GradientTape() as tape:
tape.watch(model.trainable_variables)
logits = model(states)
p_actions = tf.gather_nd(logits, actions)
log_probs = tf.math.log(p_actions)
loss = tf.math.reduce_sum(-log_probs * returns) / batch_size
grads = tape.gradient(loss, model.trainable_variables)
for optimizer, w in zip([optimizer_in, optimizer_var, optimizer_out], [w_in, w_var, w_out]):
optimizer.apply_gradients([(grads[w], model.trainable_variables[w])])
现在实现代理的主要训练循环。
env_name = "CartPole-v1"
# Start training the agent
episode_reward_history = []
for batch in range(n_episodes // batch_size):
# Gather episodes
episodes = gather_episodes(state_bounds, n_actions, model, batch_size, env_name)
# Group states, actions and returns in numpy arrays
states = np.concatenate([ep['states'] for ep in episodes])
actions = np.concatenate([ep['actions'] for ep in episodes])
rewards = [ep['rewards'] for ep in episodes]
returns = np.concatenate([compute_returns(ep_rwds, gamma) for ep_rwds in rewards])
returns = np.array(returns, dtype=np.float32)
id_action_pairs = np.array([[i, a] for i, a in enumerate(actions)])
# Update model parameters.
reinforce_update(states, id_action_pairs, returns, model)
# Store collected rewards
for ep_rwds in rewards:
episode_reward_history.append(np.sum(ep_rwds))
avg_rewards = np.mean(episode_reward_history[-10:])
print('Finished episode', (batch + 1) * batch_size,
'Average rewards: ', avg_rewards)
if avg_rewards >= 500.0:
break
Finished episode 10 Average rewards: 22.3 Finished episode 20 Average rewards: 27.4 Finished episode 30 Average rewards: 24.7 Finished episode 40 Average rewards: 21.2 Finished episode 50 Average rewards: 33.9 Finished episode 60 Average rewards: 31.3 Finished episode 70 Average rewards: 37.3 Finished episode 80 Average rewards: 34.4 Finished episode 90 Average rewards: 58.4 Finished episode 100 Average rewards: 33.2 Finished episode 110 Average rewards: 67.9 Finished episode 120 Average rewards: 63.9 Finished episode 130 Average rewards: 83.5 Finished episode 140 Average rewards: 88.0 Finished episode 150 Average rewards: 142.9 Finished episode 160 Average rewards: 204.7 Finished episode 170 Average rewards: 138.1 Finished episode 180 Average rewards: 183.0 Finished episode 190 Average rewards: 196.0 Finished episode 200 Average rewards: 302.0 Finished episode 210 Average rewards: 374.4 Finished episode 220 Average rewards: 329.1 Finished episode 230 Average rewards: 307.8 Finished episode 240 Average rewards: 359.6 Finished episode 250 Average rewards: 400.7 Finished episode 260 Average rewards: 414.4 Finished episode 270 Average rewards: 394.9 Finished episode 280 Average rewards: 470.7 Finished episode 290 Average rewards: 459.7 Finished episode 300 Average rewards: 428.7 Finished episode 310 Average rewards: 500.0
绘制代理的学习历史
plt.figure(figsize=(10,5))
plt.plot(episode_reward_history)
plt.xlabel('Epsiode')
plt.ylabel('Collected rewards')
plt.show()
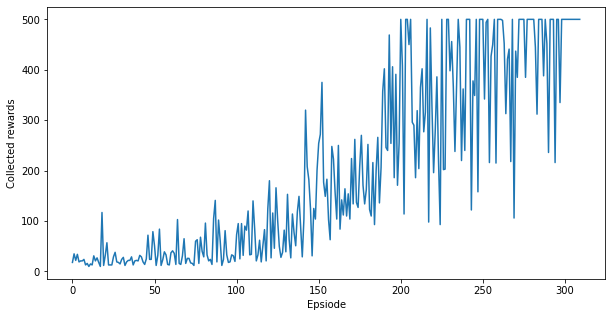
恭喜,您已在 Cartpole 上训练了量子策略梯度模型!上面的图表显示了代理在与环境交互期间每集收集的奖励。您应该看到,经过数百集后,代理的性能接近最优,即每集 500 个奖励。
您现在可以使用 env.render() 在示例情节中可视化代理的性能(仅当您的笔记本电脑可以显示时取消注释/运行以下单元格)
# from PIL import Image
# env = gym.make('CartPole-v1')
# state = env.reset()
# frames = []
# for t in range(500):
# im = Image.fromarray(env.render(mode='rgb_array'))
# frames.append(im)
# policy = model([tf.convert_to_tensor([state/state_bounds])])
# action = np.random.choice(n_actions, p=policy.numpy()[0])
# state, _, done, _ = env.step(action)
# if done:
# break
# env.close()
# frames[1].save('./images/gym_CartPole.gif',
# save_all=True, append_images=frames[2:], optimize=False, duration=40, loop=0)
3. 使用 PQC Q 函数逼近器的深度 Q 学习
在本节中,您将转到 [2] 中提出的深度 Q 学习算法的实现。与策略梯度方法相反,深度 Q 学习方法使用 PQC 来近似代理的 Q 函数。也就是说,PQC 定义了一个函数逼近器
\[ Q_\theta(s,a) = \langle O_a \rangle_{s,\theta} \]
其中 \(\langle O_a \rangle_{s,\theta}\) 是可观测值 \(O_a\) 的期望值(每个动作一个),在 PQC 的输出处测量。
这些 Q 值使用从 Q 学习中派生的损失函数进行更新
\[ \mathcal{L}(\theta) = \frac{1}{|\mathcal{B}|}\sum_{s,a,r,s' \in \mathcal{B} } \left(Q_\theta(s,a) - [r +\max_{a'} Q_{\theta'}(s',a')]\right)^2\]
对于一批 \(1\)- 步交互 \((s,a,r,s')\) 与环境,从重播记忆中采样,以及指定目标 PQC 的参数 \(\theta'\)(即,主 PQC 的副本,其参数在整个学习过程中会零星地从主 PQC 中复制)。
您可以采用 [2] 中用于 CartPole 的相同可观测值,即动作 \(0\) 的 \(Z_0Z_1\) 泡利积和动作 \(1\) 的 \(Z_2Z_3\) 泡利积。两个可观测值都重新缩放,因此它们的期望值在 \([0,1]\) 中,并按特定于动作的权重加权。要实现泡利积的重新缩放和加权,您可以再次定义一个额外的 tf.keras.layers.Layer,它存储特定于动作的权重,并将其乘法应用于期望值 \(\left(1+\langle Z_0Z_1 \rangle_{s,\theta}\right)/2\) 和 \(\left(1+\langle Z_2Z_3 \rangle_{s,\theta}\right)/2\)。
class Rescaling(tf.keras.layers.Layer):
def __init__(self, input_dim):
super(Rescaling, self).__init__()
self.input_dim = input_dim
self.w = tf.Variable(
initial_value=tf.ones(shape=(1,input_dim)), dtype="float32",
trainable=True, name="obs-weights")
def call(self, inputs):
return tf.math.multiply((inputs+1)/2, tf.repeat(self.w,repeats=tf.shape(inputs)[0],axis=0))
准备 PQC 及其可观测值的定义
n_qubits = 4 # Dimension of the state vectors in CartPole
n_layers = 5 # Number of layers in the PQC
n_actions = 2 # Number of actions in CartPole
qubits = cirq.GridQubit.rect(1, n_qubits)
ops = [cirq.Z(q) for q in qubits]
observables = [ops[0]*ops[1], ops[2]*ops[3]] # Z_0*Z_1 for action 0 and Z_2*Z_3 for action 1
定义一个 tf.keras.Model,它类似于 PQC 策略模型,构建一个 Q 函数逼近器,用于生成 Q 学习代理的主模型和目标模型。
def generate_model_Qlearning(qubits, n_layers, n_actions, observables, target):
"""Generates a Keras model for a data re-uploading PQC Q-function approximator."""
input_tensor = tf.keras.Input(shape=(len(qubits), ), dtype=tf.dtypes.float32, name='input')
re_uploading_pqc = ReUploadingPQC(qubits, n_layers, observables, activation='tanh')([input_tensor])
process = tf.keras.Sequential([Rescaling(len(observables))], name=target*"Target"+"Q-values")
Q_values = process(re_uploading_pqc)
model = tf.keras.Model(inputs=[input_tensor], outputs=Q_values)
return model
model = generate_model_Qlearning(qubits, n_layers, n_actions, observables, False)
model_target = generate_model_Qlearning(qubits, n_layers, n_actions, observables, True)
model_target.set_weights(model.get_weights())
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
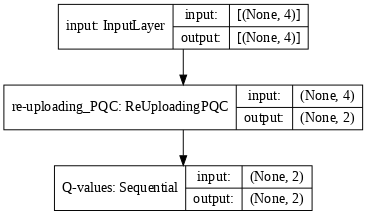
tf.keras.utils.plot_model(model_target, show_shapes=True, dpi=70)
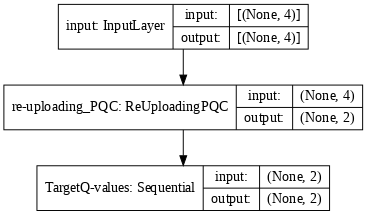
您现在可以实现深度 Q 学习算法,并在 CartPole-v1 环境中对其进行测试。对于代理的策略,您可以使用 \(\varepsilon\)- 贪婪策略
\[ \pi(a|s) = \begin{cases} \delta_{a,\text{argmax}_{a'} Q_\theta(s,a')}\quad \text{w.p.}\quad 1 - \varepsilon\\ \frac{1}{\text{num_actions} }\quad \quad \quad \quad \text{w.p.}\quad \varepsilon \end{cases} \]
其中 \(\varepsilon\) 在每次交互情节中乘法衰减。
首先定义一个在环境中执行交互步骤的函数
def interact_env(state, model, epsilon, n_actions, env):
# Preprocess state
state_array = np.array(state)
state = tf.convert_to_tensor([state_array])
# Sample action
coin = np.random.random()
if coin > epsilon:
q_vals = model([state])
action = int(tf.argmax(q_vals[0]).numpy())
else:
action = np.random.choice(n_actions)
# Apply sampled action in the environment, receive reward and next state
next_state, reward, done, _ = env.step(action)
interaction = {'state': state_array, 'action': action, 'next_state': next_state.copy(),
'reward': reward, 'done':np.float32(done)}
return interaction
以及一个使用一批交互更新 Q 函数的函数
@tf.function
def Q_learning_update(states, actions, rewards, next_states, done, model, gamma, n_actions):
states = tf.convert_to_tensor(states)
actions = tf.convert_to_tensor(actions)
rewards = tf.convert_to_tensor(rewards)
next_states = tf.convert_to_tensor(next_states)
done = tf.convert_to_tensor(done)
# Compute their target q_values and the masks on sampled actions
future_rewards = model_target([next_states])
target_q_values = rewards + (gamma * tf.reduce_max(future_rewards, axis=1)
* (1.0 - done))
masks = tf.one_hot(actions, n_actions)
# Train the model on the states and target Q-values
with tf.GradientTape() as tape:
tape.watch(model.trainable_variables)
q_values = model([states])
q_values_masked = tf.reduce_sum(tf.multiply(q_values, masks), axis=1)
loss = tf.keras.losses.Huber()(target_q_values, q_values_masked)
# Backpropagation
grads = tape.gradient(loss, model.trainable_variables)
for optimizer, w in zip([optimizer_in, optimizer_var, optimizer_out], [w_in, w_var, w_out]):
optimizer.apply_gradients([(grads[w], model.trainable_variables[w])])
定义超参数
gamma = 0.99
n_episodes = 2000
# Define replay memory
max_memory_length = 10000 # Maximum replay length
replay_memory = deque(maxlen=max_memory_length)
epsilon = 1.0 # Epsilon greedy parameter
epsilon_min = 0.01 # Minimum epsilon greedy parameter
decay_epsilon = 0.99 # Decay rate of epsilon greedy parameter
batch_size = 16
steps_per_update = 10 # Train the model every x steps
steps_per_target_update = 30 # Update the target model every x steps
准备优化器
optimizer_in = tf.keras.optimizers.Adam(learning_rate=0.001, amsgrad=True)
optimizer_var = tf.keras.optimizers.Adam(learning_rate=0.001, amsgrad=True)
optimizer_out = tf.keras.optimizers.Adam(learning_rate=0.1, amsgrad=True)
# Assign the model parameters to each optimizer
w_in, w_var, w_out = 1, 0, 2
现在实现代理的主要训练循环。
env = gym.make("CartPole-v1")
episode_reward_history = []
step_count = 0
for episode in range(n_episodes):
episode_reward = 0
state = env.reset()
while True:
# Interact with env
interaction = interact_env(state, model, epsilon, n_actions, env)
# Store interaction in the replay memory
replay_memory.append(interaction)
state = interaction['next_state']
episode_reward += interaction['reward']
step_count += 1
# Update model
if step_count % steps_per_update == 0:
# Sample a batch of interactions and update Q_function
training_batch = np.random.choice(replay_memory, size=batch_size)
Q_learning_update(np.asarray([x['state'] for x in training_batch]),
np.asarray([x['action'] for x in training_batch]),
np.asarray([x['reward'] for x in training_batch], dtype=np.float32),
np.asarray([x['next_state'] for x in training_batch]),
np.asarray([x['done'] for x in training_batch], dtype=np.float32),
model, gamma, n_actions)
# Update target model
if step_count % steps_per_target_update == 0:
model_target.set_weights(model.get_weights())
# Check if the episode is finished
if interaction['done']:
break
# Decay epsilon
epsilon = max(epsilon * decay_epsilon, epsilon_min)
episode_reward_history.append(episode_reward)
if (episode+1)%10 == 0:
avg_rewards = np.mean(episode_reward_history[-10:])
print("Episode {}/{}, average last 10 rewards {}".format(
episode+1, n_episodes, avg_rewards))
if avg_rewards >= 500.0:
break
Episode 10/2000, average last 10 rewards 22.1 Episode 20/2000, average last 10 rewards 27.9 Episode 30/2000, average last 10 rewards 31.5 Episode 40/2000, average last 10 rewards 23.3 Episode 50/2000, average last 10 rewards 25.4 Episode 60/2000, average last 10 rewards 19.7 Episode 70/2000, average last 10 rewards 12.5 Episode 80/2000, average last 10 rewards 11.7 Episode 90/2000, average last 10 rewards 14.9 Episode 100/2000, average last 10 rewards 15.3 Episode 110/2000, average last 10 rewards 14.6 Episode 120/2000, average last 10 rewards 20.4 Episode 130/2000, average last 10 rewards 14.2 Episode 140/2000, average last 10 rewards 21.6 Episode 150/2000, average last 10 rewards 30.4 Episode 160/2000, average last 10 rewards 27.6 Episode 170/2000, average last 10 rewards 18.5 Episode 180/2000, average last 10 rewards 30.6 Episode 190/2000, average last 10 rewards 12.2 Episode 200/2000, average last 10 rewards 27.2 Episode 210/2000, average last 10 rewards 27.2 Episode 220/2000, average last 10 rewards 15.3 Episode 230/2000, average last 10 rewards 128.4 Episode 240/2000, average last 10 rewards 68.3 Episode 250/2000, average last 10 rewards 44.0 Episode 260/2000, average last 10 rewards 119.8 Episode 270/2000, average last 10 rewards 135.3 Episode 280/2000, average last 10 rewards 90.6 Episode 290/2000, average last 10 rewards 120.9 Episode 300/2000, average last 10 rewards 125.3 Episode 310/2000, average last 10 rewards 141.7 Episode 320/2000, average last 10 rewards 144.7 Episode 330/2000, average last 10 rewards 165.7 Episode 340/2000, average last 10 rewards 26.1 Episode 350/2000, average last 10 rewards 9.7 Episode 360/2000, average last 10 rewards 9.6 Episode 370/2000, average last 10 rewards 9.7 Episode 380/2000, average last 10 rewards 9.4 Episode 390/2000, average last 10 rewards 11.3 Episode 400/2000, average last 10 rewards 11.6 Episode 410/2000, average last 10 rewards 165.4 Episode 420/2000, average last 10 rewards 170.5 Episode 430/2000, average last 10 rewards 25.1 Episode 440/2000, average last 10 rewards 74.1 Episode 450/2000, average last 10 rewards 214.7 Episode 460/2000, average last 10 rewards 139.1 Episode 470/2000, average last 10 rewards 265.1 Episode 480/2000, average last 10 rewards 296.7 Episode 490/2000, average last 10 rewards 101.7 Episode 500/2000, average last 10 rewards 146.6 Episode 510/2000, average last 10 rewards 325.6 Episode 520/2000, average last 10 rewards 45.9 Episode 530/2000, average last 10 rewards 263.5 Episode 540/2000, average last 10 rewards 223.3 Episode 550/2000, average last 10 rewards 73.1 Episode 560/2000, average last 10 rewards 115.0 Episode 570/2000, average last 10 rewards 148.3 Episode 580/2000, average last 10 rewards 41.6 Episode 590/2000, average last 10 rewards 266.7 Episode 600/2000, average last 10 rewards 275.2 Episode 610/2000, average last 10 rewards 253.9 Episode 620/2000, average last 10 rewards 282.2 Episode 630/2000, average last 10 rewards 348.3 Episode 640/2000, average last 10 rewards 162.2 Episode 650/2000, average last 10 rewards 276.0 Episode 660/2000, average last 10 rewards 234.6 Episode 670/2000, average last 10 rewards 187.4 Episode 680/2000, average last 10 rewards 285.0 Episode 690/2000, average last 10 rewards 362.8 Episode 700/2000, average last 10 rewards 316.0 Episode 710/2000, average last 10 rewards 436.0 Episode 720/2000, average last 10 rewards 366.1 Episode 730/2000, average last 10 rewards 305.0 Episode 740/2000, average last 10 rewards 273.2 Episode 750/2000, average last 10 rewards 236.8 Episode 760/2000, average last 10 rewards 260.2 Episode 770/2000, average last 10 rewards 443.9 Episode 780/2000, average last 10 rewards 494.2 Episode 790/2000, average last 10 rewards 333.1 Episode 800/2000, average last 10 rewards 367.1 Episode 810/2000, average last 10 rewards 317.8 Episode 820/2000, average last 10 rewards 396.6 Episode 830/2000, average last 10 rewards 494.1 Episode 840/2000, average last 10 rewards 500.0
绘制代理的学习历史
plt.figure(figsize=(10,5))
plt.plot(episode_reward_history)
plt.xlabel('Epsiode')
plt.ylabel('Collected rewards')
plt.show()
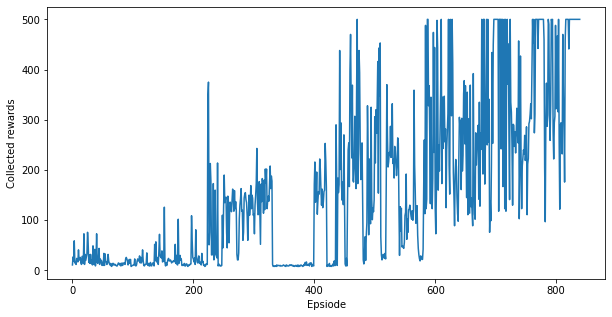
与上图类似,您应该看到在约 1000 个情节之后,代理的性能接近最优,即每集 500 个奖励。Q 学习代理的学习时间更长,因为 Q 函数是一个比策略更“丰富”的函数。
4. 练习
现在您已经训练了两种不同类型的模型,请尝试使用不同的环境(以及不同的量子比特和层数)。您还可以尝试将最后两节的 PQC 模型组合成一个actor-critic 代理。
