 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
本教程展示了经典神经网络如何学习纠正量子比特校准错误。它介绍了 Cirq,一个用于创建、编辑和调用噪声中级规模量子 (NISQ) 电路的 Python 框架,并演示了 Cirq 如何与 TensorFlow Quantum 交互。
设置
pip install tensorflow==2.15.0
安装 TensorFlow Quantum
pip install tensorflow-quantum==0.7.3
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
/tmpfs/tmp/ipykernel_11114/1875984233.py:2: DeprecationWarning: pkg_resources is deprecated as an API. See https://setuptools.pypa.io/en/latest/pkg_resources.html import importlib, pkg_resources <module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.9/site-packages/pkg_resources/__init__.py'>
现在导入 TensorFlow 和模块依赖项
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
2024-05-18 11:22:39.011840: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:9261] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2024-05-18 11:22:39.011885: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:607] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2024-05-18 11:22:39.013339: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1515] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered 2024-05-18 11:22:42.671821: E external/local_xla/xla/stream_executor/cuda/cuda_driver.cc:274] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. 基础知识
1.1 Cirq 和参数化量子电路
在探索 TensorFlow Quantum (TFQ) 之前,让我们先了解一些 Cirq 基础知识。Cirq 是 Google 的量子计算 Python 库。您可以使用它来定义电路,包括静态门和参数化门。
Cirq 使用 SymPy 符号来表示自由参数。
a, b = sympy.symbols('a b')
以下代码使用您的参数创建了一个双量子比特电路
# Create two qubits
q0, q1 = cirq.GridQubit.rect(1, 2)
# Create a circuit on these qubits using the parameters you created above.
circuit = cirq.Circuit(
cirq.rx(a).on(q0),
cirq.ry(b).on(q1), cirq.CNOT(q0, q1))
SVGCircuit(circuit)
findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found.
要评估电路,您可以使用 cirq.Simulator 接口。您可以通过传入 cirq.ParamResolver 对象,将电路中的自由参数替换为特定数字。以下代码计算参数化电路的原始状态向量输出
# Calculate a state vector with a=0.5 and b=-0.5.
resolver = cirq.ParamResolver({a: 0.5, b: -0.5})
output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state_vector
output_state_vector
array([ 0.9387913 +0.j , -0.23971277+0.j ,
0. +0.06120872j, 0. -0.23971277j], dtype=complex64)
状态向量在模拟之外无法直接访问(请注意上面的输出中的复数)。为了物理现实,您必须指定一个测量,它将状态向量转换为经典计算机可以理解的实数。Cirq 使用 泡利算符 \(\hat{X}\)、\(\hat{Y}\) 和 \(\hat{Z}\) 的组合来指定测量。例如,以下代码在您刚刚模拟的状态向量上测量 \(\hat{Z}_0\) 和 \(\frac{1}{2}\hat{Z}_0 + \hat{X}_1\)
z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_state_vector(output_state_vector, qubit_map).real
0.8775825500488281
z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_state_vector(output_state_vector, qubit_map).real
-0.04063427448272705
1.2 量子电路作为张量
TensorFlow Quantum (TFQ) 提供 tfq.convert_to_tensor,一个将 Cirq 对象转换为张量的函数。这使您可以将 Cirq 对象发送到我们的 量子层 和 量子操作。该函数可以对 Cirq 电路和 Cirq 泡利的列表或数组进行调用
# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])
print(circuit_tensor.shape)
print(circuit_tensor.dtype)
(1,) <dtype: 'string'>
这将 Cirq 对象编码为 tf.string 张量,tfq 操作会根据需要对其进行解码。
# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape
TensorShape([2])
1.3 批量电路模拟
TFQ 提供了计算期望值、样本和状态向量的方法。现在,让我们专注于期望值。
计算期望值的最高级别接口是 tfq.layers.Expectation 层,它是一个 tf.keras.Layer。在最简单的形式中,此层等效于在许多 cirq.ParamResolvers 上模拟参数化电路;但是,TFQ 允许遵循 TensorFlow 语义进行批处理,并且电路使用高效的 C++ 代码进行模拟。
创建一个批次的值来替换我们的 a 和 b 参数
batch_vals = np.array(np.random.uniform(0, 2 * np.pi, (5, 2)), dtype=float)
在 Cirq 中对参数值进行批处理电路执行需要循环
cirq_results = []
cirq_simulator = cirq.Simulator()
for vals in batch_vals:
resolver = cirq.ParamResolver({a: vals[0], b: vals[1]})
final_state_vector = cirq_simulator.simulate(circuit, resolver).final_state_vector
cirq_results.append(
[z0.expectation_from_state_vector(final_state_vector, {
q0: 0,
q1: 1
}).real])
print('cirq batch results: \n {}'.format(np.array(cirq_results)))
cirq batch results: [[ 0.91391081] [-0.99317902] [ 0.97061282] [-0.1768328 ] [-0.97718316]]
TFQ 中简化了相同的操作
tfq.layers.Expectation()(circuit,
symbol_names=[a, b],
symbol_values=batch_vals,
operators=z0)
<tf.Tensor: shape=(5, 1), dtype=float32, numpy=
array([[ 0.91391176],
[-0.99317884],
[ 0.97061294],
[-0.17683345],
[-0.977183 ]], dtype=float32)>
2. 混合量子经典优化
现在您已经了解了基础知识,让我们使用 TensorFlow Quantum 来构建一个混合量子经典神经网络。您将训练一个经典神经网络来控制单个量子比特。该控制将被优化以正确地将量子比特准备在 0 或 1 状态,克服模拟的系统校准错误。下图显示了架构
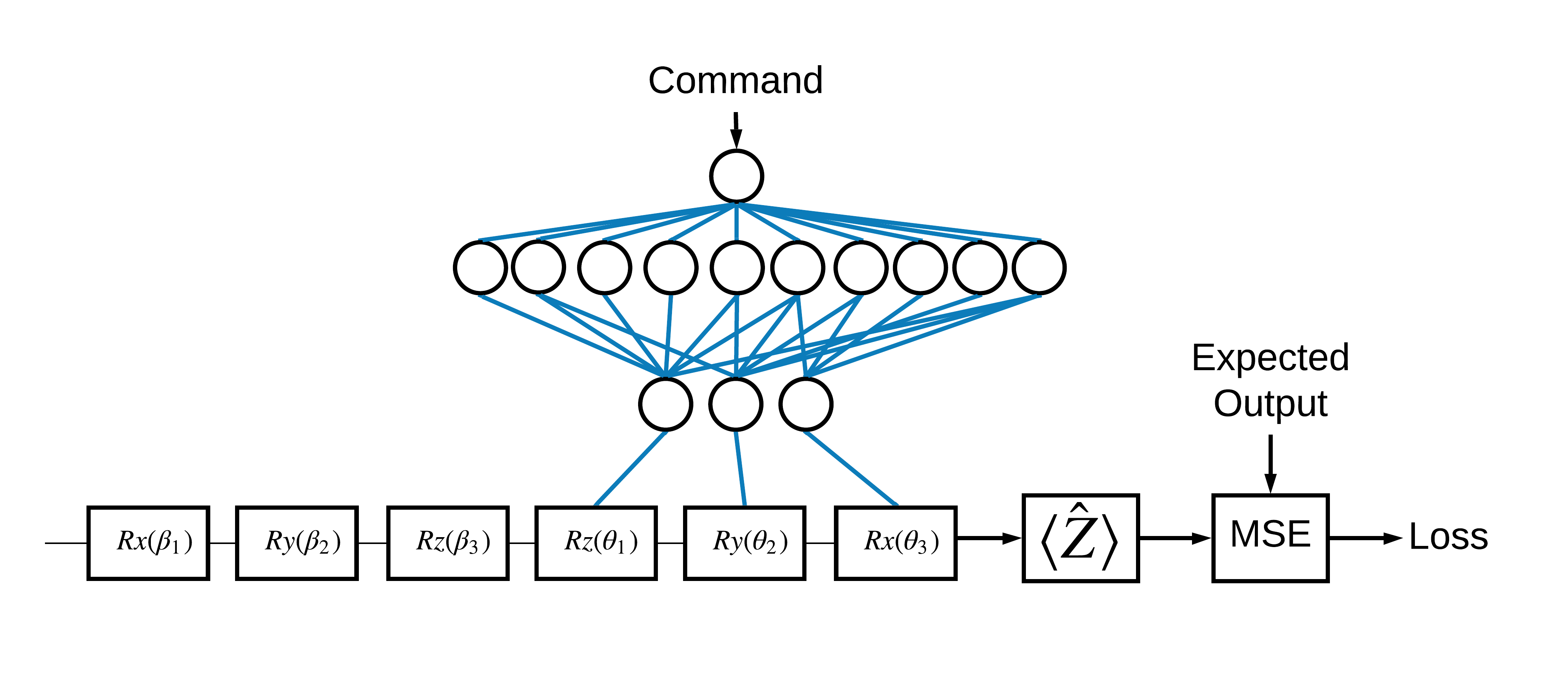
即使没有神经网络,这也是一个简单的解决问题,但主题与您可能使用 TFQ 解决的真实量子控制问题类似。它演示了使用 tfq.layers.ControlledPQC(参数化量子电路)层在 tf.keras.Model 中进行量子经典计算的端到端示例。
在本教程的实现中,此架构分为 3 部分
- 输入电路或数据点电路:前三个 \(R\) 门。
- 控制电路:其他三个 \(R\) 门。
- 控制器:设置控制电路参数的经典神经网络。
2.1 控制电路定义
定义一个可学习的单比特旋转,如上图所示。这将对应于我们的控制电路。
# Parameters that the classical NN will feed values into.
control_params = sympy.symbols('theta_1 theta_2 theta_3')
# Create the parameterized circuit.
qubit = cirq.GridQubit(0, 0)
model_circuit = cirq.Circuit(
cirq.rz(control_params[0])(qubit),
cirq.ry(control_params[1])(qubit),
cirq.rx(control_params[2])(qubit))
SVGCircuit(model_circuit)
findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found. findfont: Font family 'Arial' not found.
2.2 控制器
现在定义控制器网络
# The classical neural network layers.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
给定一批命令,控制器会输出一批控制电路的控制信号。
控制器是随机初始化的,因此这些输出目前没有用。
controller(tf.constant([[0.0],[1.0]])).numpy()
array([[ 0. , 0. , 0. ],
[-0.1500438 , -0.2821513 , -0.12589622]], dtype=float32)
2.3 将控制器连接到电路
使用 tfq 将控制器连接到受控电路,作为一个单独的 keras.Model。
有关此模型定义风格的更多信息,请参阅 Keras 函数式 API 指南。
首先定义模型的输入。
# This input is the simulated miscalibration that the model will learn to correct.
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.float32,
name='commands_input')
接下来,对这些输入应用操作,以定义计算。
dense_2 = controller(commands_input)
# TFQ layer for classically controlled circuits.
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = cirq.Z(qubit))
expectation = expectation_layer([circuits_input, dense_2])
现在将此计算打包为一个 tf.keras.Model。
# The full Keras model is built from our layers.
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=expectation)
网络架构由下图所示的模型图表示。将此模型图与架构图进行比较,以验证其正确性。
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
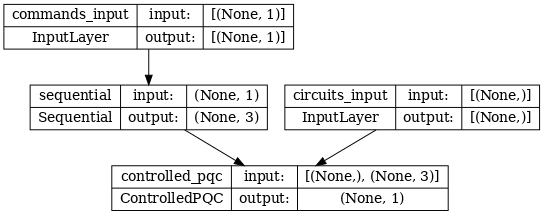
此模型接受两个输入:控制器的命令以及控制器试图纠正其输出的输入电路。
2.4 数据集
该模型试图输出每个命令的 \(\hat{Z}\) 的正确测量值。命令和正确值定义如下。
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired Z expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
这不是此任务的整个训练数据集。数据集中的每个数据点还需要一个输入电路。
2.4 输入电路定义
下面的输入电路定义了模型将学习纠正的随机误校准。
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit(
cirq.rx(random_rotations[0])(qubit),
cirq.ry(random_rotations[1])(qubit),
cirq.rz(random_rotations[2])(qubit)
)
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 2) # Make two copied of this circuit
该电路有两个副本,每个数据点一个。
datapoint_circuits.shape
TensorShape([2])
2.5 训练
定义好输入后,您可以测试运行 tfq 模型。
model([datapoint_circuits, commands]).numpy()
array([[-0.13725013],
[-0.13366866]], dtype=float32)
现在运行标准训练过程,以将这些值调整到 expected_outputs。
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss)
history = model.fit(x=[datapoint_circuits, commands],
y=expected_outputs,
epochs=30,
verbose=0)
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
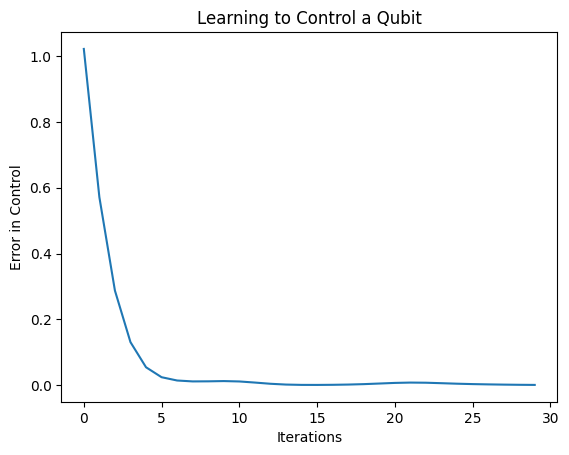
从该图可以看出,神经网络已经学会克服系统误校准。
2.6 验证输出
现在使用训练后的模型来纠正量子比特校准误差。使用 Cirq
def check_error(command_values, desired_values):
"""Based on the value in `command_value` see how well you could prepare
the full circuit to have `desired_value` when taking expectation w.r.t. Z."""
params_to_prepare_output = controller(command_values).numpy()
full_circuit = noisy_preparation + model_circuit
# Test how well you can prepare a state to get expectation the expectation
# value in `desired_values`
for index in [0, 1]:
state = cirq_simulator.simulate(
full_circuit,
{s:v for (s,v) in zip(control_params, params_to_prepare_output[index])}
).final_state_vector
expt = cirq.Z(qubit).expectation_from_state_vector(state, {qubit: 0}).real
print(f'For a desired output (expectation) of {desired_values[index]} with'
f' noisy preparation, the controller\nnetwork found the following '
f'values for theta: {params_to_prepare_output[index]}\nWhich gives an'
f' actual expectation of: {expt}\n')
check_error(commands, expected_outputs)
For a desired output (expectation) of [1.] with noisy preparation, the controller network found the following values for theta: [ 1.1249783 1.6464207 -2.502687 ] Which gives an actual expectation of: 0.9762285351753235 For a desired output (expectation) of [-1.] with noisy preparation, the controller network found the following values for theta: [-1.0330195 -1.6024671 0.2864415] Which gives an actual expectation of: -0.9853028655052185
训练期间损失函数的值提供了模型学习效果的粗略概念。损失越低,上述单元格中的期望值越接近 desired_values。如果您不太关心参数值,您可以始终使用 tfq 检查上述输出。
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.9762286],
[-0.9853029]], dtype=float32)>
3 学习准备不同算子的本征态
选择对应于 1 和 0 的 \(\pm \hat{Z}\) 本征态是任意的。您也可以同样地希望 1 对应于 \(+ \hat{Z}\) 本征态,而 0 对应于 \(-\hat{X}\) 本征态。实现此目的的一种方法是为每个命令指定不同的测量算子,如下图所示。
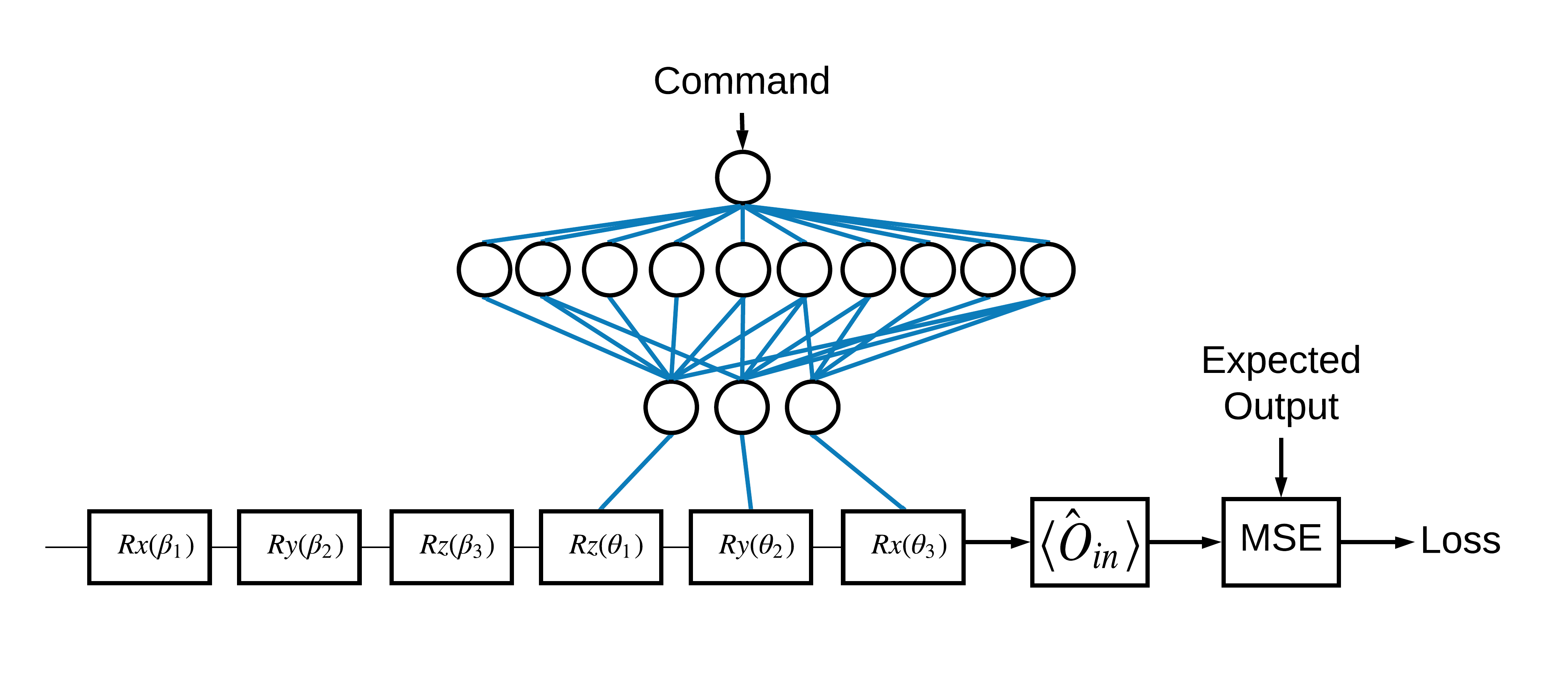
这需要使用 tfq.layers.Expectation。现在您的输入已扩展到包括三个对象:电路、命令和算子。输出仍然是期望值。
3.1 新模型定义
让我们看一下完成此任务的模型。
# Define inputs.
commands_input = tf.keras.layers.Input(shape=(1),
dtype=tf.dtypes.float32,
name='commands_input')
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.dtypes.string,
name='circuits_input')
operators_input = tf.keras.Input(shape=(1,),
dtype=tf.dtypes.string,
name='operators_input')
这是控制器网络。
# Define classical NN.
controller = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(3)
])
使用 tfq 将电路和控制器合并为一个单独的 keras.Model。
dense_2 = controller(commands_input)
# Since you aren't using a PQC or ControlledPQC you must append
# your model circuit onto the datapoint circuit tensor manually.
full_circuit = tfq.layers.AddCircuit()(circuits_input, append=model_circuit)
expectation_output = tfq.layers.Expectation()(full_circuit,
symbol_names=control_params,
symbol_values=dense_2,
operators=operators_input)
# Contruct your Keras model.
two_axis_control_model = tf.keras.Model(
inputs=[circuits_input, commands_input, operators_input],
outputs=[expectation_output])
3.2 数据集
现在您还将包括您希望为每个数据点测量的算子,这些数据点是您为 model_circuit 提供的。
# The operators to measure, for each command.
operator_data = tfq.convert_to_tensor([[cirq.X(qubit)], [cirq.Z(qubit)]])
# The command input values to the classical NN.
commands = np.array([[0], [1]], dtype=np.float32)
# The desired expectation value at output of quantum circuit.
expected_outputs = np.array([[1], [-1]], dtype=np.float32)
3.3 训练
现在您有了新的输入和输出,您可以使用 keras 再次进行训练。
optimizer = tf.keras.optimizers.Adam(learning_rate=0.05)
loss = tf.keras.losses.MeanSquaredError()
two_axis_control_model.compile(optimizer=optimizer, loss=loss)
history = two_axis_control_model.fit(
x=[datapoint_circuits, commands, operator_data],
y=expected_outputs,
epochs=30,
verbose=1)
Epoch 1/30 1/1 [==============================] - 0s 482ms/step - loss: 1.0518 Epoch 2/30 1/1 [==============================] - 0s 4ms/step - loss: 0.6841 Epoch 3/30 1/1 [==============================] - 0s 4ms/step - loss: 0.4386 Epoch 4/30 1/1 [==============================] - 0s 4ms/step - loss: 0.2500 Epoch 5/30 1/1 [==============================] - 0s 4ms/step - loss: 0.1179 Epoch 6/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0456 Epoch 7/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0172 Epoch 8/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0077 Epoch 9/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0035 Epoch 10/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0026 Epoch 11/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0060 Epoch 12/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0142 Epoch 13/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0256 Epoch 14/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0361 Epoch 15/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0430 Epoch 16/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0437 Epoch 17/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0359 Epoch 18/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0244 Epoch 19/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0146 Epoch 20/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0079 Epoch 21/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0038 Epoch 22/30 1/1 [==============================] - 0s 4ms/step - loss: 0.0016 Epoch 23/30 1/1 [==============================] - 0s 4ms/step - loss: 6.0264e-04 Epoch 24/30 1/1 [==============================] - 0s 4ms/step - loss: 1.8856e-04 Epoch 25/30 1/1 [==============================] - 0s 4ms/step - loss: 5.0837e-05 Epoch 26/30 1/1 [==============================] - 0s 4ms/step - loss: 1.5398e-05 Epoch 27/30 1/1 [==============================] - 0s 4ms/step - loss: 1.2333e-05 Epoch 28/30 1/1 [==============================] - 0s 4ms/step - loss: 2.5812e-05 Epoch 29/30 1/1 [==============================] - 0s 4ms/step - loss: 6.2401e-05 Epoch 30/30 1/1 [==============================] - 0s 4ms/step - loss: 1.3390e-04
plt.plot(history.history['loss'])
plt.title("Learning to Control a Qubit")
plt.xlabel("Iterations")
plt.ylabel("Error in Control")
plt.show()
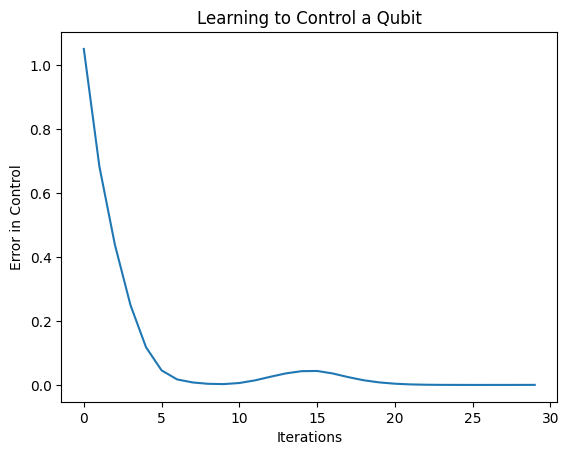
损失函数已降至零。
controller 可用作独立模型。调用控制器,并检查其对每个命令信号的响应。需要一些工作才能将这些输出与 random_rotations 的内容进行正确比较。
controller.predict(np.array([0,1]))
1/1 [==============================] - 0s 67ms/step
array([[ 1.6641312 , -0.06845868, -0.00440133],
[ 0.59975535, -1.9673042 , 1.7837791 ]], dtype=float32)
