 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
本教程基于 MNIST 教程中进行的比较,探讨了 Huang 等人 的最新研究,该研究展示了不同的数据集如何影响性能比较。在这项研究中,作者试图了解经典机器学习模型何时以及如何才能与量子模型一样好(或更好)地进行学习。该研究还通过精心制作的数据集展示了经典机器学习模型和量子机器学习模型之间的经验性能差异。你将
- 准备一个降维的 Fashion-MNIST 数据集。
- 使用量子电路重新标记数据集并计算投影量子核特征 (PQK)。
- 在重新标记的数据集上训练一个经典神经网络,并将其性能与可以访问 PQK 特征的模型进行比较。
设置
pip install tensorflow==2.15.0 tensorflow-quantum==0.7.3
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
1. 数据准备
你将首先准备 fashion-MNIST 数据集,以便在量子计算机上运行。
1.1 下载 fashion-MNIST
第一步是获取传统的 fashion-mnist 数据集。可以使用 tf.keras.datasets 模块来完成此操作。
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# Rescale the images from [0,255] to the [0.0,1.0] range.
x_train, x_test = x_train/255.0, x_test/255.0
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
Number of original training examples: 60000 Number of original test examples: 10000
过滤数据集以仅保留 T 恤/上衣和连衣裙,删除其他类别。同时将标签 y 转换为布尔值:0 为 True,3 为 False。
def filter_03(x, y):
keep = (y == 0) | (y == 3)
x, y = x[keep], y[keep]
y = y == 0
return x,y
x_train, y_train = filter_03(x_train, y_train)
x_test, y_test = filter_03(x_test, y_test)
print("Number of filtered training examples:", len(x_train))
print("Number of filtered test examples:", len(x_test))
Number of filtered training examples: 12000 Number of filtered test examples: 2000
print(y_train[0])
plt.imshow(x_train[0, :, :])
plt.colorbar()
True <matplotlib.colorbar.Colorbar at 0x7f6db42c3460>

1.2 缩小图像
与 MNIST 示例类似,你需要缩小这些图像,以便在当前量子计算机的边界内。但这次,你将使用 PCA 变换来降低维度,而不是 tf.image.resize 操作。
def truncate_x(x_train, x_test, n_components=10):
"""Perform PCA on image dataset keeping the top `n_components` components."""
n_points_train = tf.gather(tf.shape(x_train), 0)
n_points_test = tf.gather(tf.shape(x_test), 0)
# Flatten to 1D
x_train = tf.reshape(x_train, [n_points_train, -1])
x_test = tf.reshape(x_test, [n_points_test, -1])
# Normalize.
feature_mean = tf.reduce_mean(x_train, axis=0)
x_train_normalized = x_train - feature_mean
x_test_normalized = x_test - feature_mean
# Truncate.
e_values, e_vectors = tf.linalg.eigh(
tf.einsum('ji,jk->ik', x_train_normalized, x_train_normalized))
return tf.einsum('ij,jk->ik', x_train_normalized, e_vectors[:,-n_components:]), \
tf.einsum('ij,jk->ik', x_test_normalized, e_vectors[:, -n_components:])
DATASET_DIM = 10
x_train, x_test = truncate_x(x_train, x_test, n_components=DATASET_DIM)
print(f'New datapoint dimension:', len(x_train[0]))
New datapoint dimension: 10
最后一步是将数据集的大小减小到仅 1000 个训练数据点和 200 个测试数据点。
N_TRAIN = 1000
N_TEST = 200
x_train, x_test = x_train[:N_TRAIN], x_test[:N_TEST]
y_train, y_test = y_train[:N_TRAIN], y_test[:N_TEST]
print("New number of training examples:", len(x_train))
print("New number of test examples:", len(x_test))
New number of training examples: 1000 New number of test examples: 200
2. 重新标记和计算 PQK 特征
你现在将准备一个“僵化的”量子数据集,方法是合并量子组件并重新标记上面创建的截断 fashion-MNIST 数据集。为了在量子方法和经典方法之间获得最大的分离,你将首先准备 PQK 特征,然后根据其值重新标记输出。
2.1 量子编码和 PQK 特征
你将基于 x_train、y_train、x_test 和 y_test 创建一组新特征,定义为所有量子比特上的 1-RDM
\(V(x_{\text{train} } / n_{\text{trotter} }) ^ {n_{\text{trotter} } } U_{\text{1qb} } | 0 \rangle\)
其中 \(U_\text{1qb}\) 是单量子比特旋转壁,\(V(\hat{\theta}) = e^{-i\sum_i \hat{\theta_i} (X_i X_{i+1} + Y_i Y_{i+1} + Z_i Z_{i+1})}\)
首先,你可以生成单量子比特旋转壁
def single_qubit_wall(qubits, rotations):
"""Prepare a single qubit X,Y,Z rotation wall on `qubits`."""
wall_circuit = cirq.Circuit()
for i, qubit in enumerate(qubits):
for j, gate in enumerate([cirq.X, cirq.Y, cirq.Z]):
wall_circuit.append(gate(qubit) ** rotations[i][j])
return wall_circuit
你可以通过查看电路快速验证这一点
SVGCircuit(single_qubit_wall(
cirq.GridQubit.rect(1,4), np.random.uniform(size=(4, 3))))
接下来,你可以借助 tfq.util.exponential 准备 \(V(\hat{\theta})\),它可以对任何可交换的 cirq.PauliSum 对象求指数
def v_theta(qubits):
"""Prepares a circuit that generates V(\theta)."""
ref_paulis = [
cirq.X(q0) * cirq.X(q1) + \
cirq.Y(q0) * cirq.Y(q1) + \
cirq.Z(q0) * cirq.Z(q1) for q0, q1 in zip(qubits, qubits[1:])
]
exp_symbols = list(sympy.symbols('ref_0:'+str(len(ref_paulis))))
return tfq.util.exponential(ref_paulis, exp_symbols), exp_symbols
通过查看这个电路可能有点难以验证,但你仍然可以检查一个双量子比特案例来了解发生了什么
test_circuit, test_symbols = v_theta(cirq.GridQubit.rect(1, 2))
print(f'Symbols found in circuit:{test_symbols}')
SVGCircuit(test_circuit)
Symbols found in circuit:[ref_0]
现在,你拥有了将完整编码电路组合在一起所需的所有构建模块
def prepare_pqk_circuits(qubits, classical_source, n_trotter=10):
"""Prepare the pqk feature circuits around a dataset."""
n_qubits = len(qubits)
n_points = len(classical_source)
# Prepare random single qubit rotation wall.
random_rots = np.random.uniform(-2, 2, size=(n_qubits, 3))
initial_U = single_qubit_wall(qubits, random_rots)
# Prepare parametrized V
V_circuit, symbols = v_theta(qubits)
exp_circuit = cirq.Circuit(V_circuit for t in range(n_trotter))
# Convert to `tf.Tensor`
initial_U_tensor = tfq.convert_to_tensor([initial_U])
initial_U_splat = tf.tile(initial_U_tensor, [n_points])
full_circuits = tfq.layers.AddCircuit()(
initial_U_splat, append=exp_circuit)
# Replace placeholders in circuits with values from `classical_source`.
return tfq.resolve_parameters(
full_circuits, tf.convert_to_tensor([str(x) for x in symbols]),
tf.convert_to_tensor(classical_source*(n_qubits/3)/n_trotter))
选择一些量子比特并准备数据编码电路
qubits = cirq.GridQubit.rect(1, DATASET_DIM + 1)
q_x_train_circuits = prepare_pqk_circuits(qubits, x_train)
q_x_test_circuits = prepare_pqk_circuits(qubits, x_test)
接下来,根据上述数据集电路的 1-RDM 计算 PQK 特征,并将结果存储在 rdm 中,这是一个 tf.Tensor,形状为 [n_points, n_qubits, 3]。其中 rdm[i][j][k] 中的条目 = \(\langle \psi_i | OP^k_j | \psi_i \rangle\),其中 i 索引数据点,j 索引量子比特,k 索引 \(\lbrace \hat{X}, \hat{Y}, \hat{Z} \rbrace\) 。
def get_pqk_features(qubits, data_batch):
"""Get PQK features based on above construction."""
ops = [[cirq.X(q), cirq.Y(q), cirq.Z(q)] for q in qubits]
ops_tensor = tf.expand_dims(tf.reshape(tfq.convert_to_tensor(ops), -1), 0)
batch_dim = tf.gather(tf.shape(data_batch), 0)
ops_splat = tf.tile(ops_tensor, [batch_dim, 1])
exp_vals = tfq.layers.Expectation()(data_batch, operators=ops_splat)
rdm = tf.reshape(exp_vals, [batch_dim, len(qubits), -1])
return rdm
x_train_pqk = get_pqk_features(qubits, q_x_train_circuits)
x_test_pqk = get_pqk_features(qubits, q_x_test_circuits)
print('New PQK training dataset has shape:', x_train_pqk.shape)
print('New PQK testing dataset has shape:', x_test_pqk.shape)
New PQK training dataset has shape: (1000, 11, 3) New PQK testing dataset has shape: (200, 11, 3)
2.2 基于 PQK 特征重新标记
现在您已在 x_train_pqk 和 x_test_pqk 中拥有这些量子生成特征,是时候重新标记数据集了。为了实现量子和经典性能之间的最大分离,您可以根据在 x_train_pqk 和 x_test_pqk 中找到的频谱信息重新标记数据集。
def compute_kernel_matrix(vecs, gamma):
"""Computes d[i][j] = e^ -gamma * (vecs[i] - vecs[j]) ** 2 """
scaled_gamma = gamma / (
tf.cast(tf.gather(tf.shape(vecs), 1), tf.float32) * tf.math.reduce_std(vecs))
return scaled_gamma * tf.einsum('ijk->ij',(vecs[:,None,:] - vecs) ** 2)
def get_spectrum(datapoints, gamma=1.0):
"""Compute the eigenvalues and eigenvectors of the kernel of datapoints."""
KC_qs = compute_kernel_matrix(datapoints, gamma)
S, V = tf.linalg.eigh(KC_qs)
S = tf.math.abs(S)
return S, V
S_pqk, V_pqk = get_spectrum(
tf.reshape(tf.concat([x_train_pqk, x_test_pqk], 0), [-1, len(qubits) * 3]))
S_original, V_original = get_spectrum(
tf.cast(tf.concat([x_train, x_test], 0), tf.float32), gamma=0.005)
print('Eigenvectors of pqk kernel matrix:', V_pqk)
print('Eigenvectors of original kernel matrix:', V_original)
Eigenvectors of pqk kernel matrix: tf.Tensor( [[-2.09569391e-02 1.05973557e-02 2.16634180e-02 ... 2.80352887e-02 1.55521873e-02 2.82677952e-02] [-2.29303762e-02 4.66355234e-02 7.91163836e-03 ... -6.14174758e-04 -7.07804322e-01 2.85902526e-02] [-1.77853629e-02 -3.00758495e-03 -2.55225878e-02 ... -2.40783971e-02 2.11018627e-03 2.69009806e-02] ... [ 6.05797209e-02 1.32483775e-02 2.69536003e-02 ... -1.38843581e-02 3.05043962e-02 3.85345481e-02] [ 6.33309558e-02 -3.04112374e-03 9.77444276e-03 ... 7.48321265e-02 3.42793856e-03 3.67484428e-02] [ 5.86028099e-02 5.84433973e-03 2.64811981e-03 ... 2.82612257e-02 -3.80136147e-02 3.29943895e-02]], shape=(1200, 1200), dtype=float32) Eigenvectors of original kernel matrix: tf.Tensor( [[ 0.03835681 0.0283473 -0.01169789 ... 0.02343717 0.0211248 0.03206972] [-0.04018159 0.00888097 -0.01388255 ... 0.00582427 0.717551 0.02881948] [-0.0166719 0.01350376 -0.03663862 ... 0.02467175 -0.00415936 0.02195409] ... [-0.03015648 -0.01671632 -0.01603392 ... 0.00100583 -0.00261221 0.02365689] [ 0.0039777 -0.04998879 -0.00528336 ... 0.01560401 -0.04330755 0.02782002] [-0.01665728 -0.00818616 -0.0432341 ... 0.00088256 0.00927396 0.01875088]], shape=(1200, 1200), dtype=float32)
现在您拥有重新标记数据集所需的一切!现在您可以参考流程图,以更好地了解如何在重新标记数据集时最大化性能分离
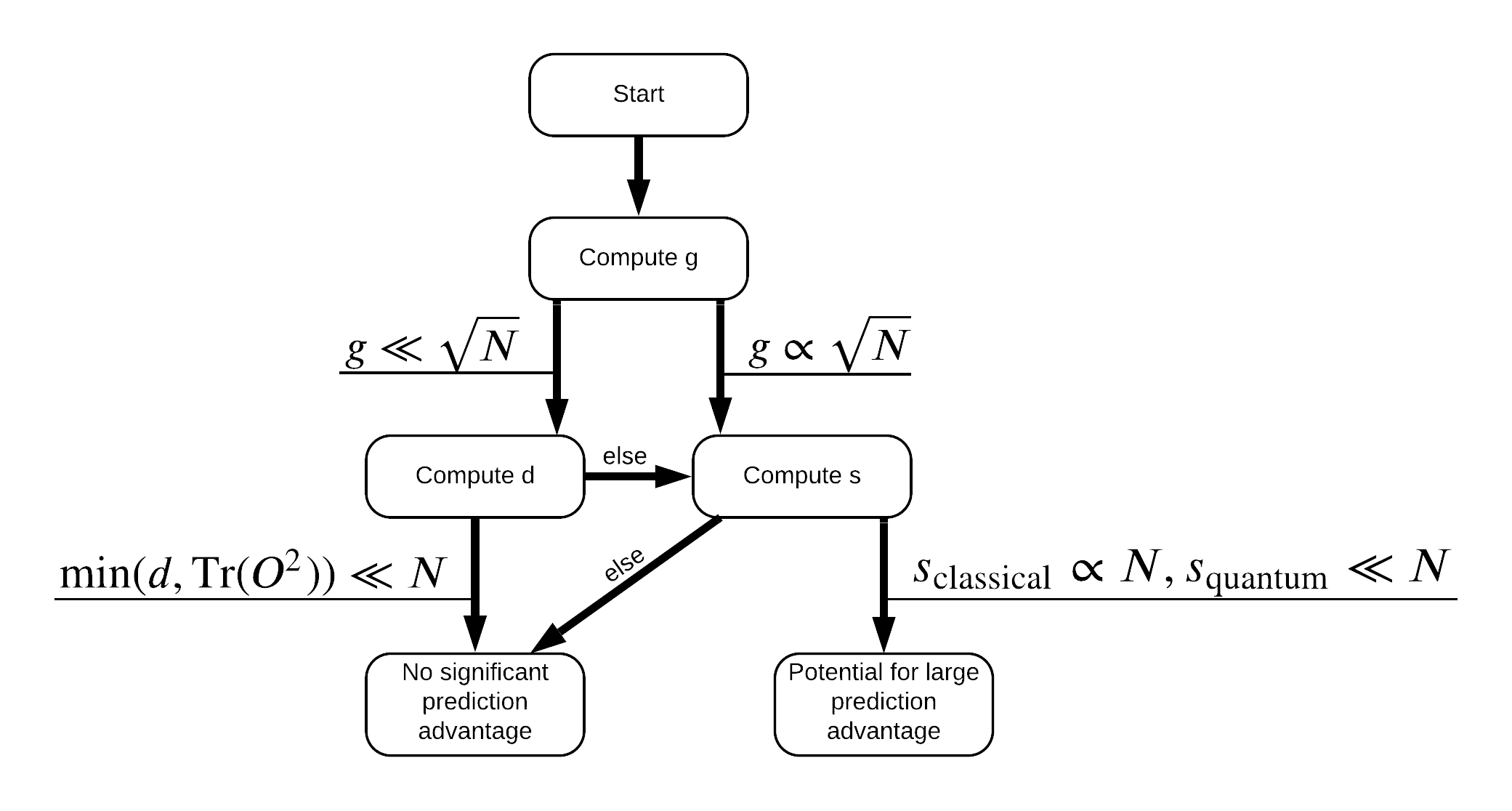
为了最大化量子模型和经典模型之间的分离,您将尝试使用 S_pqk, V_pqk 和 S_original, V_original 最大化原始数据集和 PQK 特征核矩阵 \(g(K_1 || K_2) = \sqrt{ || \sqrt{K_2} K_1^{-1} \sqrt{K_2} || _\infty}\) 之间的几何差异。较大的 \(g\) 值确保您最初在流程图中向右移动,朝量子情况下的预测优势迈进。
def get_stilted_dataset(S, V, S_2, V_2, lambdav=1.1):
"""Prepare new labels that maximize geometric distance between kernels."""
S_diag = tf.linalg.diag(S ** 0.5)
S_2_diag = tf.linalg.diag(S_2 / (S_2 + lambdav) ** 2)
scaling = S_diag @ tf.transpose(V) @ \
V_2 @ S_2_diag @ tf.transpose(V_2) @ \
V @ S_diag
# Generate new lables using the largest eigenvector.
_, vecs = tf.linalg.eig(scaling)
new_labels = tf.math.real(
tf.einsum('ij,j->i', tf.cast(V @ S_diag, tf.complex64), vecs[-1])).numpy()
# Create new labels and add some small amount of noise.
final_y = new_labels > np.median(new_labels)
noisy_y = (final_y ^ (np.random.uniform(size=final_y.shape) > 0.95))
return noisy_y
y_relabel = get_stilted_dataset(S_pqk, V_pqk, S_original, V_original)
y_train_new, y_test_new = y_relabel[:N_TRAIN], y_relabel[N_TRAIN:]
3. 比较模型
现在您已准备就绪数据集,是时候比较模型性能了。您将创建两个小型前馈神经网络,并在它们可以访问 x_train_pqk 中的 PQK 特征时比较性能。
3.1 创建 PQK 增强模型
使用标准 tf.keras 库功能,您现在可以在 x_train_pqk 和 y_train_new 数据点上创建和训练模型
#docs_infra: no_execute
def create_pqk_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[len(qubits) * 3,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
pqk_model = create_pqk_model()
pqk_model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.003),
metrics=['accuracy'])
pqk_model.summary()
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 32) 1088 _________________________________________________________________ dense_1 (Dense) (None, 16) 528 _________________________________________________________________ dense_2 (Dense) (None, 1) 17 ================================================================= Total params: 1,633 Trainable params: 1,633 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
pqk_history = pqk_model.fit(tf.reshape(x_train_pqk, [N_TRAIN, -1]),
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(tf.reshape(x_test_pqk, [N_TEST, -1]), y_test_new))
3.2 创建经典模型
与上述代码类似,您现在还可以创建一个经典模型,该模型无法访问您的人为数据集中的 PQK 特征。可以使用 x_train 和 y_label_new 训练此模型。
#docs_infra: no_execute
def create_fair_classical_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation='sigmoid', input_shape=[DATASET_DIM,]))
model.add(tf.keras.layers.Dense(16, activation='sigmoid'))
model.add(tf.keras.layers.Dense(1))
return model
model = create_fair_classical_model()
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(learning_rate=0.03),
metrics=['accuracy'])
model.summary()
Model: "sequential_1" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_3 (Dense) (None, 32) 352 _________________________________________________________________ dense_4 (Dense) (None, 16) 528 _________________________________________________________________ dense_5 (Dense) (None, 1) 17 ================================================================= Total params: 897 Trainable params: 897 Non-trainable params: 0 _________________________________________________________________
#docs_infra: no_execute
classical_history = model.fit(x_train,
y_train_new,
batch_size=32,
epochs=1000,
verbose=0,
validation_data=(x_test, y_test_new))
3.3 比较性能
现在您已经训练了这两个模型,您可以快速绘制这两个模型在验证数据中的性能差距。通常,这两个模型在训练数据上都能达到 > 0.9 的准确度。然而,在验证数据上,很明显只有 PQK 特征中的信息足以使模型很好地推广到看不见的实例。
#docs_infra: no_execute
plt.figure(figsize=(10,5))
plt.plot(classical_history.history['accuracy'], label='accuracy_classical')
plt.plot(classical_history.history['val_accuracy'], label='val_accuracy_classical')
plt.plot(pqk_history.history['accuracy'], label='accuracy_quantum')
plt.plot(pqk_history.history['val_accuracy'], label='val_accuracy_quantum')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x7f6d846ecee0>
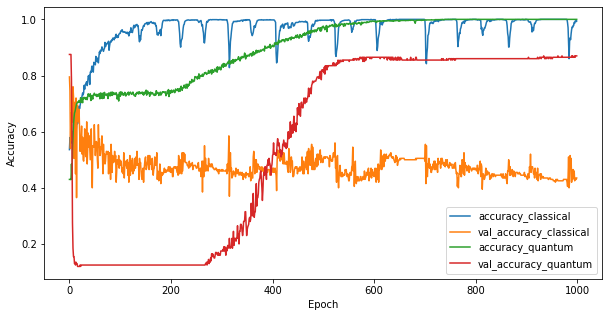
4. 重要结论
您可以从这个和 MNIST 实验中得出几个重要的结论
当今的量子模型不太可能在经典数据上击败经典模型性能。尤其是在当今拥有超过一百万个数据点的经典数据集上。
仅仅因为数据可能来自难以经典模拟的量子电路,并不一定意味着这些数据对于经典模型来说难以学习。
存在对量子模型来说易于学习而对经典模型来说难以学习的数据集(最终本质上是量子),无论所用模型架构或训练算法如何。
