在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
噪声存在于现代量子计算机中。量子比特容易受到周围环境、不完美的制造、TLS,有时甚至 伽马射线 的干扰。在大规模纠错实现之前,当今的算法必须能够在存在噪声的情况下保持功能。这使得在噪声下测试算法成为验证量子算法/模型将在当今量子计算机上运行的重要步骤。
在本教程中,您将通过高级 tfq.layers API 了解 TFQ 中噪声电路模拟的基础知识。
设置
pip install tensorflow==2.15.0 tensorflow-quantum==0.7.3
pip install -q git+https://github.com/tensorflow/docs
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
/tmpfs/tmp/ipykernel_32316/1875984233.py:2: DeprecationWarning: pkg_resources is deprecated as an API. See https://setuptools.pypa.io/en/latest/pkg_resources.html import importlib, pkg_resources <module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.9/site-packages/pkg_resources/__init__.py'>
import random
import cirq
import sympy
import tensorflow_quantum as tfq
import tensorflow as tf
import numpy as np
# Plotting
import matplotlib.pyplot as plt
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
2024-05-18 11:48:47.699511: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:9261] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2024-05-18 11:48:47.699552: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:607] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2024-05-18 11:48:47.701066: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1515] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered 2024-05-18 11:48:49.731639: E external/local_xla/xla/stream_executor/cuda/cuda_driver.cc:274] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. 了解量子噪声
1.1 基本电路噪声
量子计算机上的噪声会影响您能够从中测量的比特串样本。您可以开始思考这一点的一种直观方式是,噪声量子计算机会在随机位置“插入”、“删除”或“替换”门,如下图所示
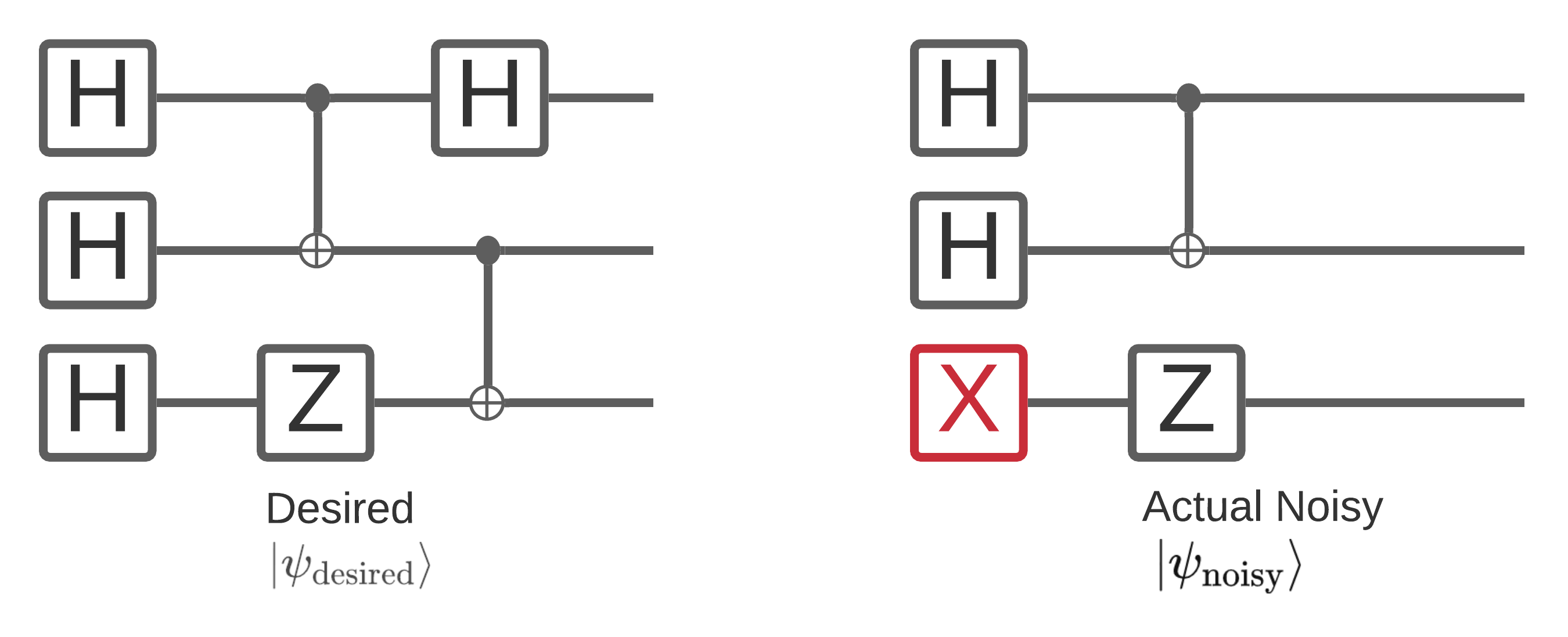
基于这种直觉,在处理噪声时,您不再使用单个纯态 \(|\psi \rangle\),而是处理所需电路的所有可能噪声实现的合集:\(\rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |\) 。其中 \(p_j\) 给出了系统处于 \(|\psi_j \rangle\) 的概率。
重新审视上图,如果我们事先知道 90% 的时间我们的系统执行完美,或者 10% 的时间仅出现这种一种故障模式,那么我们的合集将是
\(\rho = 0.9 |\psi_\text{desired} \rangle \langle \psi_\text{desired}| + 0.1 |\psi_\text{noisy} \rangle \langle \psi_\text{noisy}| \)
如果我们的电路出现错误的方式不止一种,那么集合\(\rho\)将包含不止两个项(每个项对应可能发生的一种新的噪声实现)。\(\rho\)被称为描述噪声系统的密度矩阵。
1.2 使用通道对电路噪声进行建模
不幸的是,在实践中几乎不可能知道电路可能出错的所有方式及其确切概率。你可以做出的一个简化假设是,在电路中的每个操作之后,都会出现某种通道,它大致描述了该操作可能如何出错。你可以快速创建一个带有噪声的电路
def x_circuit(qubits):
"""Produces an X wall circuit on `qubits`."""
return cirq.Circuit(cirq.X.on_each(*qubits))
def make_noisy(circuit, p):
"""Add a depolarization channel to all qubits in `circuit` before measurement."""
return circuit + cirq.Circuit(cirq.depolarize(p).on_each(*circuit.all_qubits()))
my_qubits = cirq.GridQubit.rect(1, 2)
my_circuit = x_circuit(my_qubits)
my_noisy_circuit = make_noisy(my_circuit, 0.5)
my_circuit
my_noisy_circuit
你可以使用以下命令检查无噪声密度矩阵\(\rho\)
rho = cirq.final_density_matrix(my_circuit)
np.round(rho, 3)
array([[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j]], dtype=complex64)
使用以下命令检查噪声密度矩阵\(\rho\)
rho = cirq.final_density_matrix(my_noisy_circuit)
np.round(rho, 3)
array([[0.111+0.j, 0. +0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0.222+0.j, 0. +0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0.222+0.j, 0. +0.j],
[0. +0.j, 0. +0.j, 0. +0.j, 0.444+0.j]], dtype=complex64)
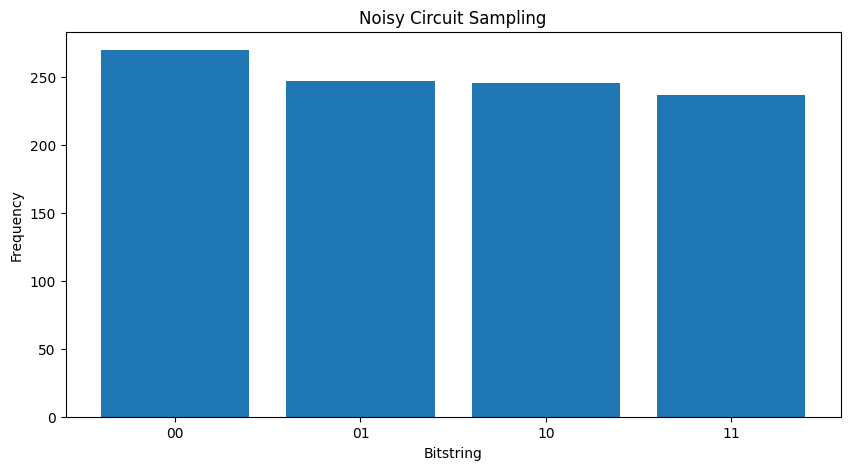
通过比较两个不同的\( \rho \),你可以看到噪声影响了状态的振幅(以及随后的采样概率)。在无噪声情况下,你总是期望采样\( |11\rangle \)状态。但在噪声状态下,现在还有非零概率采样\( |00\rangle \)或\( |01\rangle \)或\( |10\rangle \)
"""Sample from my_noisy_circuit."""
def plot_samples(circuit):
samples = cirq.sample(circuit + cirq.measure(*circuit.all_qubits(), key='bits'), repetitions=1000)
freqs, _ = np.histogram(samples.data['bits'], bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
plot_samples(my_noisy_circuit)
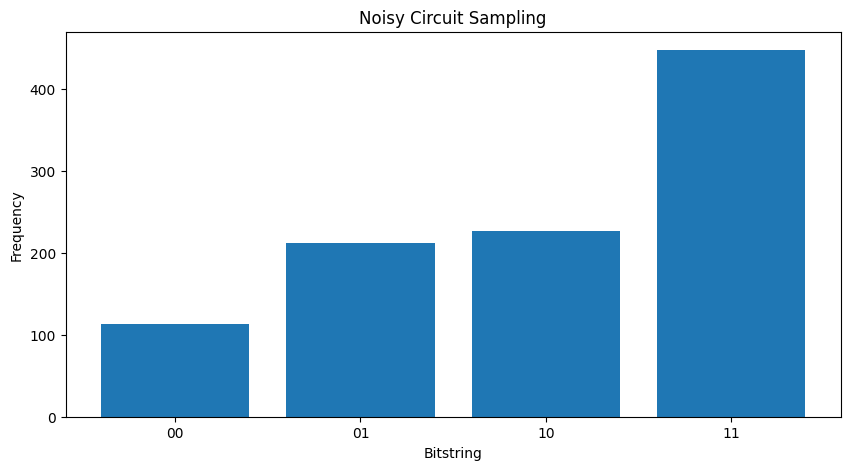
在没有噪声的情况下,你将始终得到\(|11\rangle\)
"""Sample from my_circuit."""
plot_samples(my_circuit)
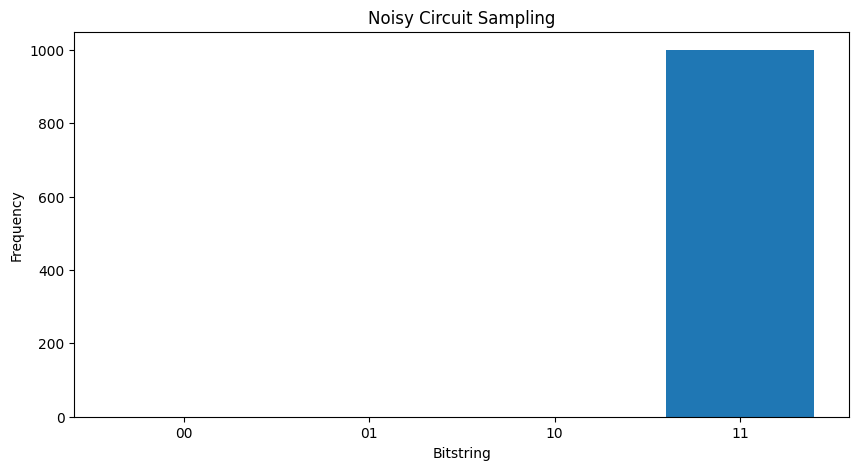
如果你进一步增加噪声,将越来越难以将期望的行为(采样\(|11\rangle\))与噪声区分开来
my_really_noisy_circuit = make_noisy(my_circuit, 0.75)
plot_samples(my_really_noisy_circuit)
2. TFQ 中的基本噪声
通过了解噪声如何影响电路执行,你可以探索噪声在 TFQ 中的工作原理。TensorFlow Quantum 使用基于蒙特卡罗/轨迹的模拟作为密度矩阵模拟的替代方案。这是因为密度矩阵模拟的内存复杂性限制了大型模拟,使其使用传统全密度矩阵模拟方法小于等于 20 个量子比特。蒙特卡罗/轨迹用时间成本换取了内存成本。backend='noisy' 选项可用于所有 tfq.layers.Sample、tfq.layers.SampledExpectation 和 tfq.layers.Expectation(在 Expectation 的情况下,这确实添加了一个必需的 repetitions 参数)。
2.1 TFQ 中的噪声采样
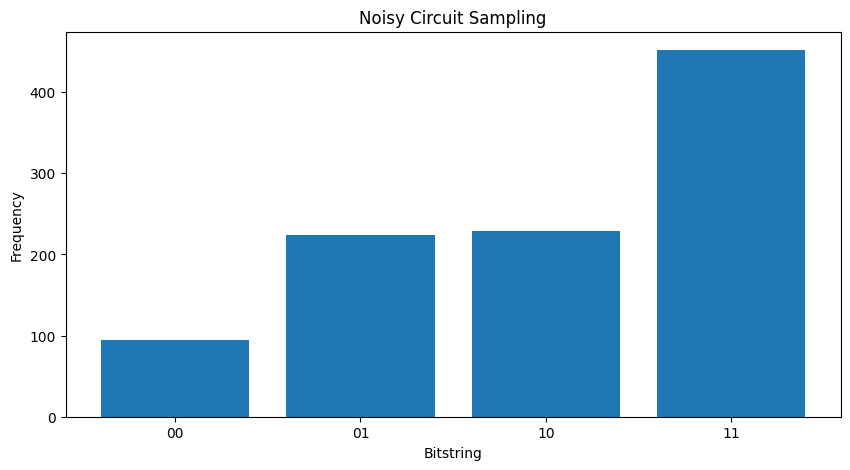
要使用 TFQ 和轨迹模拟重新创建上述绘图,你可以使用 tfq.layers.Sample
"""Draw bitstring samples from `my_noisy_circuit`"""
bitstrings = tfq.layers.Sample(backend='noisy')(my_noisy_circuit, repetitions=1000)
numeric_values = np.einsum('ijk,k->ij', bitstrings.to_tensor().numpy(), [1, 2])[0]
freqs, _ = np.histogram(numeric_values, bins=[i+0.01 for i in range(-1,2** len(my_qubits))])
plt.figure(figsize=(10,5))
plt.title('Noisy Circuit Sampling')
plt.xlabel('Bitstring')
plt.ylabel('Frequency')
plt.bar([i for i in range(2** len(my_qubits))], freqs, tick_label=['00','01','10','11'])
<BarContainer object of 4 artists>
2.2 基于噪声样本的期望
要进行基于噪声样本的期望计算,可以使用 tfq.layers.SampleExpectation
some_observables = [cirq.X(my_qubits[0]), cirq.Z(my_qubits[0]), 3.0 * cirq.Y(my_qubits[1]) + 1]
some_observables
[cirq.X(cirq.GridQubit(0, 0)),
cirq.Z(cirq.GridQubit(0, 0)),
cirq.PauliSum(cirq.LinearDict({frozenset({(cirq.GridQubit(0, 1), cirq.Y)}): (3+0j), frozenset(): (1+0j)}))]
通过从电路中采样计算无噪声期望估计
noiseless_sampled_expectation = tfq.layers.SampledExpectation(backend='noiseless')(
my_circuit, operators=some_observables, repetitions=10000
)
noiseless_sampled_expectation.numpy()
array([[-0.0066, -1. , 0.9892]], dtype=float32)
将它们与噪声版本进行比较
noisy_sampled_expectation = tfq.layers.SampledExpectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_sampled_expectation.numpy()
/tmpfs/src/tf_docs_env/lib/python3.9/site-packages/keras/src/initializers/initializers.py:120: UserWarning: The initializer RandomUniform is unseeded and being called multiple times, which will return identical values each time (even if the initializer is unseeded). Please update your code to provide a seed to the initializer, or avoid using the same initializer instance more than once.
warnings.warn(
array([[-0.0034 , -0.34820002, 0.97959995],
[-0.0118 , 0.0042 , 1.015 ]], dtype=float32)
你可以看到噪声对 \(\langle \psi | Z | \psi \rangle\) 精度产生了特别大的影响,其中 my_really_noisy_circuit 非常快地集中到 0。
2.3 噪声分析期望计算
进行噪声分析期望计算与上述几乎相同
noiseless_analytic_expectation = tfq.layers.Expectation(backend='noiseless')(
my_circuit, operators=some_observables
)
noiseless_analytic_expectation.numpy()
array([[ 1.9106853e-15, -1.0000000e+00, 1.0000002e+00]], dtype=float32)
noisy_analytic_expectation = tfq.layers.Expectation(backend='noisy')(
[my_noisy_circuit, my_really_noisy_circuit], operators=some_observables, repetitions=10000
)
noisy_analytic_expectation.numpy()
array([[ 1.9106853e-15, -3.3100003e-01, 1.0000000e+00],
[ 1.9106855e-15, 5.0000018e-03, 1.0000000e+00]], dtype=float32)
3. 混合模型和量子数据噪声
现在你已经在 TFQ 中实现了一些噪声电路模拟,你可以通过比较和对比它们的噪声与无噪声性能来试验噪声如何影响量子和混合量子经典模型。要查看模型或算法是否对噪声具有鲁棒性的一个好的初步检查是在类似于以下内容的电路范围去极化模型下进行测试
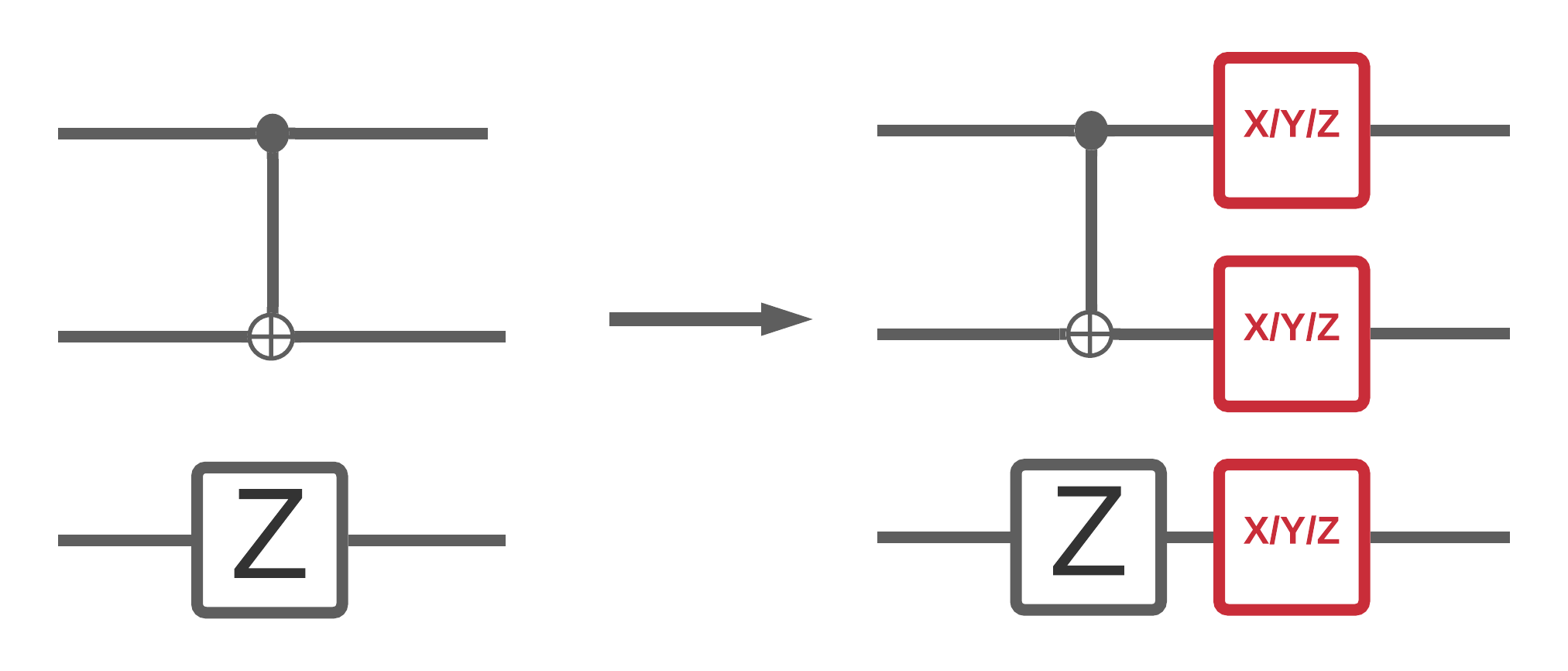
其中电路的每个时间切片(有时称为时刻)在该时间切片中的每个门操作后附加一个去极化通道。去极化通道将以概率 \(p\) 应用 \(\{X, Y, Z \}\) 之一或以概率 \(1-p\) 不应用任何操作(保留原始操作)。
3.1 数据
对于此示例,你可以在 tfq.datasets 模块中使用一些准备好的电路作为训练数据
qubits = cirq.GridQubit.rect(1, 8)
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
circuits[0]
Downloading data from https://storage.googleapis.com/download.tensorflow.org/data/quantum/spin_systems/XXZ_chain.zip 184449737/184449737 [==============================] - 2s 0us/step
编写一个小型帮助器函数将有助于为噪声与无噪声情况生成数据
def get_data(qubits, depolarize_p=0.):
"""Return quantum data circuits and labels in `tf.Tensor` form."""
circuits, labels, pauli_sums, _ = tfq.datasets.xxz_chain(qubits, 'closed')
if depolarize_p >= 1e-5:
circuits = [circuit.with_noise(cirq.depolarize(depolarize_p)) for circuit in circuits]
tmp = list(zip(circuits, labels))
random.shuffle(tmp)
circuits_tensor = tfq.convert_to_tensor([x[0] for x in tmp])
labels_tensor = tf.convert_to_tensor([x[1] for x in tmp])
return circuits_tensor, labels_tensor
3.2 定义模型电路
现在你以电路的形式获得了量子数据,你需要一个电路来对这些数据进行建模,就像使用数据一样,你可以编写一个帮助器函数来生成此电路,该电路可以选择性地包含噪声
def modelling_circuit(qubits, depth, depolarize_p=0.):
"""A simple classifier circuit."""
dim = len(qubits)
ret = cirq.Circuit(cirq.H.on_each(*qubits))
for i in range(depth):
# Entangle layer.
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[::2], qubits[1::2]))
ret += cirq.Circuit(cirq.CX(q1, q2) for (q1, q2) in zip(qubits[1::2], qubits[2::2]))
# Learnable rotation layer.
# i_params = sympy.symbols(f'layer-{i}-0:{dim}')
param = sympy.Symbol(f'layer-{i}')
single_qb = cirq.X
if i % 2 == 1:
single_qb = cirq.Y
ret += cirq.Circuit(single_qb(q) ** param for q in qubits)
if depolarize_p >= 1e-5:
ret = ret.with_noise(cirq.depolarize(depolarize_p))
return ret, [op(q) for q in qubits for op in [cirq.X, cirq.Y, cirq.Z]]
modelling_circuit(qubits, 3)[0]
3.3 模型构建和训练
在构建了数据和模型电路后,你需要的最后一个帮助器函数是能够组装一个噪声或无噪声混合量子 tf.keras.Model
def build_keras_model(qubits, depolarize_p=0.):
"""Prepare a noisy hybrid quantum classical Keras model."""
spin_input = tf.keras.Input(shape=(), dtype=tf.dtypes.string)
circuit_and_readout = modelling_circuit(qubits, 4, depolarize_p)
if depolarize_p >= 1e-5:
quantum_model = tfq.layers.NoisyPQC(*circuit_and_readout, sample_based=False, repetitions=10)(spin_input)
else:
quantum_model = tfq.layers.PQC(*circuit_and_readout)(spin_input)
intermediate = tf.keras.layers.Dense(4, activation='sigmoid')(quantum_model)
post_process = tf.keras.layers.Dense(1)(intermediate)
return tf.keras.Model(inputs=[spin_input], outputs=[post_process])
4. 比较性能
4.1 无噪声基准
使用你的数据生成和模型构建代码,你现在可以在无噪声和有噪声设置中比较和对比模型性能,首先你可以运行无噪声训练参考
training_histories = dict()
depolarize_p = 0.
n_epochs = 50
phase_classifier = build_keras_model(qubits, depolarize_p)
phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
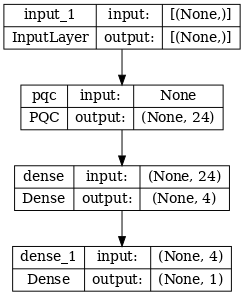
# Show the keras plot of the model
tf.keras.utils.plot_model(phase_classifier, show_shapes=True, dpi=70)
noiseless_data, noiseless_labels = get_data(qubits, depolarize_p)
training_histories['noiseless'] = phase_classifier.fit(x=noiseless_data,
y=noiseless_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 1s 129ms/step - loss: 0.6970 - accuracy: 0.4844 - val_loss: 0.6656 - val_accuracy: 0.4167 Epoch 2/50 4/4 [==============================] - 0s 62ms/step - loss: 0.6841 - accuracy: 0.4844 - val_loss: 0.6620 - val_accuracy: 0.4167 Epoch 3/50 4/4 [==============================] - 0s 66ms/step - loss: 0.6754 - accuracy: 0.4844 - val_loss: 0.6578 - val_accuracy: 0.4167 Epoch 4/50 4/4 [==============================] - 0s 62ms/step - loss: 0.6622 - accuracy: 0.4844 - val_loss: 0.6480 - val_accuracy: 0.4167 Epoch 5/50 4/4 [==============================] - 0s 63ms/step - loss: 0.6539 - accuracy: 0.4844 - val_loss: 0.6344 - val_accuracy: 0.4167 Epoch 6/50 4/4 [==============================] - 0s 62ms/step - loss: 0.6417 - accuracy: 0.4844 - val_loss: 0.6193 - val_accuracy: 0.4167 Epoch 7/50 4/4 [==============================] - 0s 61ms/step - loss: 0.6276 - accuracy: 0.4844 - val_loss: 0.6020 - val_accuracy: 0.4167 Epoch 8/50 4/4 [==============================] - 0s 60ms/step - loss: 0.6129 - accuracy: 0.4844 - val_loss: 0.5817 - val_accuracy: 0.4167 Epoch 9/50 4/4 [==============================] - 0s 61ms/step - loss: 0.5952 - accuracy: 0.5000 - val_loss: 0.5595 - val_accuracy: 0.6667 Epoch 10/50 4/4 [==============================] - 0s 60ms/step - loss: 0.5758 - accuracy: 0.6250 - val_loss: 0.5357 - val_accuracy: 0.7500 Epoch 11/50 4/4 [==============================] - 0s 61ms/step - loss: 0.5531 - accuracy: 0.6562 - val_loss: 0.5101 - val_accuracy: 0.9167 Epoch 12/50 4/4 [==============================] - 0s 59ms/step - loss: 0.5314 - accuracy: 0.7031 - val_loss: 0.4837 - val_accuracy: 0.9167 Epoch 13/50 4/4 [==============================] - 0s 59ms/step - loss: 0.5048 - accuracy: 0.7656 - val_loss: 0.4573 - val_accuracy: 0.9167 Epoch 14/50 4/4 [==============================] - 0s 59ms/step - loss: 0.4801 - accuracy: 0.7812 - val_loss: 0.4296 - val_accuracy: 0.9167 Epoch 15/50 4/4 [==============================] - 0s 61ms/step - loss: 0.4558 - accuracy: 0.7812 - val_loss: 0.4025 - val_accuracy: 0.9167 Epoch 16/50 4/4 [==============================] - 0s 60ms/step - loss: 0.4295 - accuracy: 0.8281 - val_loss: 0.3758 - val_accuracy: 0.9167 Epoch 17/50 4/4 [==============================] - 0s 59ms/step - loss: 0.4047 - accuracy: 0.8438 - val_loss: 0.3518 - val_accuracy: 1.0000 Epoch 18/50 4/4 [==============================] - 0s 60ms/step - loss: 0.3803 - accuracy: 0.8594 - val_loss: 0.3289 - val_accuracy: 1.0000 Epoch 19/50 4/4 [==============================] - 0s 61ms/step - loss: 0.3571 - accuracy: 0.8750 - val_loss: 0.3087 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 0s 60ms/step - loss: 0.3358 - accuracy: 0.9062 - val_loss: 0.2889 - val_accuracy: 1.0000 Epoch 21/50 4/4 [==============================] - 0s 60ms/step - loss: 0.3169 - accuracy: 0.9062 - val_loss: 0.2698 - val_accuracy: 1.0000 Epoch 22/50 4/4 [==============================] - 0s 60ms/step - loss: 0.2975 - accuracy: 0.9062 - val_loss: 0.2526 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 0s 60ms/step - loss: 0.2826 - accuracy: 0.9062 - val_loss: 0.2349 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 0s 59ms/step - loss: 0.2642 - accuracy: 0.9219 - val_loss: 0.2246 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 0s 60ms/step - loss: 0.2503 - accuracy: 0.9375 - val_loss: 0.2138 - val_accuracy: 1.0000 Epoch 26/50 4/4 [==============================] - 0s 60ms/step - loss: 0.2378 - accuracy: 0.9375 - val_loss: 0.2049 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 0s 59ms/step - loss: 0.2265 - accuracy: 0.9531 - val_loss: 0.1962 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 0s 59ms/step - loss: 0.2158 - accuracy: 0.9531 - val_loss: 0.1866 - val_accuracy: 1.0000 Epoch 29/50 4/4 [==============================] - 0s 59ms/step - loss: 0.2066 - accuracy: 0.9531 - val_loss: 0.1747 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 0s 60ms/step - loss: 0.1975 - accuracy: 0.9531 - val_loss: 0.1639 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1909 - accuracy: 0.9375 - val_loss: 0.1539 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1819 - accuracy: 0.9375 - val_loss: 0.1524 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1757 - accuracy: 0.9531 - val_loss: 0.1474 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1690 - accuracy: 0.9531 - val_loss: 0.1460 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 0s 58ms/step - loss: 0.1656 - accuracy: 0.9531 - val_loss: 0.1391 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1594 - accuracy: 0.9688 - val_loss: 0.1390 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1547 - accuracy: 0.9688 - val_loss: 0.1550 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 0s 60ms/step - loss: 0.1542 - accuracy: 0.9688 - val_loss: 0.1244 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1467 - accuracy: 0.9688 - val_loss: 0.1275 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 0s 60ms/step - loss: 0.1485 - accuracy: 0.9688 - val_loss: 0.1254 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1421 - accuracy: 0.9531 - val_loss: 0.1239 - val_accuracy: 1.0000 Epoch 42/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1453 - accuracy: 0.9844 - val_loss: 0.1243 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1333 - accuracy: 0.9844 - val_loss: 0.1065 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 0s 58ms/step - loss: 0.1361 - accuracy: 0.9375 - val_loss: 0.0930 - val_accuracy: 1.0000 Epoch 45/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1303 - accuracy: 0.9531 - val_loss: 0.1082 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 0s 60ms/step - loss: 0.1237 - accuracy: 0.9688 - val_loss: 0.1091 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1202 - accuracy: 0.9844 - val_loss: 0.1053 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1169 - accuracy: 0.9688 - val_loss: 0.0991 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 0s 59ms/step - loss: 0.1142 - accuracy: 0.9688 - val_loss: 0.0982 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 0s 61ms/step - loss: 0.1129 - accuracy: 0.9688 - val_loss: 0.1005 - val_accuracy: 1.0000
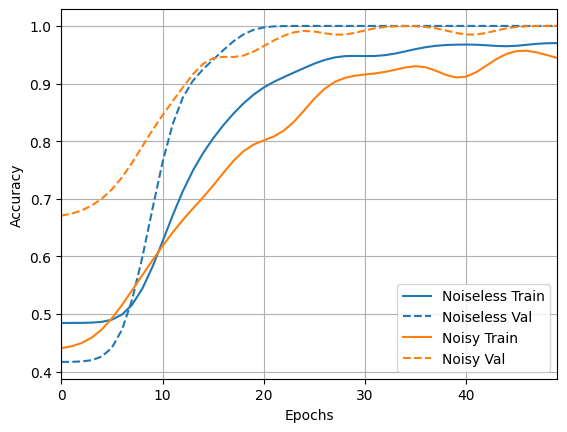
并探索结果和准确性
loss_plotter = tfdocs.plots.HistoryPlotter(metric = 'loss', smoothing_std=10)
loss_plotter.plot(training_histories)
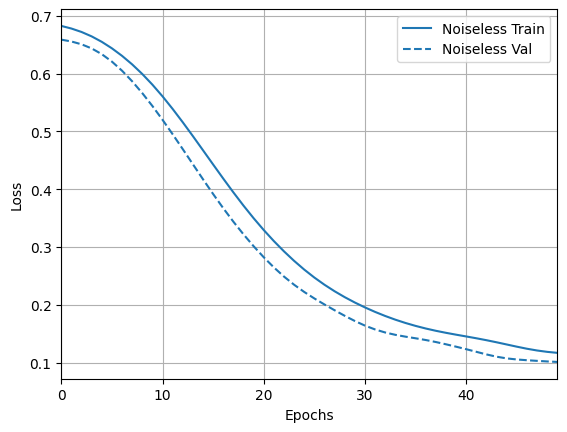
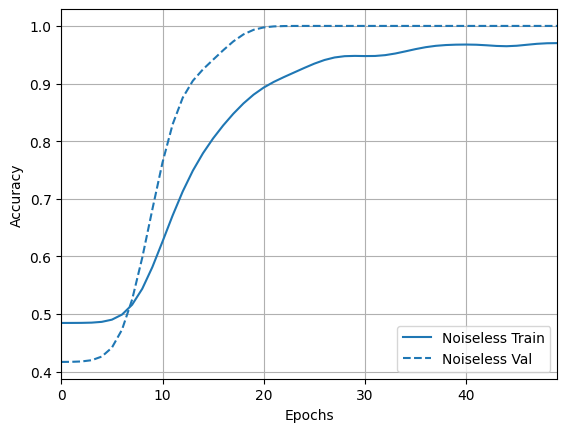
acc_plotter = tfdocs.plots.HistoryPlotter(metric = 'accuracy', smoothing_std=10)
acc_plotter.plot(training_histories)
4.2 有噪声比较
现在你可以构建一个带有噪声结构的新模型,并与上述模型进行比较,代码几乎相同
depolarize_p = 0.001
n_epochs = 50
noisy_phase_classifier = build_keras_model(qubits, depolarize_p)
noisy_phase_classifier.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.02),
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
# Show the keras plot of the model
tf.keras.utils.plot_model(noisy_phase_classifier, show_shapes=True, dpi=70)
noisy_data, noisy_labels = get_data(qubits, depolarize_p)
training_histories['noisy'] = noisy_phase_classifier.fit(x=noisy_data,
y=noisy_labels,
batch_size=16,
epochs=n_epochs,
validation_split=0.15,
verbose=1)
Epoch 1/50 4/4 [==============================] - 9s 1s/step - loss: 0.6851 - accuracy: 0.4375 - val_loss: 0.6770 - val_accuracy: 0.6667 Epoch 2/50 4/4 [==============================] - 5s 1s/step - loss: 0.6696 - accuracy: 0.4375 - val_loss: 0.6996 - val_accuracy: 0.6667 Epoch 3/50 4/4 [==============================] - 5s 1s/step - loss: 0.6609 - accuracy: 0.4375 - val_loss: 0.7085 - val_accuracy: 0.6667 Epoch 4/50 4/4 [==============================] - 5s 1s/step - loss: 0.6501 - accuracy: 0.4375 - val_loss: 0.7097 - val_accuracy: 0.6667 Epoch 5/50 4/4 [==============================] - 5s 1s/step - loss: 0.6461 - accuracy: 0.4844 - val_loss: 0.6984 - val_accuracy: 0.7500 Epoch 6/50 4/4 [==============================] - 5s 1s/step - loss: 0.6379 - accuracy: 0.4844 - val_loss: 0.6806 - val_accuracy: 0.6667 Epoch 7/50 4/4 [==============================] - 5s 1s/step - loss: 0.6281 - accuracy: 0.5156 - val_loss: 0.6689 - val_accuracy: 0.7500 Epoch 8/50 4/4 [==============================] - 5s 1s/step - loss: 0.6176 - accuracy: 0.5781 - val_loss: 0.6502 - val_accuracy: 0.7500 Epoch 9/50 4/4 [==============================] - 5s 1s/step - loss: 0.6082 - accuracy: 0.5938 - val_loss: 0.6304 - val_accuracy: 0.8333 Epoch 10/50 4/4 [==============================] - 5s 1s/step - loss: 0.5994 - accuracy: 0.5781 - val_loss: 0.6079 - val_accuracy: 0.8333 Epoch 11/50 4/4 [==============================] - 5s 1s/step - loss: 0.5889 - accuracy: 0.6250 - val_loss: 0.5922 - val_accuracy: 0.9167 Epoch 12/50 4/4 [==============================] - 5s 1s/step - loss: 0.5698 - accuracy: 0.6875 - val_loss: 0.5856 - val_accuracy: 0.8333 Epoch 13/50 4/4 [==============================] - 5s 1s/step - loss: 0.5624 - accuracy: 0.6875 - val_loss: 0.5666 - val_accuracy: 0.8333 Epoch 14/50 4/4 [==============================] - 5s 1s/step - loss: 0.5419 - accuracy: 0.6719 - val_loss: 0.5141 - val_accuracy: 1.0000 Epoch 15/50 4/4 [==============================] - 5s 1s/step - loss: 0.5321 - accuracy: 0.7188 - val_loss: 0.5024 - val_accuracy: 1.0000 Epoch 16/50 4/4 [==============================] - 5s 1s/step - loss: 0.5228 - accuracy: 0.6875 - val_loss: 0.4970 - val_accuracy: 1.0000 Epoch 17/50 4/4 [==============================] - 5s 1s/step - loss: 0.4946 - accuracy: 0.7812 - val_loss: 0.4924 - val_accuracy: 0.9167 Epoch 18/50 4/4 [==============================] - 5s 1s/step - loss: 0.4873 - accuracy: 0.7969 - val_loss: 0.4714 - val_accuracy: 0.8333 Epoch 19/50 4/4 [==============================] - 5s 1s/step - loss: 0.4708 - accuracy: 0.8281 - val_loss: 0.4329 - val_accuracy: 1.0000 Epoch 20/50 4/4 [==============================] - 5s 1s/step - loss: 0.4628 - accuracy: 0.7969 - val_loss: 0.3888 - val_accuracy: 1.0000 Epoch 21/50 4/4 [==============================] - 5s 1s/step - loss: 0.4419 - accuracy: 0.7969 - val_loss: 0.3807 - val_accuracy: 0.9167 Epoch 22/50 4/4 [==============================] - 5s 1s/step - loss: 0.4307 - accuracy: 0.7969 - val_loss: 0.3384 - val_accuracy: 1.0000 Epoch 23/50 4/4 [==============================] - 5s 1s/step - loss: 0.4010 - accuracy: 0.7969 - val_loss: 0.3665 - val_accuracy: 1.0000 Epoch 24/50 4/4 [==============================] - 5s 1s/step - loss: 0.3922 - accuracy: 0.8125 - val_loss: 0.3271 - val_accuracy: 1.0000 Epoch 25/50 4/4 [==============================] - 5s 1s/step - loss: 0.3638 - accuracy: 0.8906 - val_loss: 0.3407 - val_accuracy: 1.0000 Epoch 26/50 4/4 [==============================] - 5s 1s/step - loss: 0.3456 - accuracy: 0.9062 - val_loss: 0.2935 - val_accuracy: 1.0000 Epoch 27/50 4/4 [==============================] - 5s 1s/step - loss: 0.3580 - accuracy: 0.9219 - val_loss: 0.2527 - val_accuracy: 1.0000 Epoch 28/50 4/4 [==============================] - 5s 1s/step - loss: 0.3323 - accuracy: 0.9062 - val_loss: 0.3143 - val_accuracy: 0.9167 Epoch 29/50 4/4 [==============================] - 5s 1s/step - loss: 0.3380 - accuracy: 0.9062 - val_loss: 0.3100 - val_accuracy: 1.0000 Epoch 30/50 4/4 [==============================] - 5s 1s/step - loss: 0.2893 - accuracy: 0.9375 - val_loss: 0.2266 - val_accuracy: 1.0000 Epoch 31/50 4/4 [==============================] - 5s 1s/step - loss: 0.3008 - accuracy: 0.9062 - val_loss: 0.2205 - val_accuracy: 1.0000 Epoch 32/50 4/4 [==============================] - 5s 1s/step - loss: 0.2806 - accuracy: 0.9062 - val_loss: 0.2191 - val_accuracy: 1.0000 Epoch 33/50 4/4 [==============================] - 5s 1s/step - loss: 0.2657 - accuracy: 0.9219 - val_loss: 0.1817 - val_accuracy: 1.0000 Epoch 34/50 4/4 [==============================] - 5s 1s/step - loss: 0.2722 - accuracy: 0.9375 - val_loss: 0.2123 - val_accuracy: 1.0000 Epoch 35/50 4/4 [==============================] - 5s 1s/step - loss: 0.2790 - accuracy: 0.8906 - val_loss: 0.1979 - val_accuracy: 1.0000 Epoch 36/50 4/4 [==============================] - 5s 1s/step - loss: 0.2423 - accuracy: 0.9844 - val_loss: 0.2043 - val_accuracy: 1.0000 Epoch 37/50 4/4 [==============================] - 5s 1s/step - loss: 0.2493 - accuracy: 0.9688 - val_loss: 0.1863 - val_accuracy: 1.0000 Epoch 38/50 4/4 [==============================] - 5s 1s/step - loss: 0.2604 - accuracy: 0.8906 - val_loss: 0.1987 - val_accuracy: 1.0000 Epoch 39/50 4/4 [==============================] - 5s 1s/step - loss: 0.2329 - accuracy: 0.8906 - val_loss: 0.1580 - val_accuracy: 1.0000 Epoch 40/50 4/4 [==============================] - 5s 1s/step - loss: 0.2420 - accuracy: 0.8906 - val_loss: 0.1558 - val_accuracy: 1.0000 Epoch 41/50 4/4 [==============================] - 5s 1s/step - loss: 0.2384 - accuracy: 0.8750 - val_loss: 0.2039 - val_accuracy: 0.9167 Epoch 42/50 4/4 [==============================] - 5s 1s/step - loss: 0.2396 - accuracy: 0.9375 - val_loss: 0.1347 - val_accuracy: 1.0000 Epoch 43/50 4/4 [==============================] - 5s 1s/step - loss: 0.2038 - accuracy: 0.9531 - val_loss: 0.1266 - val_accuracy: 1.0000 Epoch 44/50 4/4 [==============================] - 5s 1s/step - loss: 0.2223 - accuracy: 0.9531 - val_loss: 0.1334 - val_accuracy: 1.0000 Epoch 45/50 4/4 [==============================] - 5s 1s/step - loss: 0.2050 - accuracy: 0.9688 - val_loss: 0.1155 - val_accuracy: 1.0000 Epoch 46/50 4/4 [==============================] - 5s 1s/step - loss: 0.1815 - accuracy: 0.9531 - val_loss: 0.1298 - val_accuracy: 1.0000 Epoch 47/50 4/4 [==============================] - 5s 1s/step - loss: 0.1666 - accuracy: 1.0000 - val_loss: 0.0986 - val_accuracy: 1.0000 Epoch 48/50 4/4 [==============================] - 5s 1s/step - loss: 0.1885 - accuracy: 0.9375 - val_loss: 0.0958 - val_accuracy: 1.0000 Epoch 49/50 4/4 [==============================] - 5s 1s/step - loss: 0.1865 - accuracy: 0.9219 - val_loss: 0.1410 - val_accuracy: 1.0000 Epoch 50/50 4/4 [==============================] - 5s 1s/step - loss: 0.1887 - accuracy: 0.9375 - val_loss: 0.1307 - val_accuracy: 1.0000
loss_plotter.plot(training_histories)
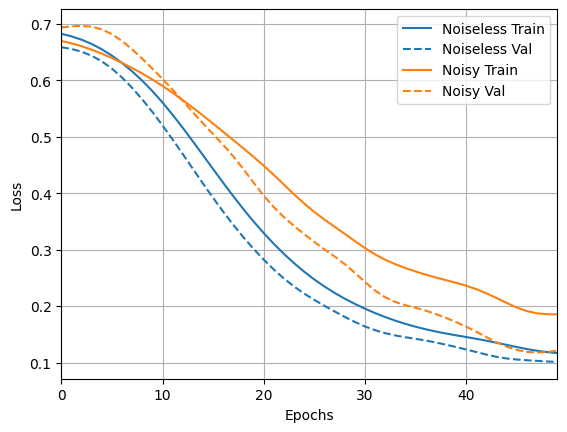
acc_plotter.plot(training_histories)