 在 TensorFlow.org 上查看 在 TensorFlow.org 上查看
|
 在 Google Colab 中运行 在 Google Colab 中运行
|
 在 GitHub 上查看源代码 在 GitHub 上查看源代码
|
 下载笔记本 下载笔记本
|
在此示例中,您将探索 McClean,2019 的结果,该结果表明并非任何量子神经网络结构在学习时都能表现良好。特别是,您将看到一定数量的随机量子电路组不能作为良好的量子神经网络,因为它们几乎在所有地方都具有消失的梯度。在此示例中,您不会针对特定学习问题训练任何模型,而是专注于理解梯度行为的更简单问题。
设置
pip install tensorflow==2.15.0
安装 TensorFlow Quantum
pip install tensorflow-quantum==0.7.3
# Update package resources to account for version changes.
import importlib, pkg_resources
importlib.reload(pkg_resources)
/tmpfs/tmp/ipykernel_20821/1875984233.py:2: DeprecationWarning: pkg_resources is deprecated as an API. See https://setuptools.pypa.io/en/latest/pkg_resources.html import importlib, pkg_resources <module 'pkg_resources' from '/tmpfs/src/tf_docs_env/lib/python3.9/site-packages/pkg_resources/__init__.py'>
现在导入 TensorFlow 和模块依赖项
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
np.random.seed(1234)
2024-05-18 11:31:46.453729: E external/local_xla/xla/stream_executor/cuda/cuda_dnn.cc:9261] Unable to register cuDNN factory: Attempting to register factory for plugin cuDNN when one has already been registered 2024-05-18 11:31:46.453776: E external/local_xla/xla/stream_executor/cuda/cuda_fft.cc:607] Unable to register cuFFT factory: Attempting to register factory for plugin cuFFT when one has already been registered 2024-05-18 11:31:46.455255: E external/local_xla/xla/stream_executor/cuda/cuda_blas.cc:1515] Unable to register cuBLAS factory: Attempting to register factory for plugin cuBLAS when one has already been registered 2024-05-18 11:31:49.800511: E external/local_xla/xla/stream_executor/cuda/cuda_driver.cc:274] failed call to cuInit: CUDA_ERROR_NO_DEVICE: no CUDA-capable device is detected
1. 摘要
具有许多类似于此类块的随机量子电路(\(R_{P}(\theta)\) 是随机泡利旋转)
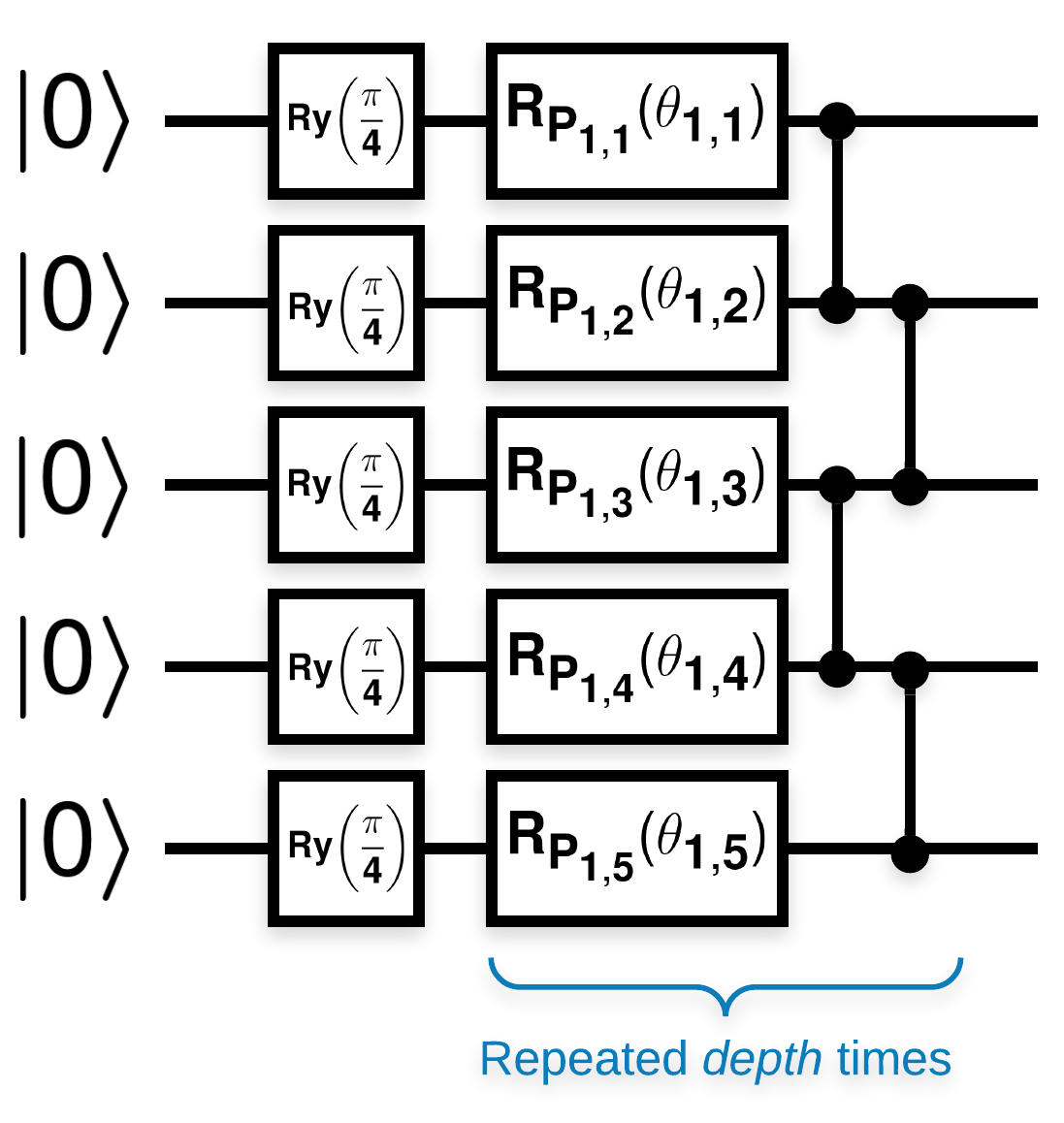
其中,如果将 \(f(x)\) 定义为关于任何量子位 \(a\) 和 \(b\) 的 \(Z_{a}Z_{b}\) 的期望值,则存在一个问题,即 \(f'(x)\) 的均值非常接近 0 且变化不大。您将在下面看到这一点
2. 生成随机电路
该论文中的结构很容易遵循。以下内容实现了一个简单的函数,该函数在给定一组量子位上的给定深度上生成随机量子电路(有时称为量子神经网络 (QNN))
def generate_random_qnn(qubits, symbol, depth):
"""Generate random QNN's with the same structure from McClean et al."""
circuit = cirq.Circuit()
for qubit in qubits:
circuit += cirq.ry(np.pi / 4.0)(qubit)
for d in range(depth):
# Add a series of single qubit rotations.
for i, qubit in enumerate(qubits):
random_n = np.random.uniform()
random_rot = np.random.uniform(
) * 2.0 * np.pi if i != 0 or d != 0 else symbol
if random_n > 2. / 3.:
# Add a Z.
circuit += cirq.rz(random_rot)(qubit)
elif random_n > 1. / 3.:
# Add a Y.
circuit += cirq.ry(random_rot)(qubit)
else:
# Add a X.
circuit += cirq.rx(random_rot)(qubit)
# Add CZ ladder.
for src, dest in zip(qubits, qubits[1:]):
circuit += cirq.CZ(src, dest)
return circuit
generate_random_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2)
作者研究了单个参数 \(\theta_{1,1}\) 的梯度。让我们通过在电路中放置一个 sympy.Symbol 来继续,其中 \(\theta_{1,1}\) 将存在。由于作者没有分析电路中任何其他符号的统计信息,因此现在让我们用随机值替换它们,而不是稍后替换。
3. 运行电路
生成一些此类电路以及一个可观察量,以测试梯度变化不大的说法。首先,生成一批随机电路。选择一个随机ZZ 可观察量,并使用 TensorFlow Quantum 批量计算梯度和方差。
3.1 批量方差计算
让我们编写一个帮助程序函数,该函数计算一批电路中给定可观测梯度的方差
def process_batch(circuits, symbol, op):
"""Compute the variance of a batch of expectations w.r.t. op on each circuit that
contains `symbol`. Note that this method sets up a new compute graph every time it is
called so it isn't as performant as possible."""
# Setup a simple layer to batch compute the expectation gradients.
expectation = tfq.layers.Expectation()
# Prep the inputs as tensors
circuit_tensor = tfq.convert_to_tensor(circuits)
values_tensor = tf.convert_to_tensor(
np.random.uniform(0, 2 * np.pi, (n_circuits, 1)).astype(np.float32))
# Use TensorFlow GradientTape to track gradients.
with tf.GradientTape() as g:
g.watch(values_tensor)
forward = expectation(circuit_tensor,
operators=op,
symbol_names=[symbol],
symbol_values=values_tensor)
# Return variance of gradients across all circuits.
grads = g.gradient(forward, values_tensor)
grad_var = tf.math.reduce_std(grads, axis=0)
return grad_var.numpy()[0]
3.1 设置并运行
选择要生成的随机电路的数量以及它们的深度和它们应该作用的量子比特数量。然后绘制结果。
n_qubits = [2 * i for i in range(2, 7)
] # Ranges studied in paper are between 2 and 24.
depth = 50 # Ranges studied in paper are between 50 and 500.
n_circuits = 200
theta_var = []
for n in n_qubits:
# Generate the random circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_random_qnn(qubits, symbol, depth) for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.title('Gradient Variance in QNNs')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:5 out of the last 5 calls to <function Adjoint.differentiate_analytic at 0x7f2a204ee4c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has reduce_retracing=True option that can avoid unnecessary retracing. For (3), please refer to https://tensorflowcn.cn/guide/function#controlling_retracing and https://tensorflowcn.cn/api_docs/python/tf/function for more details.
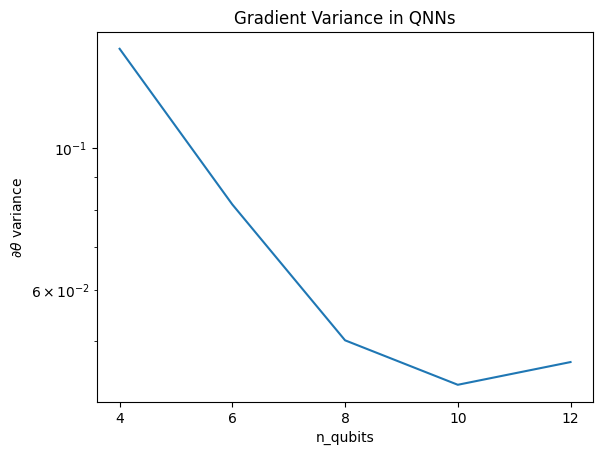
此图显示,对于量子机器学习问题,您不能简单地猜测一个随机 QNN ansatz 并寄希望于最好的结果。模型电路中必须存在某种结构,以便梯度变化到可以发生学习的程度。
4. 启发式
Grant, 2019 的一个有趣的启发式方法允许人们从非常接近随机开始,但又不完全是随机的。使用与 McClean 等人相同的电路,作者提出了一种不同的经典控制参数初始化技术,以避免贫瘠高原。初始化技术从完全随机的控制参数开始一些层,但在紧随其后的层中,选择参数,使得前几层做出的初始变换被撤消。作者称之为恒等块。
这种启发式方法的优点在于,只需更改一个参数,当前块之外的所有其他块都将保持恒等,并且梯度信号比以前强得多。这允许用户选择和修改哪些变量和块以获得强大的梯度信号。这种启发式方法并不能阻止用户在训练阶段陷入贫瘠高原(并限制完全同时更新),它只是保证您可以在高原之外开始。
4.1 新的 QNN 构造
现在构造一个函数来生成恒等块 QNN。此实现与论文中的实现略有不同。现在,观察单个参数的梯度行为,以便它与 McClean 等人的行为一致,因此可以进行一些简化。
要生成恒等块并训练模型,通常需要 \(U1(\theta_{1a}) U1(\theta_{1b})^{\dagger}\) 而不是 \(U1(\theta_1) U1(\theta_1)^{\dagger}\)。最初\(\theta_{1a}\) 和 \(\theta_{1b}\) 是相同的角度,但它们是独立学习的。否则,即使在训练后,您始终会得到恒等。恒等块数量的选择是经验性的。块越深,块中间的方差越小。但在块的开始和结束时,参数梯度的方差应该很大。
def generate_identity_qnn(qubits, symbol, block_depth, total_depth):
"""Generate random QNN's with the same structure from Grant et al."""
circuit = cirq.Circuit()
# Generate initial block with symbol.
prep_and_U = generate_random_qnn(qubits, symbol, block_depth)
circuit += prep_and_U
# Generate dagger of initial block without symbol.
U_dagger = (prep_and_U[1:])**-1
circuit += cirq.resolve_parameters(
U_dagger, param_resolver={symbol: np.random.uniform() * 2 * np.pi})
for d in range(total_depth - 1):
# Get a random QNN.
prep_and_U_circuit = generate_random_qnn(
qubits,
np.random.uniform() * 2 * np.pi, block_depth)
# Remove the state-prep component
U_circuit = prep_and_U_circuit[1:]
# Add U
circuit += U_circuit
# Add U^dagger
circuit += U_circuit**-1
return circuit
generate_identity_qnn(cirq.GridQubit.rect(1, 3), sympy.Symbol('theta'), 2, 2)
4.2 比较
在这里,您可以看到启发式方法确实有助于防止梯度的方差如此快地消失
block_depth = 10
total_depth = 5
heuristic_theta_var = []
for n in n_qubits:
# Generate the identity block circuits and observable for the given n.
qubits = cirq.GridQubit.rect(1, n)
symbol = sympy.Symbol('theta')
circuits = [
generate_identity_qnn(qubits, symbol, block_depth, total_depth)
for _ in range(n_circuits)
]
op = cirq.Z(qubits[0]) * cirq.Z(qubits[1])
heuristic_theta_var.append(process_batch(circuits, symbol, op))
plt.semilogy(n_qubits, theta_var)
plt.semilogy(n_qubits, heuristic_theta_var)
plt.title('Heuristic vs. Random')
plt.xlabel('n_qubits')
plt.xticks(n_qubits)
plt.ylabel('$\\partial \\theta$ variance')
plt.show()
WARNING:tensorflow:6 out of the last 6 calls to <function Adjoint.differentiate_analytic at 0x7f2a204ee4c0> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has reduce_retracing=True option that can avoid unnecessary retracing. For (3), please refer to https://tensorflowcn.cn/guide/function#controlling_retracing and https://tensorflowcn.cn/api_docs/python/tf/function for more details.
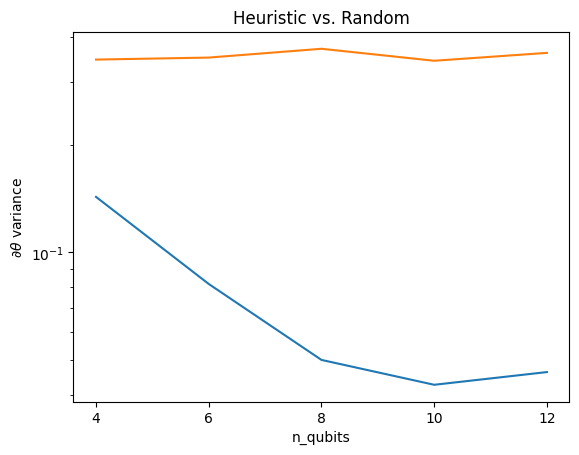
这是从(接近)随机 QNN 中获得更强梯度信号的一大改进。
